Отношения между понятиями

Рассуждая, человек совершает определенные действия с понятиями. Чтобы правильно оперировать понятиями, необходимо учитывать то обстоятельство, что понятия находятся в определенных отношениях между собой. Говорить об определенных отношениях мы можем только применительно к сравнимым понятиям.

Понятия сравнимы между собой, если их содержания имеют хотя бы один общий признак, т.е. такие понятия можно отнести к общему для них классу. Например, понятия "университет" и "школа" относятся к учебным заведениям. Если же в содержании понятий нет ни одного общего признака, то такие понятия называются несравнимыми. Например, "экономические отношения" и "кислота". Строго говоря несравнимость — вещь довольно условная. В конечном счете любые понятия можно подвести под одно общее понятие, т.е. найти в предметах, отраженных в этих понятиях, какие-то общие черты. Таким образом о несравнимости мы говорим в тех случаях, когда сходство между предметами не имеет значения. Среди несравнимых понятий не существует никаких отношений. Отношения между сравнимыми понятиями подразделяют на отношения совместимости и отношения несовместимости.

Понятия считаются совместимыми, если их объемы совпадают между собой либо полностью, либо частично, т.е. объемы этих понятий имеют общие элементы. Если же объемы понятий не имеют общих элементов, то такие понятия называются несовместимыми. Отношения между объемами понятий изображают при помощи специальных схем — кругов Эйлера, названных по имени Леонарда Эйлера (1707 - 1783) — швейцарского математика, физика и астронома.

Выделяют три типа совместимости: равнообъемность (равнозначность), перекрещивание (пересечение), подчинение.

Равнообъемными (равнозначными) считают такие понятия, которые имеют разное содержание, но объемы которых полностью совпадают. Например, "столица Республики Беларусь" (А) и "крупнейший промышленный центр Республики Беларусь" (В). Обратим внимание на то, что по содержанию это разные понятия, но объем у них один и тот же (рис. 2.1).

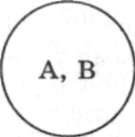
Рис. 2.1. Понятия А и В равнообъемны

Перекрещивающимися являются понятия, имеющие в своих объемах некоторые общие элементы, т.е. объемы этих понятий частично (но не полностью) совпадают. Например, "отец" и "брат"; "преподаватель экономической теории" и "преподаватель БГЭУ"; "международные отношения” и "торговля" (рис. 2.2).

______________

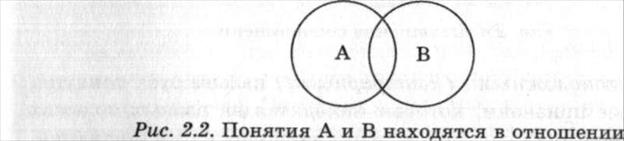
перекрещивания

Отношение подчинения характеризуется тем, что объем одного понятия (подчиненного) полностью входит в объем другого (подчиняющего), но не исчерпывает его, становится лишь его частью. Например, "лиственное дерево" (А) и "береза" (В) (рис. 2.3).

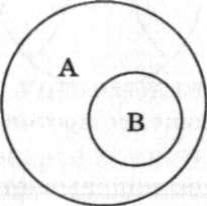
Рис. 2.3. Отношение подчинения

Если оба понятия, находящиеся в подобных отношениях, общие, то подчиняющее понятие называют еще родовым (родом), а подчиненное — видовым (видом). Отсюда еще одно название данного вида отношений — отношение рода и вида.

Отношения несовместимости подразделяются на отношения соподчинения, отношения противоречия и отношения противоположности.

В отношении соподчинения находятся такие понятия, которые являются видами одного рода, но объемы которых не имеют общих элементов. Например, понятия "тигр" (А) и "корова" (В) являются соподчиненными по отношению к понятию "животное"(С) (рис. 2.4).

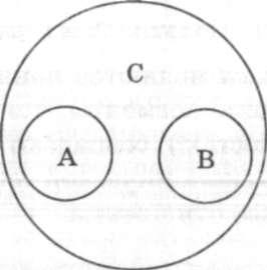
Рис. 2.4. Отношение соподчинения

Противоположными (контрарными) называются понятия, содержащие признаки, которые находятся на разных полюсах определенной шкалы оценок. Противоположными являются, например, такие понятия, как храбрость" и "трусость"; "самый молодой преподаватель вуза" и "самый

старый преподаватель вуза"; "богатый" и "бедный" (рис. 2.5).

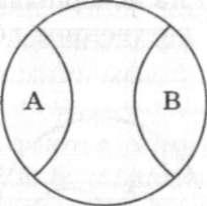
Рис. 2.5. Отношение противоположности

Данная схема наглядно показывает, что сумма объемов противоположных понятий не исчерпывает тот класс, видами которого они являются. Между этими крайними понятиями находятся еще определенные промежуточные понятия. Если обратиться к понятиям "самый молодой" и "самый старый", то мы видим, что между этими двумя крайностями можно расположить такие понятия, как "молодой", "человек среднего возраста", "пожилой", "старый". Не для всякого понятия можно подобрать противоположное понятие. Подобного рода отношения характерны прежде всего для понятий, выражающих оценочные характеристики. Попробуйте подобрать противоположное понятие, например, для таких понятий, как "стол", "дом" и т.п.

Противоречащими (контрадикторными) называют такие два несовместимых понятия, одно из которых отрицает признаки, составляющие содержание другого. Например, "женатый" — "холостяк" ("неженатый").

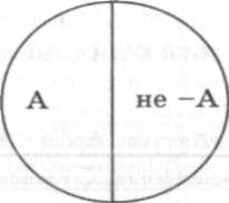
Рис. 2.6. Отношение противоречия

Сумма объемов противоречащих понятий равна объему универсального класса, т.е. того родового понятия, в объеме которого они мыслятся. Оппозиция "храбрость" — "нехрабрость", например, исчерпывает все морально-волевые состояния человека в отличие от оппозиции "храбрость" — "трусость".

Деление понятий

Деление понятия — это логическая операция, посредством которой объем делимого понятия (множество) распределяется на ряд подмножеств. В результате данной операции предметы, которые мыслятся в объеме исходного понятия, распределяются по группам. Например, углы в геометрии делят на острые, прямые и тупые. Эта операция имеет большое значение как для теоретической так и для практической деятельности человека. К ней прибегают, когда необходимо систематизировать какой-то материал, определить последовательность планируемых действий.

В процессе выработки понятий происходит обобщение предметов того или иного класса, т.е. отражаются некие общие для предметов данного класса признаки и игнорируются их видовые и индивидуальные особенности. Но дальнейшее развитие соответствующих знаний предполагает конкретизацию, выявление особенного в общем. Все это и достигается посредством операции деления.

В структуре операции деления различают: делимое понятие, члены деления, основание деления.

Делимым называется родовое понятие, объем которого подвергается делению, т.е. в объеме которого выделяют различные виды. Члены деления — это видовые понятия, получившиеся в результате деления. Основание деления— это признак, с учетом которого проводится деление.

Различают два вида деления понятия: деление по видоизменению признака и дихотомическое деление.

Деление по видоизменению признака — это такое деление, при котором каждый из членов деления включает в свой объем предметы, обладающие одним и тем же признаком, служащим основанием деления, но этот признак у предметов, принадлежащих разным членам деления, находит свое особое проявление; предметам каждой группы, выделенной в результате деления, данный признак присущ в различной степени. Например, всякое понятие можно характеризовать с точки зрения его объема. Но так как число элементов в объемах понятий может быть разным, принято деление понятий по объему на общие, единичные и пустые.

Если же при делении руководствоваться только наличием или отсутствием признака у предмета, то мы получим дихотомическое деление. В результате дихотомического деления объем понятия делится на два вида. Например, животных делят на млекопитающих и немлекопитающих; натуральные числа делятся на четные и нечетные.

Выполняя операцию деления понятия, необходимо выполнять следующие правила:

Правило 1.Деление должно производиться по одному основанию. Это означает, что признак, избранный в качестве основания деления, не должен в ходе деления подменяться другим признаком. При нарушении данного правила возникает ошибка "сбивчивое деление" или "деление не по одному основанию". Логически неправильно, например, делить обувь на мужскую, женскую и детскую (хотя именно так и подразделяют во многих магазинах отделы обуви). Данное правило касается однократной операции деления. Любое понятие можно делить по разным основаниям. Но всякий раз приступив к делению и избрав для этого определенное основание, следует придерживаться именно его.

Правило 2.Деление должно быть соразмерным, т.е. сумма объемов членов деления должна быть равна объему делимого понятия.При делении не должен оказаться пропущенным ни один предмет из объема делимого понятия и не должен появиться ни один лишний член деления, не входящий в объем делимого. При нарушении этого правила возможны два типа ошибок: "неполное деление", "деление с лишними членами". Деление будет неполным, если сумма объемов членов деления окажется частью объема делимого понятия. Например, "углы делят на острые и тупые". Названные члены деления не исчерпывают всего многообразия углов. В случаях, когда нет необходимости перечислять все члены деления, чтобы избежать данной ошибки, следует закончить фразу выражениями "и т.д.", "и т.п.", "и др.". Деление с лишними членами характеризуется тем, что объем делимого понятия оказывается лишь частью объединения объемов членов деления. Среди членов деления оказывается понятие, в котором мыслятся предметы, не входящие в объем делимого понятия. Например, "химические элементы делят на металлы, неметаллы и сплавы". В данном случае лишний член деления — понятие "сплавы", так как сплавы не являются химическими элементами.

Правило 3. Члены деления должны исключать друг друга. Это правило означает, что объемы членов деления не должны иметь общих элементов. Неправильно, например, делить страны на восточные, западные, северные и южные. (Правильно будет поделить страны в одном отношении на западные и восточные, а в другом отношении — на северные и южные). Нетрудно заметить связь этого правила с первым правилом: если деление производится не по одному основанию, то члены деления не исключают друг друга.

Правило 4. Деление должно быть непрерывным. (В литературе встречается еще одна формулировка этого правила: деление должно быть последовательным). Это означает, что от делимого родового понятия следует переходить к видовым понятиям одного и того же уровня, т.е. члены деления должны быть однопорядковыми видами по отношению к делимому понятию. При нарушении этого правила среди членов деления оказываются понятия, которые являются видовыми для делимого понятия и родовыми для других членов деления. Пример: "Предложения делятся на простые, сложносочиненные и сложноподчиненные." Правильно было бы поделить предложения на простые и сложные. А сложные, в свою очередь, можно было бы поделить на сложносочиненные и сложноподчиненные.

Многоступенчатое, разветвленное логическое деление, при котором каждый из членов, полученных в процессе этой операции, становится предметом дальнейшего деления, называется классификацией. Результатом классификации является система соподчиненных понятий: делимое понятие является родом, новые понятия — видами, видами видов (подвидами) и т.д.

Классическими примерами классификации, отражающими закономерные связи в определенной предметной области, являются периодическая система химических элементов Д.И.Менделеева и современная классификация (типология) живых существ.

Классификации играют большую роль как в научном познании, так и в практической деятельности людей. Классификация позволяет нам правильно ориентироваться в окружающем мире и принимать верные решения. Различают классификации естественные и искусственные. Если основанием деления был существенный признак, то полученная классификация будет называться естественной. Важной характеристикой естественной классификации является то, что в одну группу попадают объекты, объединенные большим количеством общих признаков. Искусственная классификация имеет своим основанием произвольно выбранные, случайные признаки. Деление книг в библиотеке по отраслям знаний представляет собой естественную их классификацию. Деление же книг по буквам фамилий их авторов является искусственной классификацией. Следует заметить, что противопоставление естественных и искусственных классификаций является в определенной мере относительным. То, что представляется несущественным в одном отношении, может оказаться существенным в другом. Если для социолога при выделении различных групп населения существенным будет социальное положение людей, их профессия и не существенным будет размер обуви, которую они носят, то для людей, планирующих массовое производство обуви и поэтому обеспокоенных проблемой соответствия спроса и предложения, последний признак (размер обуви) окажется одним из первостепенных.

Наряду с классификацией, существует еще один метод выделения подмножеств из определенного исходного множества. Это типологический метод. Типологиейназывают группировку объектов на основе их подобия некоторому образцовому предмету, который именуется типом. В качестве типа может рассматриваться как реально существующий объект (эталон), так

и мысленный образ (идеальный тип). Общеизвестным примером типологии является выделение Гиппократом следующих типов темперамента человека: сангвиник, холерик, флегматик и меланхолик. В соответствии с этой типологией каждый человек по своему темпераменту в большей или меньшей степени приближается к одному из этих типов. На практике далеко не всегда можно решить, к какому из указанных типов следует отнести того или иного человека. Этот пример указывает нам на одну из особенностей типологии: она, в отличие от классификации, не исключает того, что степень проявления каких-либо свойств делает проблематичным включение некоторого объекта в данную и только данную группу. Можно называть и еще одно отличие типологии от классификации: типология, в принципе, допускает, что среди группируемых объектов могут быть такие, которые не соответствуют ни одному из выделенных типов (атипичные объекты). С учетом названных особенностей типологию можно охарактеризовать как нестрогую (несовершенную, нежесткую) классификацию.

От рассмотренного выше логического деления следует отличать деление аналитическое (мериологическое). Если логическое деление базируется на отношении "род-вид", то аналитическое — на отношении "целое-часть". При логическом делении выявляют виды некоторого рода, а при аналитическом делении происходит мысленное вычленение в целом его частей или аспектов. Если, например, при логическом делении понятия "предложение" мы получаем видовые понятия "простое предложение", "сложное предложение", то применяя операцию аналитического деления, в предложении выделяют подлежащее, сказуемое и второстепенные члены. Частным случаем аналитического деления является периодизация — операция, при которой некий процесс подразделяют на этапы.