Свойства проецирования

Метод начертательной геометрии - метод проекций. Аппарат проецирования включает в себя проецирующие лучи, проецируемый объект(оригинал или прообраз)и плоскость проекций, на которой получается изображение объекта(проекция оригинала или образ) (рис.1.1).

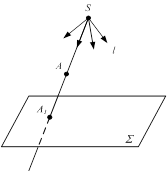
Различают три вида проецирования: центральное (а), параллельное (б) и ортогональное (перпендикулярное) (в). При центральном проецировании все лучи выходят из одной точки S (например, фотографирование).

Если центр проекций S удален в бесконечность, то все лучи становятся параллельными - параллельное проецирование.

Частный случай параллельного проецирования - ортогональное проецирование, когда проецирующие лучи перпендикулярны плоскости проекций.

а) б) в)

Σ - плоскость проекций; l - проецирующий луч; А - оригинал;

А₁ - проекция оригинала или точка пересечения проецирующего луча с плоскостью

Рисунок 1.1

Все виды проецирования обладают следующими свойствами:

1) Проекция точки есть точка (исключение - центр проекций S).

2) Проекция прямой есть прямая; частный случай - точка, если направление прямой совпадет с направлением проецирующего луча.

3) Если точка принадлежит прямой, то и проекция точки принадлежит проекции этой прямой.

Параллельное и ортогональное проецирование обладает кроме этого дополнительными свойствами:

4) Если прямые параллельны, то и их проекции параллельны.

5) Сохраняется величина отношения длин отрезков, лежащих на одной пря­мой или на параллельных прямых (рис.1.2а).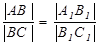

И, наконец, ортогональное проецирование обладает только ему присущими свойствами:

6) Для отрезка |АВ| и его ортогональной проекции |А₁В₁| справедливо соотношение (рис.1.2б): |А₁В₁ê=| АВ ê× соsj

где j - угол между отрезком и его ортогональной проекцией.

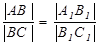
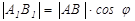
		ÐАВС=ÐА1В1С1=90°
а)	б)	в)

Рисунок 1.2

7) Прямой угол проецируется в прямой угол, если одна сторона прямого угла параллельна плоскости проекций, а вторая ей не перпендикулярна (рис.1.2 в).

Метод ортогонального проецирования лежит в основе изучаемого нами раздела начертательной геометрии. Однако, полученное изображение на одной плоскости проекций не позволяет однозначно определить форму и размеры изображенного предмета (рис.1.3).

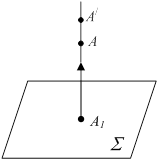
Рисунок 1.3