Отношение длины проекции аксонометрического единичного вектора к его натуральной длине называется коэффициентом искажения по соответствующей оси.

Коэффициенты искажения длины отрезка по аксонометрическим осям могут принимать различные значения:

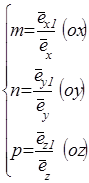
На практике используется три частных случая аксонометрических проекций: изометрия (m=n=p=0,82), диметрия (m=p=0,94; n =0,5m) и косоугольная диметрия (m=p=1; n=0,5).

Для упрощения в ЕСКД (единой системе конструкторской документации) приняты стандартные аксонометрические проекции с коэффициентами искажения и расположения осей приведенными на рис 1.6.

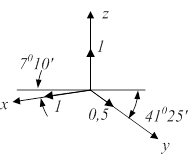
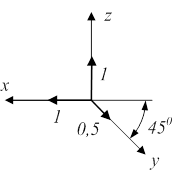
Изометрия M=n=p=1	Диметрия m=p=1; n=0,5	Косоугольная диметрия m=p=1; n=0,5

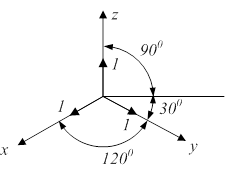
Рисунок 1.6

3) Комплексный чертеж или эпюр Монжа (основной способ начертательной геометрии, предложенный французским ученым Гаспаром Монжем)

Комплексный чертеж - чертеж, получаемый ортогональным проецированием на две взаимно перпендикулярные плоскости проекций. В пространстве фиксируются две взаимно перпендикулярные плоскости проекций: П1 ^ P₂ (рис. 1.7), на которые производим проецирование объекта.

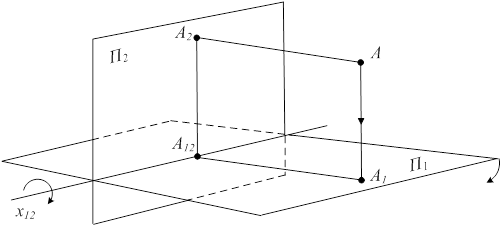
P₁ - горизонтальная плоскость проекций;

P₂ - фронтальная плоскость проекций;

x₁₂ - линия пересечения плоскостей проекций, ось чертежа;

А - оригинал (объект);

А₁ - горизонтальная проекция оригинала (точки А);

А₂ - фронтальная проекция оригинала (точки А).

Рисунок 1.7

Гаспар Монж предложил зафиксировать плоскость P₂, а P₁ вращать вокруг оси x₁₂ до совмещения с пл. P₂. От оригинала отказываемся, он остается в пространстве. Линия, соединяющая обе проек­ции А₁ и А₂ на чертеже, называется линией связи. Она всегда перпендикулярна оси чертежа x₁₂ (рис. 1.8). Получаем двухкартинный эпюр Монжа или комплексный чертеж.

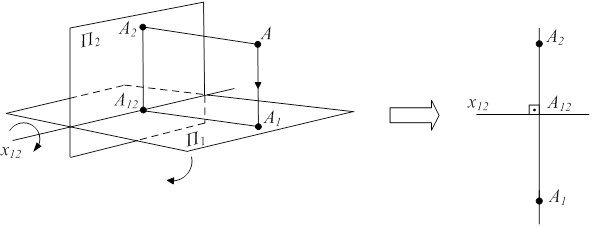
А₁ А₂ - линия связи; А₁ А₂ ^ x₁₂

Рисунок 1.8

Одновременное проецирование на две взаимно перпендикулярные плоскости проекций позволяет получить обратимый чертеж. Комплексный чертеж является чертежом обратимым.

êАА₁ê=|А₂ А₁₂ ê= r(АP₁) - расстояние от т. А до плоскости P₁ – высота.

êАА₂ê=êА₁А₁₂ ê= r(АP₂) - расстояние от т. А до плоскости P₂ – глубина.

Таким образом, по чертежу можно определить расстояния от точки А до плоскостей проекций, что говорит об обратимости комплексного чертежа.

Две проекции точки А₁ и А₂ на линии связи (А₁А₂ )^x₁₂ задают единственную точку А в пространстве.

Для наглядности и лучшего понимания, что такое комплексный чертеж, представим, что в точке А находится вершина трехгранной пирамиды S (S1S2 ^ x12); основание пирамиды D(АВС) лежит в плоскости P1 (рис.1.9); SА, SВ, SС – ребра пирамиды; r (от S2 до x12) – высота пирамиды; r (от S1 до x12) – глубина вершины пирамиды;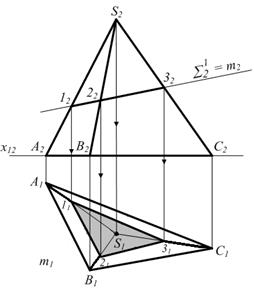

Рисунок 1.9

Условно плоскости проекций P₁ и P₂ делят пространство на четыре чет­верти (или квадранта) (рис. 1.10).

Т.к. плоскости проекций относительно объекта мы задаем сами, то удобнее всего оригинал (объект) располагать в первой четверти: над горизонтальной плоскостью проекций и перед фронтальной плоскостью проекций. Однако надо иметь в виду, что при решении конкретных задач прямые, плоскости или поверхности могут уйти за пределы первой четверти, во вторую, третью или четвертую четверти.

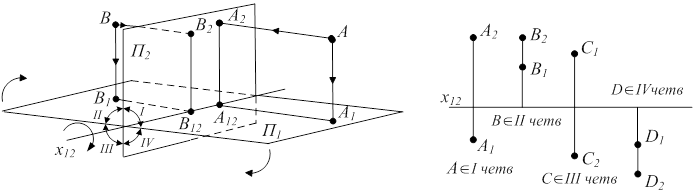
Рисунок 1.10