Наиболее важные законы распределения вероятностей в финансах.
2.1. Нормальный закон распределения.
Нормальный закон распределения (часто называемый законом Гаусса) играет исключительно важную роль в финансовых расчетах и занимает среди других законов распределения особое положение. Это - наиболее часто встречающийся в практике фондовой биржи закон распределения. Главная особенность, выделяющая нормальный закон среди других законов, состоит в том, что он является предельным законом, к которому приближаются другие законы распределения при весьма часто встречающихся типичных условиях.
Можно доказать, что сумма достаточно большого числа независимых (или слабо зависимых) случайных величин, подчиненных каким угодно законам распределения (при соблюдении некоторых весьма нежестких ограничений), приближенно подчиняется нормальному закону, и это выполняется тем точнее, чем большее количество случайных величин суммируется. Большинство встречающихся на практике случайных величин, таких, например, как изменение рыночной цены акции в течение торгового дня, колебания ежедневных объемов продаж какой-либо ценной бумаги, котируемой на бирже и т. д., могут быть представлены как суммы весьма большого числа сравнительно малых слагаемых - элементарных событий, каждая из которых вызвана действием отдельной причины, не зависящей от остальных. Каким бы законам распределения ни были подчинены отдельные элементарные события, особенности этих распределений в сумме большого числа слагаемых нивелируются, и сумма оказывается подчиненной закону, близкому к нормальному. Основное ограничение, налагаемое на суммируемые ошибки, состоит в том, чтобы они все равномерно играли в общей сумме относительно малую роль. Если это условие не выполняется и, например, одна из случайных ошибок окажется по своему влиянию на сумму резко превалирующей над всеми другими, то закон распределения этой превалирующей ошибки наложит свое влияние на сумму и определит в основных чертах ее закон распределения.
Нормальный закон распределения характеризуется плотностью вероятности вида:
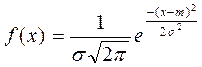 (2.1).
(2.1).
Кривая распределения по нормальному закону имеет симметричный холмообразный вид (рис. 2.1.).
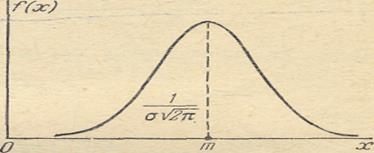
Рис. 2.1. Плотность нормального распределения.
Максимальная ордината кривой, равная 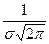 , соответствует точке х = m; по мере удаления от точки m плотность распределения падает, и при х, стремящемся к бесконечности, кривая асимптотически приближается к оси абсцисс.
, соответствует точке х = m; по мере удаления от точки m плотность распределения падает, и при х, стремящемся к бесконечности, кривая асимптотически приближается к оси абсцисс.
Выясним смысл численных параметров m и  , входящих в выражение нормального закона (2.1); можно доказать, что величина m есть не что
, входящих в выражение нормального закона (2.1); можно доказать, что величина m есть не что
иное, как математическое ожидание, а величина  - среднее квадратическое отклонение величины X. Непосредственно из формулы (2.1) видно, что центром симметрии распределения является центр рассеивания т. Это ясно из того, что при изменений знака разности(х - т) на обратный выражение (2.1) не меняется. Если изменять центр рассеивания т, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 2.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
- среднее квадратическое отклонение величины X. Непосредственно из формулы (2.1) видно, что центром симметрии распределения является центр рассеивания т. Это ясно из того, что при изменений знака разности(х - т) на обратный выражение (2.1) не меняется. Если изменять центр рассеивания т, кривая распределения будет смещаться вдоль оси абсцисс, не изменяя своей формы (рис. 2.2). Центр рассеивания характеризует положение распределения на оси абсцисс.
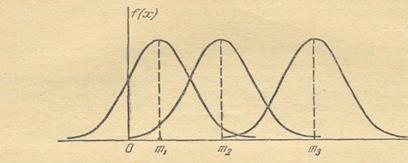
Рис. 2.2. Смещение кривой нормального распределения при изменении центра рассеивания.
Размерность центра рассеивания - та же, что размерность случайной величины X. Параметр  характеризует не положение, а саму форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна
характеризует не положение, а саму форму кривой распределения. Это есть характеристика рассеивания. Наибольшая ордината кривой распределения обратно пропорциональна  ; при увеличении
; при увеличении  максимальная ордината уменьшается. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении
максимальная ордината уменьшается. Так как площадь кривой распределения всегда должна оставаться равной единице, то при увеличении  кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении
кривая распределения становится более плоской, растягиваясь вдоль оси абсцисс; напротив, при уменьшении  кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 2.3 показаны три нормальные кривые (I, II, III) при m = 0; из них кривая I соответствует самому большому, а кривая III - самому малому значению
кривая распределения вытягивается вверх, одновременно сжимаясь с боков, и становится более иглообразной. На рис. 2.3 показаны три нормальные кривые (I, II, III) при m = 0; из них кривая I соответствует самому большому, а кривая III - самому малому значению  .
.
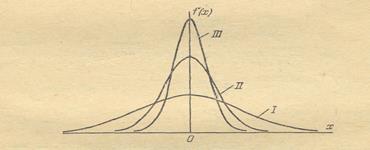
Рис. 2.3. Смещение формы кривой нормального распределения при изменении  .
.
Изменение параметра  равносильно изменению масштаба кривой распределения - увеличению масштаба по одной оси и такому же уменьшению по другой. Размерность параметра
равносильно изменению масштаба кривой распределения - увеличению масштаба по одной оси и такому же уменьшению по другой. Размерность параметра  , естественно, совпадает с размерностью случайной величины X.
, естественно, совпадает с размерностью случайной величины X.
Вероятность попадания случайной величины,
подчиненной нормальному закону, на заданный участок.
Нормальная функция распределения.
Во многих задачах, связанных с нормально распределенными случайными величинами, приходится определять вероятность попадания случайной величины X, подчиненной нормальному закону с параметрами т,  , на участок от
, на участок от 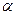 до
до 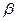 . Для вычисления этой вероятности воспользуемся общей формулой:
. Для вычисления этой вероятности воспользуемся общей формулой:
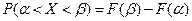 (2.2),
(2.2),
где F(х) - функция распределения величины Х.
Найдем функцию распределения F(х)случайной величины X, распределенной по нормальному закону с параметрами m,  . Плотность распределения величины X находится из выражения (2.1). Функцию же распределения можно найти следующим образом:
. Плотность распределения величины X находится из выражения (2.1). Функцию же распределения можно найти следующим образом:
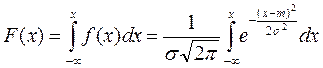 (2.3).
(2.3).
Сделаем в интеграле (2.3) замену переменной 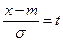 и приведем его к виду:
и приведем его к виду:
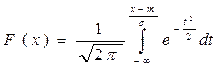 (2.4).
(2.4).
Интеграл (2.4) не выражается через элементарные функции, но его можно вычислить через специальную функцию, выражающую определенный интеграл от выражения 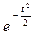 (так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функции, например:
(так называемый интеграл вероятностей), для которого составлены таблицы. Существует много разновидностей таких функции, например:
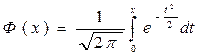 (2.5).
(2.5).
Нетрудно видеть, что эта функция представляет собой не что иное, как функцию распределения для нормально распределенной случайной величины с параметрами т = 0,  = 1.
= 1.
Условимся называть функцию Ф(х) нормальной функцией распределения. Во многих учебниках по статистике приведены таблицы значений функции Ф(х).
Выразим функцию распределения (2.3) величины X с параметрами m и  через нормальную функцию распределения Ф(x). Очевидно, что
через нормальную функцию распределения Ф(x). Очевидно, что
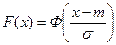 (2.6).
(2.6).
Теперь найдем вероятность попадания случайной величины X на  участок от
участок от 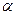 до
до 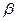 . Согласно формуле (2.2)
. Согласно формуле (2.2)
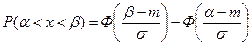 (2.7).
(2.7).
Таким образом, мы выразили вероятность попадания на участок случайной величины X, распределенной по нормальному закону с любыми параметрами, через стандартную функцию распределения Ф(х), соответствующую простейшему нормальному закону с параметрами (0, 1). Заметим, что аргументы функции Ф в формуле (2.7) имеют очень простой смысл: 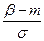 - есть расстояние от правого конца участка
- есть расстояние от правого конца участка 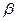 до центра рассеивания, выраженное в средних квадратических отклонениях;
до центра рассеивания, выраженное в средних квадратических отклонениях; 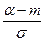 - такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания, и отрицательным, если слева.
- такое же расстояние для левого конца участка, причем это расстояние считается положительным, если конец расположен справа от центра рассеивания, и отрицательным, если слева.
Как и всякая функция распределения, функция Ф(х) обладает свойствами:
1. Ф( 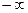 ) = 0.
) = 0.
2. Ф( 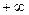 ) = 1.
) = 1.
3. Ф(х) - неубывающая функция.
Кроме того, из симметричности нормального распределения с параметрами m = 0,  = 1 относительно начала координат следует, что
= 1 относительно начала координат следует, что
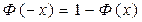 (2.8).
(2.8).
Пользуясь этим свойством можно было бы ограничить таблицы функции Ф(х) только положительными значениями аргумента, но, чтобы избежать лишней операции (вычитание из единицы), обычно в таблицах приводятся значения Ф(х)как для положительных, так и для отрицательных аргументов.
На практике часто встречается задача вычисления вероятности попадания нормально распределенной случайной величины на участок, симметричный относительно центра рассеивания т. Рассмотрим такой участок длины 2k(рис. 2.4). Вычислим вероятность попадания на этот участок по формуле (2.2):
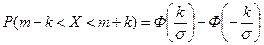 (2.9).
(2.9).
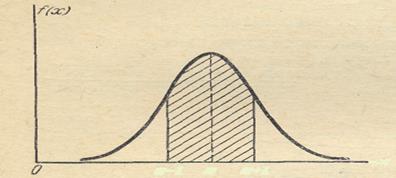
m-k m m+k x
Рис. 2.4. Расчет вероятности попадания нормально распределенной величины на участок 2k
Учитывая свойство (2.8) функции Ф(х) и придавая левой части формулы (2.9) более компактный вид, получим формулу для вероятности попадания случайной величины, распределенной по нормальному закону, на участок, симметричный относительно центра рассеивания:
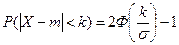 (2.10).
(2.10).
Решим следующую задачу. Отложим от центра рассеивания т последовательные отрезки длиной  (рис. 2.5) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.
(рис. 2.5) и вычислим вероятность попадания случайной величины X в каждый из них. Так как кривая нормального закона симметрична, достаточно отложить такие отрезки только в одну сторону.
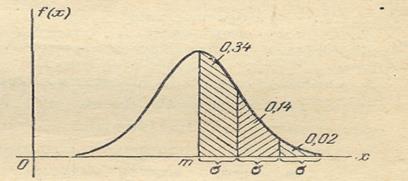
Рис. 2.5. Правило «трех сигма».
По формуле (2.7) находим:
Р (т < X < т +  ) = Ф(1) - Ф(0) = 0.8413 – 0.5 = 0.341;
) = Ф(1) - Ф(0) = 0.8413 – 0.5 = 0.341;
Р (т +  < X < т + 2
< X < т + 2  ) = Ф(2) - Ф(1) = 0.136;
) = Ф(2) - Ф(1) = 0.136;
Р (т + 2  < X < т + 3
< X < т + 3  ) = Ф(3) - Ф(2) = 0.012;
) = Ф(3) - Ф(2) = 0.012;
Р (т + 2  < X < т + 4
< X < т + 4  ) = Ф(4) - Ф(3) = 0.001.
) = Ф(4) - Ф(3) = 0.001.
Как видно из этих данных, вероятности попадания на каждый из следующих отрезков (пятый, шестой и т. д.) с точностью до 0,001 равны нулю. Округляя вероятности попадания в отрезки до 0,01 (до 1%), получим три числа, которые легко запомнить:
0.34; 0.14; 0.02.
Сумма этих трех значений равна 0.5. Это значит, что для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке т ± 3  .
.
Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математической статистике под названием «правило трех сигма». Из правила трех сигма вытекает также ориентировочный способ определения среднего квадратического отклонения случайной величины: берут максимальное практически возможное отклонение от среднего и делят его на три. Разумеется, этот грубый прием может быть рекомендован, только если нет других, более точных способов определения  .
.
 Для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке
Для нормально распределенной случайной величины все рассеивание (с точностью до долей процента) укладывается на участке 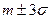 . Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математике под названием «правило трех сигма». Стандартное отклонение характеризует риск, связанный с данным активом. Чем больше величина отклонения, тем больше риск, и наоборот. Стандартное отклонение задается как процент отклонения цены актива от ее средней величины в расчете на год.
. Это позволяет, зная среднее квадратическое отклонение и математическое ожидание случайной величины, ориентировочно указать интервал ее практически возможных значений. Такой способ оценки диапазона возможных значений случайной величины известен в математике под названием «правило трех сигма». Стандартное отклонение характеризует риск, связанный с данным активом. Чем больше величина отклонения, тем больше риск, и наоборот. Стандартное отклонение задается как процент отклонения цены актива от ее средней величины в расчете на год.

 f(x)
f(x)

 68.3%
68.3%
 | |||
 |
 95.5%
95.5%





 99.7%
99.7%
-3 -2 -1 m 1 2 3 x
Рис. 2.6. Стандартное отклонение нормального распределения.
Например, если цена актива составляет 100 долл., а стандартное отклонение равно 10%, то это означает, что через год цена его может лежать в пределах от 90 долл. до 110 долл. в 68.3% случаев, от 80 долл. до 120 долл. в 95.4% случаях и от 70 долл. до 130 долл. в 99.7% случаях. Поскольку цена актива через год представляет собой результат действия рыночных сил, то она может и выйти за указанные пределы, однако в соответствии с кривой нормального распределения 99.7% всех вероятных исходов лежат в пределах трех стандартных отклонений от среднего значения показателя, 95.4% - в пределах двух стандартных отклонений и 68.3% - одного стандартного отклонения (см. рис. 2.6). Для того чтобы получить стандартное отклонение за период меньше года, необходимо стандартное отклонение в расчете на год разделить на квадратный корень из числа данных торговых периодов в году. Например, стандартное отклонение бумаги равно 10% в год, необходимо определить стандартное отклонение в расчете на день. В году насчитывается порядка 252 торговых дней. Поэтому стандартное отклонение за один день равно: 10% / 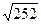 = 0.63%.
= 0.63%.
Пример: Доходность акции распределена нормально. Среднее значение доходности равно 20% годовых, стандартное отклонение доходности в расчете на год равно 10%. Определить с какой вероятностью через год доходность акций может оказаться в диапазоне от нуля до 40% ?
Ответ: 95.5% (см. рис. 2.6).
2.2. Распределение Пуассона.
Во многих задачах практики фондового рынка приходится иметь дело со случайными величинами, распределенными по своеобразному закону; который называется законом Пуассона.
Рассмотрим прерывную случайную величину X, которая может принимать только целые, неотрицательные значения: 0, 1, 2, ….m, …. причем последовательность этих значений теоретически не ограничена. Говорят, что случайная величина X распределена по закону Пуассона, если вероятность того, что она примет определенное значение m, выражается формулой
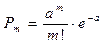 (m = 0, 1, 2, …) (2.11).
(m = 0, 1, 2, …) (2.11).
где а - некоторая положительная величина, называемая параметром закона Пуассона.
Убедимся, прежде всего, что последовательность вероятностей, задаваемая формулой (2.11), может представлять собой ряд распределения, т. е. что сумма всех вероятностей Рm равна единице. Имеем:
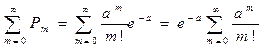 .
.
Но 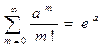 откуда
откуда 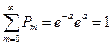 .
.
На рис. 2.7 показаны многоугольники распределения случайной величины X, распределенной по закону Пуассона, соответствующие различным значениям параметра а.
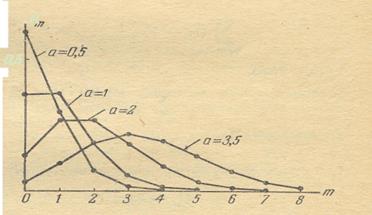
Рис. 2.7. Влияние параметра «а» на вероятность наступления события, распределенного по закону Пуассона.
Определим основные характеристики - математическое ожидание и дисперсию - случайной величины X, распределенной по закону Пуассона. По определению математического ожидания
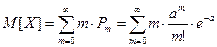
Первый член суммы (соответствующий т = 0) равен нулю, следовательно, суммирование можно начинать с m = 1:
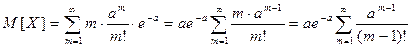
Обозначим (m – 1) = k; тогда
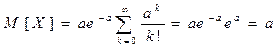
Таким образом, параметр а представляет собой не что иное, как математическое ожидание случайной величины X.
Для определения дисперсии найдем сначала второй начальный момент величины Х:
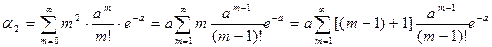 или далее
или далее
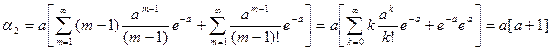
Далее, используя свойство дисперсии: 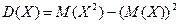 , получим:
, получим:
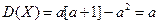 .
.
Таким образом, дисперсия случайной величины, распределенной по закону Пуассона, равна ее математическому ожиданию а.
Это свойство распределения Пуассона часто применяется на практике для решения вопроса, правдоподобна ли гипотеза о том, что случайная величина X распределена по закону Пуассона. Для этого определяют из опыта статистические характеристики (математическое ожидание и дисперсию) случайной величины. Если их значения близки, то это может служить доводом в пользу гипотезы о пуассоновском распределении; резкое различие этих характеристик, напротив, свидетельствует против гипотезы.
2.3. Логнормальное распределение.
Пусть S(t) - цена этой ценной бумаги в момент времени t и 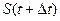 - цена в момент времени
- цена в момент времени 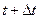 , тогда относительное изменение цены по истечении периода
, тогда относительное изменение цены по истечении периода 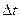 будет равно:
будет равно: 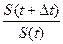 .
.
Предположим, что каждое из таких отношений цен на протяжении короткого отрезка времени 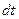 было случайной переменной, независимой и идентично распределенной. Тогда согласно центральной предельной теореме величины
было случайной переменной, независимой и идентично распределенной. Тогда согласно центральной предельной теореме величины 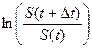 приблизительно нормально распределены. Центральная предельная теорема гласит, что если мы рассматриваем большую случайную выборку, то средняя величина ее будет нормально распределена. Таким образом, когда мы разделяем период времени на большое число промежутков (больше 30), с чем мы имеем дело, когда рассматриваем время как непрерывное, то сумма натуральных логарифмов будет нормально распределена.
приблизительно нормально распределены. Центральная предельная теорема гласит, что если мы рассматриваем большую случайную выборку, то средняя величина ее будет нормально распределена. Таким образом, когда мы разделяем период времени на большое число промежутков (больше 30), с чем мы имеем дело, когда рассматриваем время как непрерывное, то сумма натуральных логарифмов будет нормально распределена.
Переменная называется логнормально распределенной, если натуральный логарифм ее нормально распределен. Следовательно, если величина 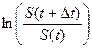 нормально распределена, то величина
нормально распределена, то величина 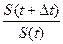 должна быть распределена логнормально.
должна быть распределена логнормально.
Это очень привлекательная модель распределения отношений цен ценных бумаг, потому что, если цена растет, то отношение цен будет больше единицы, если падает - то отношение цен будет меньше единицы, но оно никогда не принимает отрицательного значения. Теперь рассмотрим график функции логнормального распределения на рис. 2.8. На рисунке логнормальное распределение вытянуто вправо, но не имеет отрицательных значений. Это совместимо с возможным распределением цен ценных бумаг, поскольку они не могут упасть ниже нуля, и только очень немногие из наблюдений могли быть очень высоки.
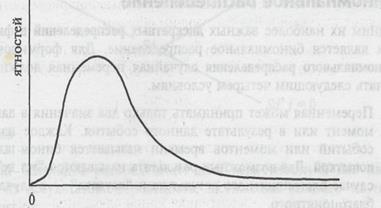
Рис. 2.8. Плотность вероятностей логнормального распределения.
Переменная не может принимать отрицательные значения, и вероятность очень высоких значений приближается к нулю, как это и можно ожидать от переменной, описывающей относительное изменение цены ценной бумаги. Логнормальное распределение очень часто используется для моделирования рыночных цен бумаг на фондовом рынке.
2.4. Математические приложения.
2.4.1. Матрицы.
Матрицей размера m на n называется прямоугольная таблица чисел, содержащая m строк и n столбцов. Числа, составляющие матрицу, называются элементами матрицы.
Матрицы обозначаются прописными (заглавными) буквами латинского алфавита, например, А, В, С. Для обозначения элементов матрицы используются строчные буквы с двойной индексацией: 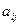 , где i – номер строки, j – номер столбца.
, где i – номер строки, j – номер столбца.
Виды матриц.Матрица, состоящая из одной строки, называется вектором-строкой, а из одного столбца – матрицей-столбцом. Матрица называется квадратной n-го порядка, если число ее строк равно числу столбцов и равно n. Например,
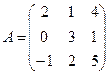 - квадратная матрица третьего порядка.
- квадратная матрица третьего порядка.
Элементы матрицы 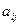 , у которой номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы
, у которой номер столбца равен номеру строки (i=j), называются диагональными и образуют главную диагональ матрицы. Для квадратной матрицы главную диагональ образуют элементы 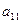 ,
, 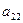 ,
, 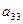 . Если все недиагональные элементы матрицы равны нулю, то матрица называется диагональной. Если у диагональной матрицы все диагональные элементы равны единице, то матрица называется единичной матрицей и обозначается буквой Е. Например,
. Если все недиагональные элементы матрицы равны нулю, то матрица называется диагональной. Если у диагональной матрицы все диагональные элементы равны единице, то матрица называется единичной матрицей и обозначается буквой Е. Например,
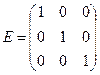 - единичная матрица третьего порядка.
- единичная матрица третьего порядка.
Матрица любого порядка называется нулевой, если все ее элементы равны нулю:
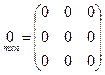 .
.
Операции над матрицами:
1. Умножение матрицы на число. Произведением матрицы А на число 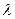 называется матрица
называется матрица 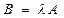 , элементы которой
, элементы которой 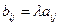 для i = 1, 2, … m; j = 1, 2, … n.
для i = 1, 2, … m; j = 1, 2, … n.
2. Сложение матриц. Суммой двух матриц А и В одинакового размера m на n называется матрица С = A + B, элементы которой 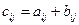 для i = 1, 2, … m; j = 1, 2, … n.
для i = 1, 2, … m; j = 1, 2, … n.
3. Умножение матриц. Умножение матрицы А на матрицу В определено, когда число столбцов первой матрицы равно числу строк второй. Тогда произведением матриц 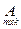 и
и 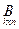 называется такая матрица
называется такая матрица 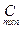 , каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
, каждый элемент которой равен сумме произведений элементов i-ой строки матрицы А на соответствующие элементы j-го столбца матрицы В.
Пример. Вычислить произведение матриц А и В, где
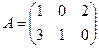 ;
; 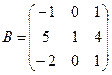 .
.
Ответ: 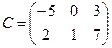 .
.
Пример. Найти произведения матриц А на В и В на А, где
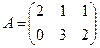 ;
; 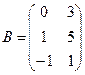 .
.
Ответ: 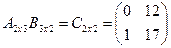 , а
, а 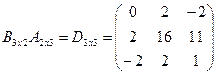 .
.
4. Транспонирование матрицы. Переход от матрицы А к матрице 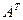 , в которой строки и столбцы поменялись местами с сохранением порядка, называется транспонированием матрицы. Матрица
, в которой строки и столбцы поменялись местами с сохранением порядка, называется транспонированием матрицы. Матрица 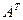 называется транспонированной относительно матрицы А, если:
называется транспонированной относительно матрицы А, если:
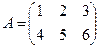 ;
; 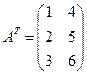 .
.
Дата добавления: 2017-10-04; просмотров: 2369;











