Вынужденные колебания в последовательном контуре

Рассмотрим вынужденные колебания в последовательном контуре, изображённом на рис. 2.21. Будем рассматривать случай установившихся колебаний, когда все переходные процессы закончились, то есть после включения источника напряжения прошло достаточно много времени t >> 1/δ .

Рис. 2.21. Последовательный колебательный контур, возбуждаемый генератором переменного напряжения и комплексная диаграмма напряжений на элементах контура на резонансной частоте.

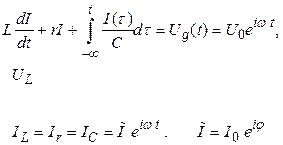Рассмотрим случай действия источника гармонических (синусоидальных) колебаний и напряжение источника запишем в комплексной форме U_g(t) = U₀ e^iωt. Тогда:

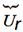(2.38)

Напряжения разные, а ток через элементы цепи одинаковый.

– комплексная величина. Она может быть сдвинута
по фазе относительно напряжения генератора.

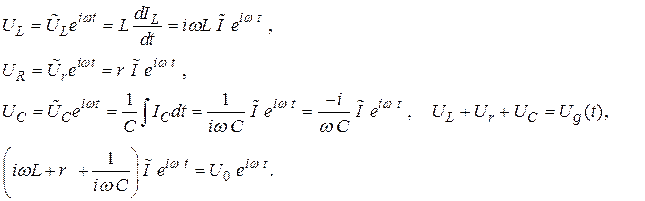
(2.39)

Здесь

где (2.40)

Здесь – импеданс последовательного колебательного контура, ξ – расстройка частоты, ρ – характеристическое или волновое сопротивление контура, Q – его добротность.

Физический смысл добротности Q будет рассмотрен ниже.

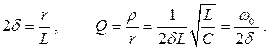
Кстати из (2.34): (2.41)

Физический смысл волнового сопротивления контура в том, что это – отношение максимального напряжения на конденсаторе (или на индуктивности) к максимальному току. Проще всего получить это выражение через равенство максимальных энергий, запасённых конденсатором и катушкой индуктивности.

Из (2.39) : (2.42)

(2.43)

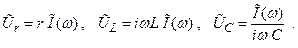Запишем комплексные амплитуды колебаний напряжений в виде:

(2.44)

Из (2.42): (2.45)

Это – сдвиг фаз между напряжением на контуре и током. Сдвиг фаз зависит от частоты.

Напряжение на сопротивлении не сдвинуто по фазе относительно тока:

Напряжение на индуктивности умножено на i (см. (2.44)), то есть

Напряжение на конденсаторе умножено на – i (2.44) и

См. диаграмму напряжений на рис. 2.21.

Ток через контур максимален на резонансе, при условии:

Если в (2.43)

Здесь ω₀ – резонансная частота, частота максимума тока.

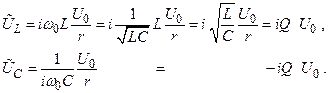На этой частоте напряжения на индуктивности и ёмкости равны и противофазны:

(2.46)

(2.47)

Сумма напряжений на ёмкости и индуктивности равна нулю на резонансной частоте, а импеданс контура минимален и равен r.

В этом случае фазы колебаний напряжений U_L и U_C таковы, что они компенсируют друг друга – это называется резонансом напряжений. Векторная диаграмма напряжений для этого случая приведена на рис. 2.21 справа.

На резонансе амплитуды напряжений U_L и U_C в Q раз больше напряжения генератора!

Если подавать на такой контур переменные напряжения с разными частотами, то контур будет выделять частоты, близкие к резонансной.

Напомним, что величина Q называется добротностью и для последовательного контура она равна отношению характеристического сопротивления ρ к сопротивлению .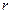

(2.48)

Рис. 2.22. Зависимости амплитуд вынужденных колебаний на ёмкости, сопротивлении и индуктивности для двух разных добротностей. При низкой добротности Q ~ 1 максимумы амплитуд разделяются. При добротностях Q >> 1 они почти совпадают. Напряжение на ёмкости при низкой частоте больше напряжения на индуктивности и равно напряжению на генераторе. На частотах выше резонансной напряжение больше на индуктивности. Соответственно изменится и вид векторной диаграммы на рис. 2.21. На максимумах напряжения на индуктивности и ёмкости равны и в Q-раз больше, чем напряжение на генераторе.

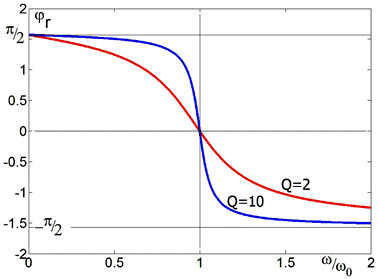
Рис. 2.23. Две фазовые характеристики, построенные по формуле (2.45) для разных добротностей. Это сдвиг фаз между напряжением на контуре и током.

Фазовые характеристики для напряжений на ёмкости и индуктивности просто сдвинуты вниз и вверх на π/2, см. (2.44).

Физический смысл добротности можно понять, если записать отношение запасённой в контуре энергии к энергии, теряемой за период.

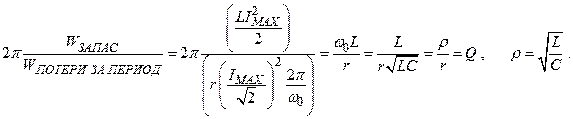
(2.49)

Последовательный контур можно использовать как полосовой фильтр, пропускающий частоты около резонанса. В радиоэлектронике принято характеризовать полосу граничными
частотами (на рис. 2.24 это частоты ω₁ и ω₂ ), при которых коэффициент передачи по модулю

падает до . Эти частоты определяются из уравнения:

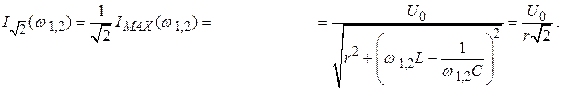
из ( 2.43)

Отсюда: (2.50)

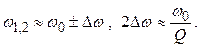
Решая уравнение (2.50), находим, что при Q >> 1 (2.51)

Заметим, что не каждому удаётся в уме решить даже квадратное уравнение и из (2.50) получить (2.51). Это решение приведено ниже. При первом чтении этот раздел можно пропустить.

Из (2.50)

Окончательно:

из (2.49):

(2.52)

если Q >> 1, то: (2.53)

Если Q << 1, то (2.52) лучше переписать в таком виде:

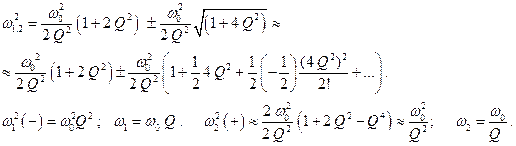
Сейчас пригодится третий член.

(2.54)

При выводе этой формулы пришлось учитывать и линейный, и квадратичный члены формулы бинома Ньютона.

Видим, что в случае малой добротности частоты ω₁ и ω₂ сильно различаются.

Величина добротности определяет полосу контура:

если Q >> 1, то или лучше (2.55)

Величину добротности контура по экспериментальной резонансной кривой можно вычислить, разделив резонансную частоту на ширину резонансной кривой на уровне 0.7.

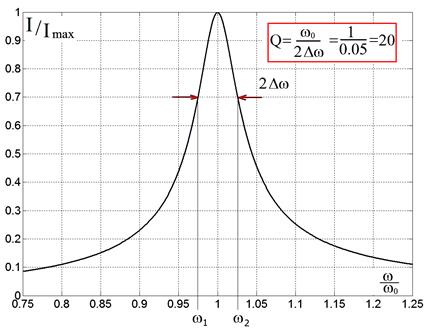
Рис. 2.24.

Резонанс тока в последовательном колебательном контуре с добротностью Q = 20.

График сосчитан по формуле (2.43) и нормирован на единицу.

Добротность, вычисленная по графику действительно равна 20!

Ток в последовательном контуре максимален на резонансной частоте. Значит, импеданс контура минимален на резонансе. На низких частотах импеданс емкостно́й, на высоких – индуктивный. На частоте, близкой к резонансной, его сопротивление минимальное и чисто омическое.