Энергетические процессы в резистивном, индуктивном и емкостном элементе

Мгновенная мощность в цепи с активным сопротивлением определяется произведением мгновенных значений напряжения и тока, т. е. .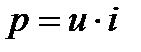

Рис. Изменение мощности в активном сопротивлении.

Мощность в цепи с ак­тивным сопротивлением изменяется по величине, но не изме­няется по направлению. Эта мощность (энергия) не­обратима. От источника она поступает потребителю и полно­стью преобразуется в другие виды мощности (энергии), т.е. потребляется. Такая потребляемая мощность называется актив­ной.

Поэтому и сопротивление R, на котором происходит подобное преобразование, называется активным сопротивлением.

В цепи с активным сопротивлением мгновенная мощность ха­рактеризует скорость преобразования электрической энергии в другие виды энергии.

Количественно мощность в цепи с активным сопротивлением определяется следующим образом:

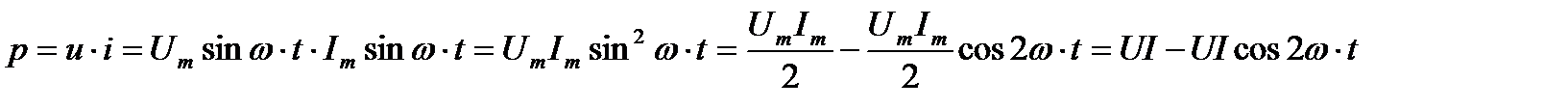
Мгновенная мощность в цепи синусоидального тока с активным сопротивлением представляет собой сумму двух величин - постоянной мощности UI и переменной 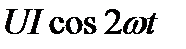, изменяющейся с двойной частотой.

Средняя за период мощность, равная постоянной составляю, щей мгновенной мощности UI, является активной мощностью P. Среднее за период значение переменной составляющей, как и всякой синусоидальной величины, равно нулю, то есть .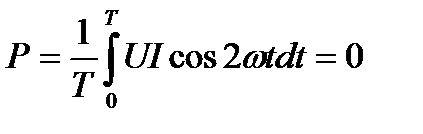

Таким образом, величина активной мощности в цепи синусои­дального тока с активным сопротивлением с учетом закона Ома определяется выражением:

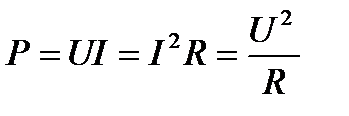
где U - действующее значение напряжения; I - действующее зна­чение тока.

Единицей активной мощности является ватт:

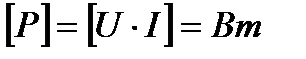
Мгновенная мощность для цепи синусоидального тока с идеа­льной катушкой равна произведению мгновенных значений на­пряжения и тока

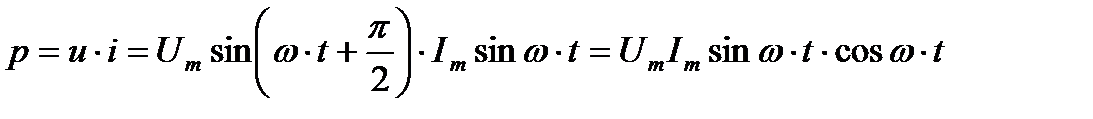
где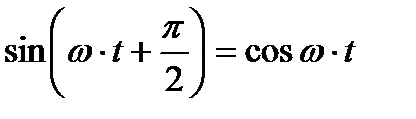

Следовательно, 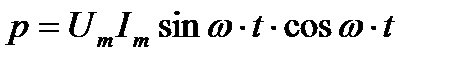. Полученное уравнение умножают и делят на 2:

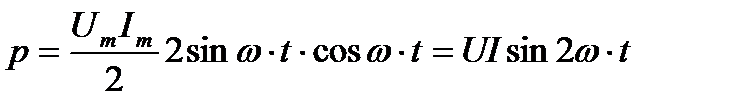
Таким образом, мощность в цепи синусоидального тока с идеаль­ной катушкой индуктивности изменяется по синусоидальному зако­ну с двойной частотой. То есть в 1-ю и 3-ю четверти периода мощность (энергия) ис­точника накапливается в магнитном поле индуктивности. Макси­мальное значение накапливаемой в магнитном поле идеальной катушки энергии равно

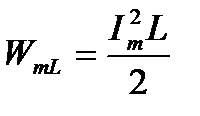
Во 2-ю и 4-ю четверти периода эта мощность (энергия) из маг­нитного поля идеальной катушки возвращается к источнику.

Рис. Изменение мощности в катушке индуктивности..

Следовательно, среднее значение этой мощности за период Р_С, как и любой синусоидальной величины, т. е. активная потребляе­мая мощность, в этой цепи равна нулю, Р = 0.

Таким образом, в цепи переменного тока с идеальной катушкой, мощность не потребляется (Р = 0), а колеблется между источ­ником и магнитным полем индуктивности, загружая источник и провода.

Такая колеблющаяся мощность (энергия), в отличие от активной, т. е. потребляемой, называется реактивной.

Обозначается реактивная мощность буквой Q и измеряется в варах, т.е. [Q] = вар (вольт-ампер реактивный).

Величина реактивной мощности в рассматриваемой цепи опре­деляется выражением

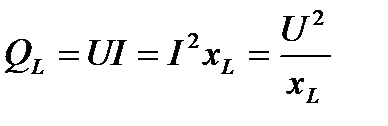
Так как реактивная мощность Q_L имеет место в цепи с индук­тивным сопротивлением, то индуктивное сопротивление считает­ся реактивным сопротивлением X индуктивного характера (ин­декс L), т.е. Х_L.

Если в цепи конденсатора емкостью С, R_C = 0 прохо­дит ток i, изменяющийся по синусоидальному закону:

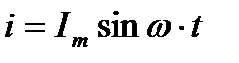
то напряжение u, приложенное к этому конденсатору, будет равно

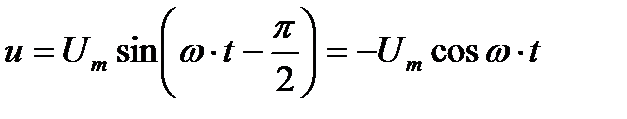
Мгновенная мощность в цепи с конденсатором

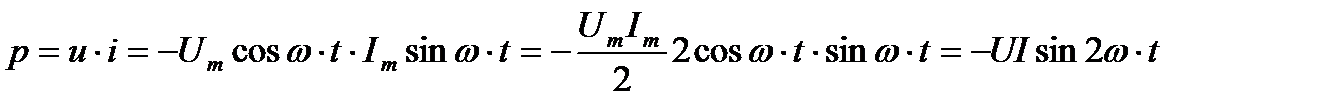
Мощность в цепи с конденсатором, подключенным к источнику с синусоидальным напряжением, изменяется по синусоидальному зако­ну с двойной частотой.

Следовательно, активная мощность Р в рассматриваемой цепи, равная среднему значению мгновенной мощности за период, имеет нулевое значение, Р = 0.

Во 2-ю и 4-ю четверти периода мощность (энергия) источника на­капливается в электрическом поле конденсатора.

Максимальное значение энергии, накапливаемой в электриче­ском поле конденсатора, равно

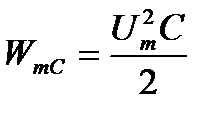
В 1-ю и 3-ю четверти периода эта мощность (энергия) из элект­рического поля конденсатора возвращается к источнику.

Рис. Изменение мощности в емкостном элементе.

Таким образом, в цепи переменного тока с конденсатором про­исходит колебание мощности (энергии) между источником и электрическим полем конденсатора.

Величина реактивной мощности в цепи конденсатора определя­ется выражением

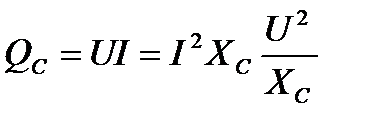
Реактив­ная мощность в цепи конденсатора изменяется в противофазе с реактивной мощностью в цепи с идеальной катушкой. Отсюда и знак «минус» в уравнении - аналитическом выражении мгновенной мощности в цепи с конденсатором.

Так как реактивная мощность Q_C имеет место в цепи с емкост­ным сопротивлением, то это емкостное сопротивление считается реактивным сопротивлением X емкостного характера (Х_C).

Полная мощность определяет эксплуатационные возможности многих электротехнических устройств. Связь между активной, реактивной и полной мощностью видно из выражения

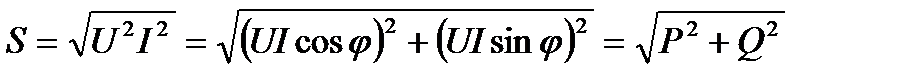
Она измеряется в вольт-амперах 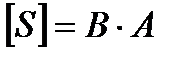. Величина полной мощности, равна произведению U·I, определяет основные габариты генераторов и трансформаторов. В самом деле, величина тока I определяет необходимое по условиям нагрева сечение проводов генераторов и трансформаторов, а число витков обмоток, их изоляция, а также размеры магнитопроводов пропорциональны величине напряжения U.

Таким образом, чем больше значения U и I, на которое рассчитаны генераторы и трансформаторы, тем больше должны быть их размеры.