Трехфазные цепи при синусоидальных напряжениях и токах. Соединение трех фаз в звезду и треугольник.

Трехфазные электротехнические устройства

Объединение в одну цепь нескольких подобных по структуре цепей синусоидального тока одной частоты с независимыми источниками энергии широко применяется в технике. Объединяемые цепи синусои­дального тока принято называть фазами, а всю объединенную систему цепей - многофазной системой. Таким образом, в электротехнике тер­мин «фаза» применяется в двух различных смыслах: во-первых, это параметр периодического процесса, а во-вторых, - наименование со­ставной части многофазной системы цепей синусоидального тока. Наи­большее распространение получила трехфазная система.

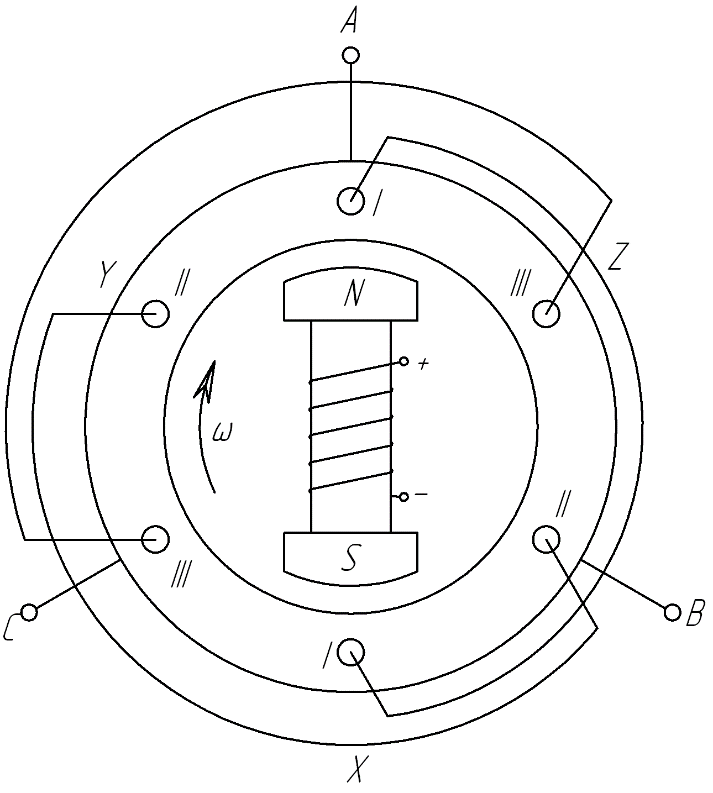
Источником энергии в трехфазной системе служит трехфазный гене­ратор. Он отличается от однофазного генератора синусоидального тока тем, что в пазах его статора размещены не одна, а три электрически изолированные друг от друга обмотки - фазные обмотки генератора. Если ротор генератора двухполюсный, то оси фаз­ных обмоток генератора повернуты в пространстве относительно друг друга на угол 2π/3 (рис. 3.1). При вращении ротора в фазных обмот­ках статора индуктируются синусоидальные фазные ЭДС. Вследствие симметрии конструкции генератора максимальные Е_m и действую­щие Е_ф значения ЭДС во всех фазах одинаковые. Однако линии маг­нитного поля вращающегося ротора пересекают провода фазных об­моток не одновременно. Поэтому синусоидальные ЭДС обмоток сдви­нуты по фазе относительно друг друга на одну треть периода, чему соответствует пространственный угол 2π/3 между осями обмоток.

Если ротор генератора многополюсный, то каждой паре его полю­сов соответствуют на статоре три изолированные друг от друга катушки трехфазных обмоток. Размещенные вдоль окружности статора отдель­ные катушки, число которых равно числу пар полюсов, каждой фаз­ной обмотки соединяются между собой последовательно или парал­лельно.

Фазы трехфазного генератора принято обозначать первыми бук­вами латинского алфавита: А, В, С. Последовательность в обозначе­нии фаз генератора, т. е. чередования фаз, не может быть случайной, так как она определяется последовательностью изменений во вре­мени фазных ЭДС. Обозначения выбираются так, чтобы ЭДС фазы А достигала максимального значения на одну треть периода раньше, чем ЭДС фазы В, и на две трети периода раньше, чем ЭДС фазы С.

Такая последовательность чередования фаз называется нормальной или прямой. От последовательности фаз зависит направление враще­ния трехфазных двигателей. При прямой последовательности чередо­вания фаз мгновенные значения ЭДС трех фазных обмоток симметрич­ного генератора равны:

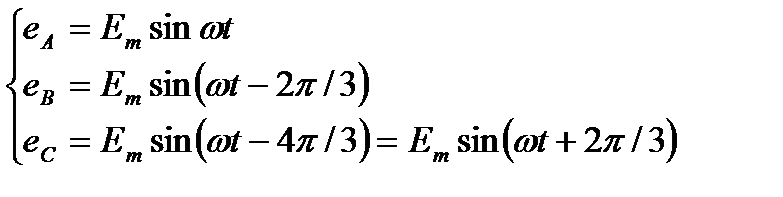(3.1)

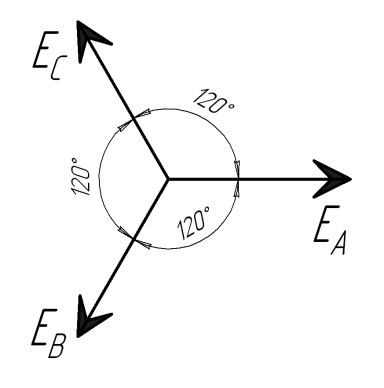
здесь с нулевой начальной фазой, как обычно, выбрана ЭДС фазы А.

На рис. 3.2 показаны график мгновенных значений фазных ЭДС и три вектора соответствующих им комплексных значений. Сумма трех векторов комплексных значений ЭДС равна нулю. Следовательно, алгебраическая сумма комплексных значений фазных ЭДС и алгебраи­ческая сумма мгновенных значений фазных ЭДС генератора равны нулю:

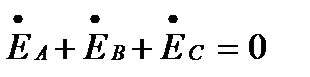(3.2а)

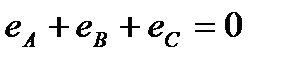(3.2б)

Комплексные значения ЭДС трехфазного симметричного генератора можно выразить через одинаковое для всех трех фаз действующее значение Е_Ф соответствующий комплексный множитель:

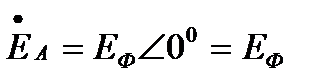
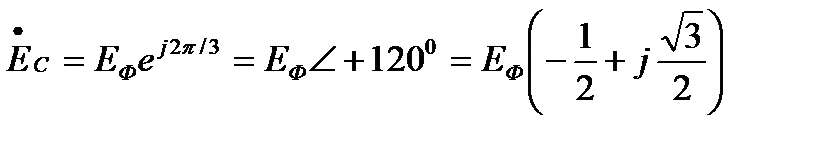
Комплексная величина 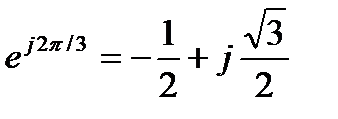называется фазным множителем трехфазной системы и обозначается буквой а. Умножение комплексного значения на а соответствует повороту изображаю­щего вектора на угол 2π/3 = 120° в положительном направлении, т. е. против направления движения стрелки часов. Таким образом,

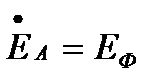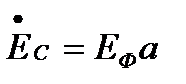; ; (3.3)

Для получения трехфазной системы необходимо определенным образом соединить фазы источника энергии и фазы приемника. Воз­можны два основных способа соединения в трехфазной системе - сое­динение источника энергии и приемника по схеме звезда и соединение источника энергии и приемника по схеме треугольник.

Соединение источника энергии и приемника по схеме звезда

Фазные обмотки трехфазного генератора можно соединить с тремя приемниками энергии шестью проводами и получить три неза­висимые фазные цепи. Необъединенная трехфазная система практически не применяется, но она важна для уяснения соотношений после объединения фазных цепей. Обратим внимание на стрелки, указываю­щие положительные направления фазных ЭДС. Эти положительные направления определяют «начала» (А, В, С) и «концы» (X, Y, Z) фаз­ных обмоток генератора.

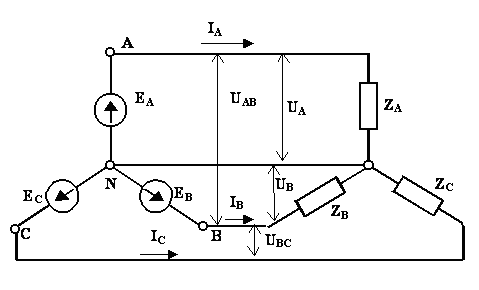
Рис. 3.4

У "источника энергии и приемника, выполненных по схеме звезда (условное обозначение Y), все концы фазных обмоток генератора сое­диняются в общий узел N (рис. 3.4); такой же узел n образует соединение трех фаз приемника, а три обратных провода фаз системы объединяются в один общий нейтральный провод. Остальные три провода, соединяющие генератор с приемником, называются линейными. Узел, который образуют обмотки фаз генератора или фазы приемника, называется нейтралью или нейтральной точкой.

Пренебрегая сопротивлениями всех проводов, легко определить токи трех фаз приемника и генератора:

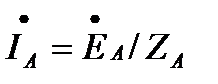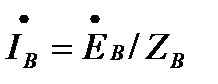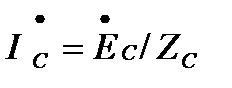; ; (3.4)

и ток в нейтральном проводе

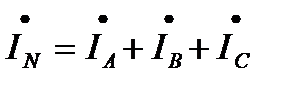(3.5)

Приемник с одинаковыми сопротивлениями всех трех фаз

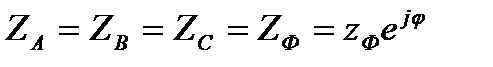
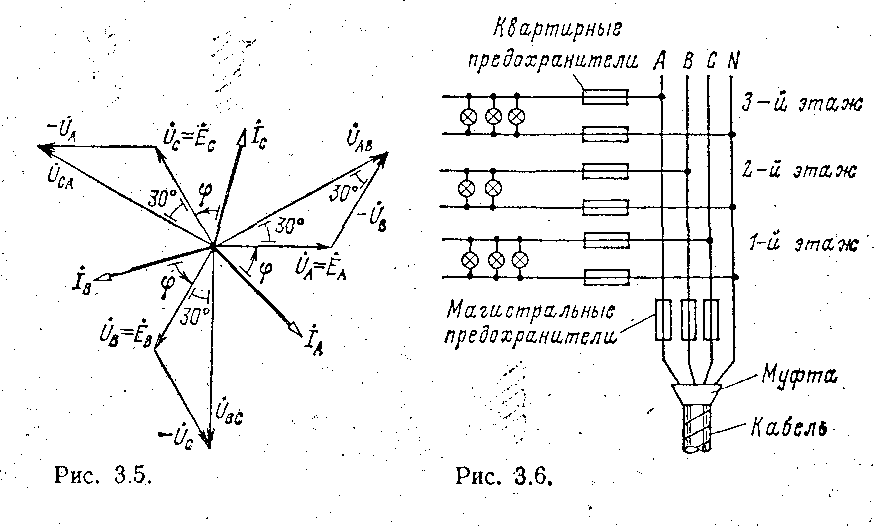
называется симметричным. При симметричном приемнике у токов всех фаз одинаковые действующие значения I_Ф и одинаковые сдвиги фаз φ относительно соответствующих фазных ЭДС (рис. 3.5), ток в нейтраль­ном проводе (3.5) равен нулю. Поэтому в случае симметрического при­емника, или, как говорят, при симметричной нагрузке генератора, нейтральный провод не нужен и не прокладывается. Примером такого приемника является трехфазный двигатель с соединением трехфаз­ных обмоток по схеме звезда.

В трехфазной системе напряжения , , 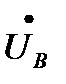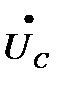между выводами каждой фазной обмотки генератора или каждой фазы приемника назы­ваются фазными напряжениями.

У симметричной трехфазной системы действующие значения фаз­ных напряжений одинаковы: .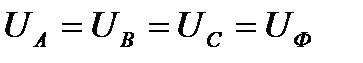

Фазными токами называются токи в фазных обмотках генератора или в фазах приемника. Напряжения между линейными проходами называются линейными и линейными называются токи в линейных проводах.

Запишем уравнения по второму закону Кирхгофа для контура, обозначенного на рис. 3.4 пунктиром, и двух других аналогичных кон­туров и учтем, что

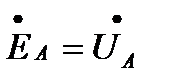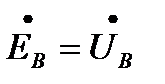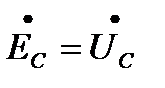; ; (3.6)

Для линейных напряжений получим:

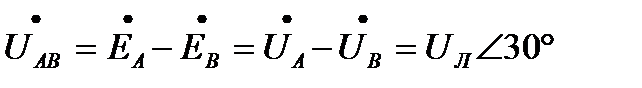(3.7а)

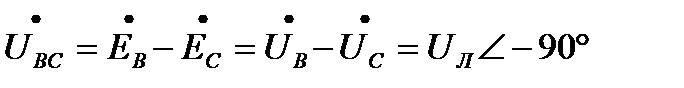(3.7б)

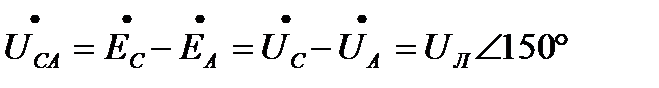(3.7в)

где U_Л - действующее значение линейного напряжения.

Векторная диаграмма фазных и линейных напряжений при соеди­нении источника энергии и приемника по схеме звезда дана на рис. 3.5. Вектор линейного напряжения 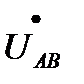построен по (3.7а), т. е. получен как результат суммирования вектора 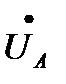и вектора 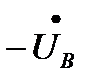который по длине равен вектору и противоположен ему по направлению. Аналогично построены и остальные два вектора линейных напря­жений.

При наличии нейтрального провода (рис. 3.4) условия (3.6) выпол­няются как при симметричном, так и при несимметричном приемнике, а при отсутствии нейтрального провода - только при симметричном. В обоих случаях векторы комплексных значений фазных и линейных напряжений образуют три одинаковых равнобедренных треугольника с углами 30° при основании. Из треугольников напряжений следует, что между действующими значениями линейных и фазных напряже­ний справедливо соотношение

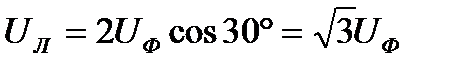(3.8)

Например, линейное напряжение U_Л = 380 В, а фазное U_Ф = 220 В или линейное U_Л = 220 В, а фазное U_Ф = 127 В.

При соединении источника энергии и приемника по схеме звезда линейные токи равны соответствующим фазным токам. В случае сим­метричного приемника действующие значения всех линейных и фазных токов одинаковые:

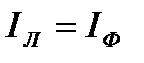(3.9)

Каждый трёхфазный двигатель представляет собой симметричный приемник. Поэтому для подключения электродвигателей к источнику энергии применяют трехпроводные линии. Но для осветительной на­грузки (рис. 3.6) нейтральный провод необходим, поскольку нет осно­ваний рассчитывать на полную симметрию такого трехфазного прием­ника. В нейтральном проводе четырехпроводной осветительной магистрали запрещена установка предохранителей или выключателей, так как при отключении нейтрального провода фазные напряжения могут стать неравными. В результате в одних фазах (или фазе) может наблюдаться недокал, а в других фазах (или фазе) - перекал и быстрое перегорание ламп. Если при таком соединении перегорит один из магистральных предохранителей, то отключатся лампы только одной (соответствующей) фазы.

Соединение источника энергии и приемника по схеме треугольника

У трехфазной системы, выполненной по схеме треугольник (услов­ное обозначение Δ), нейтральный провод отсутствует. Для получения из фаз­ных, обмоток генератора схемы треугольник (рис. 3.7, б) соединим ко­нец X первой обмотки с началом В второй обмотки, конец Y второй обмотки с началом С третьей обмотки и конец Z третьей обмотки с на­чалом А первой обмотки. Так как алгебраическая сумма синусоидаль­ных фазных ЭДС генератора равна нулю (3.2), то никакого дополни­тельного (уравнительного) тока в обмотках генератора не возникнет. Если фазные ЭДС отличаются от синусоидальных, то алгебраическая сумма ЭДС может и не равняться нулю, вследствие чего возникнет дополнительный ток в обмотках генератора. Это одна из причин отказа от соединения обмоток генера­торов по схеме треугольник.

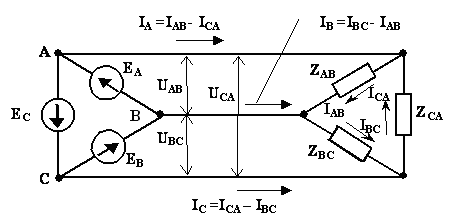
Рис. 3.7

После объединения обмоток генератора напряжения между началом и концом каждой фазы не изменятся, т. е. эти фазные напряжения оди­наковы для несвязанной и связанной (рис. 3.7, б) систем. Поэтому и токи в фазах приемника, т. е. фазные токи, 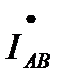, , 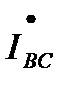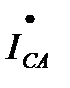в связанной системе такие же, как в несвязанной. Токи в каждом из трех объединенных линейных проводов, т. е. линейные токи, равны разностям соответствующих фазных токов (первый закон Кирхгофа для узлов приемника):

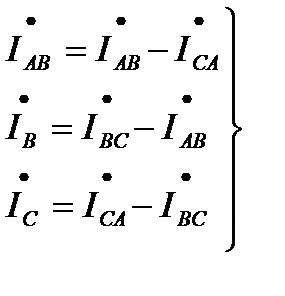(3.10)

Линейные напряжения равны соответствующим фазным напряжениям, их комплексные значения:

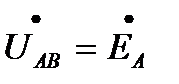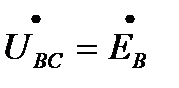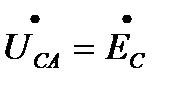; ; (3.11)

По закону Ома комплексные значения фазных токов:

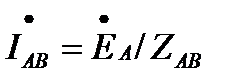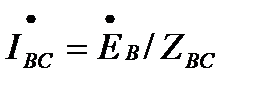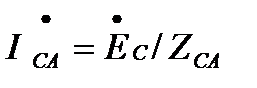; ; (3.12)

причем у симметричного приемника

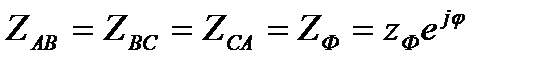(3.13)

и у всех фазных токов одинаковые действующие значения I_Ф и одина­ковые сдвиги фаз φ относительно соответствующих ЭДС или фазных напряжений.

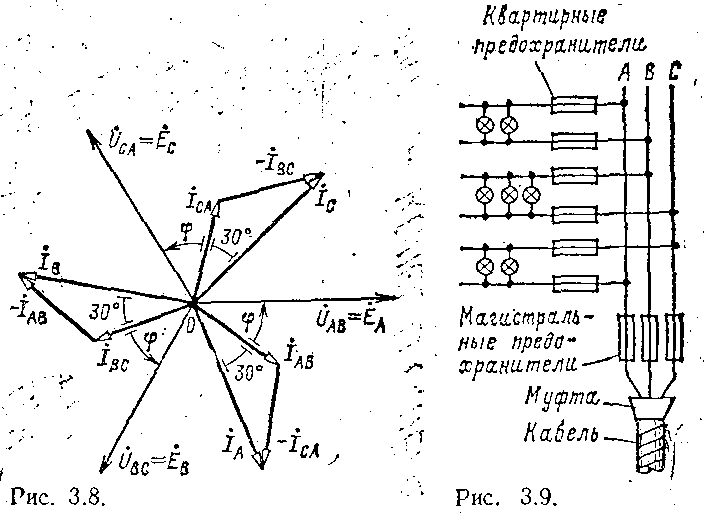
Векторная диаграмма напряжений и токов показана на рис. 3.8. Из треугольников токов следует, что в симметричной трехфазной си­стеме для действующих значений линейных и фазных токов справед­ливо соотношение

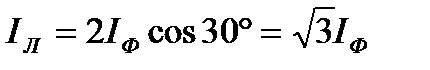(3.14)

Как следует из (3.11), действующие значения линейных и фазных напряжений равны друг другу и при несимметричном приемнике:

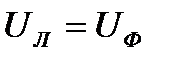(3.15)

Преимуществом соединения источника энергии и приемника по схеме треугольник по сравнению с соединением по схеме звезда без нейтрального провода является взаимная независимость фазных то­ков. На рис. 3.9 показана осветительная установка, выполненная по схеме треугольник. Если при таком соединении перегорит один из магистральных предохранителей (например, в линейном проводе В), то лампы в двух фазах (АВ и ВС) окажутся следовательно включен­ными и при одинаковой мощности ламп напряжение на лампах каждой из этих фаз будет равно только половине линейного (номинального) напряжения; напряжение на лампах третьей фазы {СА) останется нор­мальным.

Рассмотренные выше методы анализа соединений одноименных фаз источника энергии и приемника по схемам звезда и треугольник можно распространить и на трехфазную цепь, у которой схемы соеди­нения фаз источника энергии и фаз приемника различные.