Получение синусоидального напряжения и его параметры

Промышленными источникамисинусоидального тока являются электромеханические генераторы, в которых механическая энергия паровых и гидравлических турбин преобразуется в электрическую. Конструкция и работа промышленных электромеханических генераторов будет подробно рассмотрено в дальнейшем. Здесь же рассмотрим лишь принцип получения однофазного тока на упрощенной модели генератора, которая состоит из двух неподвижных магнитов и медной рамки вращающейся в воздушном пространстве между магнитами за счет приводного механизма с постоянной угловой частотой.

Пусть магнитный поток постоянного магнита равен Ф_m. Из пространственного расположения магнитного потока следует, что мгновенное значение составляющей магнитного потока, пронизывающей виток, т.е. направленной вдоль оси х, равно

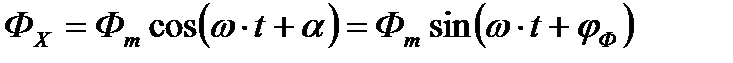(1)

где Ф_m – максимальное значение (амплитуда) магнитного потока, пронизывающего виток;

a - начальный (т.е. в момент t=0 принятый за начало отсчета времени) угол пространственного расположения постоянного магнита относительно оси х;

j_Ф - начальная фаза магнитного потока, ;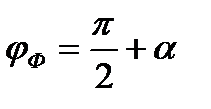

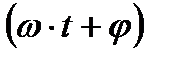- фаза магнитного потока. Здесь и в дальнейшем начальная фаза определяет значение синусоидальной величины в момент времени t=0.

Согласно закону электромагнитной индукции при изменении потокосцепления витка в нем индуцируется ЭДС

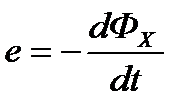
Подставляя сюда (1), имеем

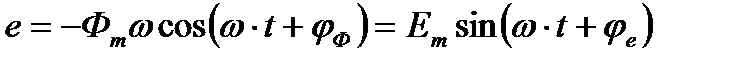
где 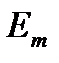- амплитуда ЭДС,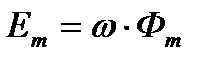

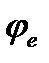- начальная фаза ЭДС,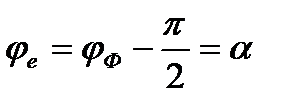

Синусоидальные величины принято изображать графически в виде зависимости 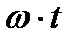. Поэтому начальная фаза определяет смещение синусоидальной величины относительно начала координат т.е. от .

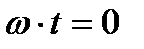Если начальная фаза >0, то начало синусоидальной величины сдвинуто влево, если <0, то – вправо от начала координат.

Если к выводам «а» и «в» генератора подключить резистор, то в полученной цепи возникнет синусоидальный ток i.

Пусть имеется однородное магнитное поле, образованное между полюсами N – S электромагнита. Внутри поля под действием посторонней силы вращается по окружности в сторону движения против часовой стрелки металлический прямолинейный проводник. Как известно, пересечение проводником магнитных линий приведет к появлению а проводнике индуцируемой ЭДС. 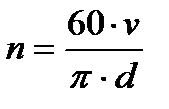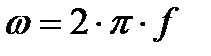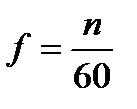Величина этой ЭДС зависит от величины магнитной индукции В, активной длины проводника l, скорости пересечения проводником магнитных линий v ( ; ; 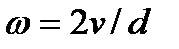) и синуса угла α между направлением движением проводника и направлением магнитного поля:

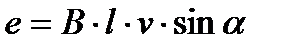
При движении проводник занимает различные положения при этом меняется значение угла, а в мести с ним и значение ЭДС, определяемое по правилу правой руки.

За один полный оборот проводника ЭДС в нем сначала увеличивается от нуля до максимального значения (E_m), а затем уменьшается до нуля и, изменив свое направление, вновь уменьшается до максимального значения (-E_m) и вновь уменьшается до нуля. При дальнейшем движении проводника указанные изменения ЭДС будут повторятся.

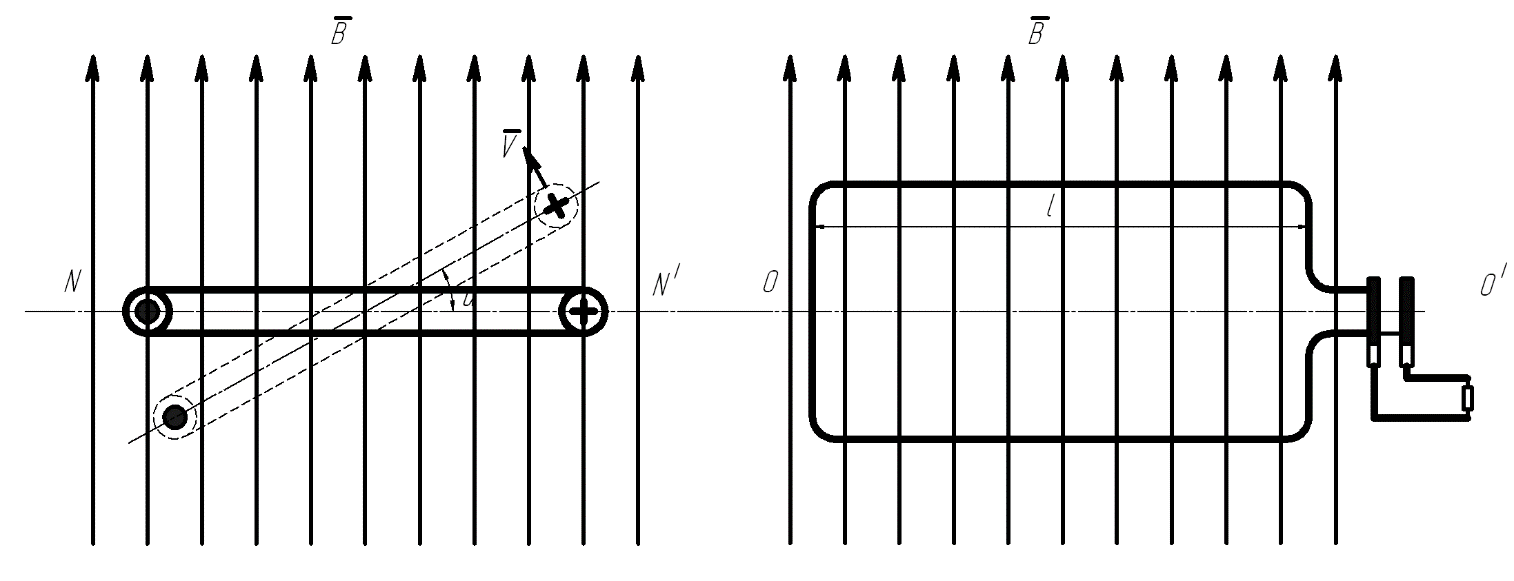
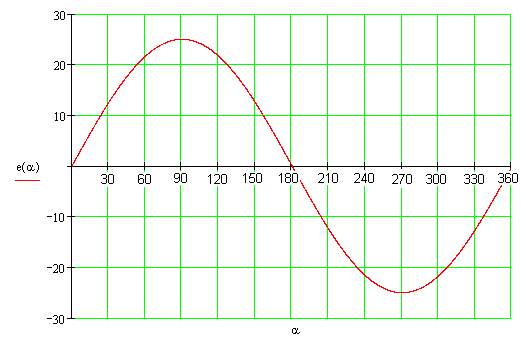
Рис. .

Амплитуда - это максимальное значение периодически изменя­ющейся величины.

Обозначаются амплитуды прописными буквами с индексом m, т. е. Е_m, U_m и I_m.

На основании рис. Можно сделать вывод, что ЭДС достигает своих амплитудных значений тогда, когда рамка повернется на угол α = 90° или на угол α = 270°, так как |sin 90°| = |sin 270°| = 1. Следовательно

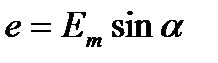(10.1)

Период - это время, в течение которого переменная величина делает полный цикл своих изменений, после чего изменения по­вторяются в той же последовательности.

Обозначается период буквой Т и измеряется в секундах, т.е. [Т] = с.

Частота - число периодов в единицу времени, т. е. величина, обратная периоду.

Обозначается частота буквой f, 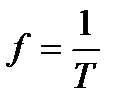, и измеряется в гер­цах (Гц):

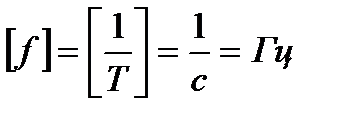
Стандартной частотой в электрических сетях России является частота f = 50 Гц. Для установок электронагрева пользуются частотами f = 50 ÷ 50·10⁶ Гц.

При частоте f = 50 Гц, т. е. 50 периодов в секунду, период

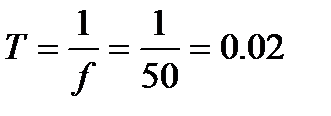c

Угловая частота (угловая скорость) характеризуется углом пово­рота рамки в единицу времени.

Обозначается угловая частота буквой ω (омега):

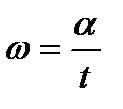(10.2)

Измеряется угловая частота в единицах радиан в секунду (рад/с), так как угол измеряется в радианах (рад).

За время одного периода Т рамка повернется на угол 360° = 2π рад. Следовательно, угловую частоту можно выразить следу­ющим образом:

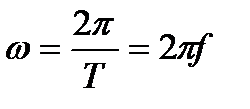(10.3)

Мгновенное значение - это значение переменной величины в любой конкретный момент времени.

Мгновенные значения обозначаются строчными буквами, т. е. e, i, u.

Из выражения (10.2) следует, что угол поворота рамки 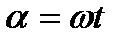, тогда мгновенные значения синусоидальных величин можно за­висать так:

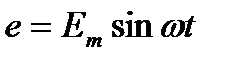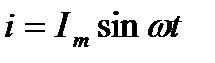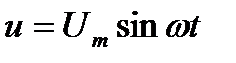; ; . (10.4)

Таким образом, любая синусоидальная величина характеризуется амплитудой и угловой частотой, которые являются постоянны­ми для данной синусоиды. Следовательно, по формулам (10.4) можно определить синусоидальную величину в любой конкретный момент времени t, если известны амплитуда и угловая частота.

Если в магнитном поле вращаются две жестко скрепленные между собой под каким-то углом одинаковые рамки (рис. 10.4а) т. е. амплитуды ЭДС Ет и угловые частоты со их одинаковы, то мгновенное значение их ЭДС можно записать в виде

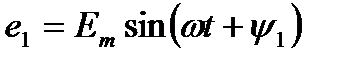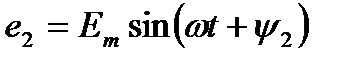; (10.5)

где ψ₁ и ψ₂ - углы, определяющие значения синусоидальных ве­личин е₁ и е₂ в начальный момент времени (t = 0), т. е.

;

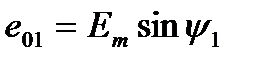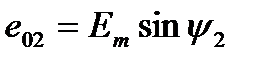
Поэтому эти углы ψ₁ и ψ₂ называют начальными фазамисину­соид.

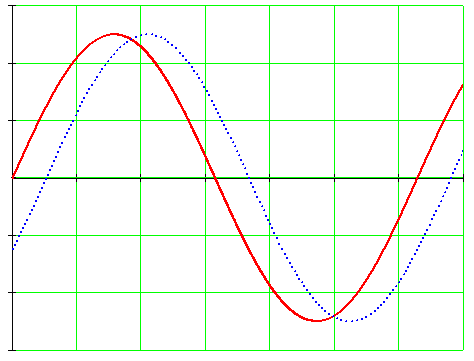
Рис. 10.4

Начальные фазы ψ₁ и ψ₂ этих ЭДС различны.

Таким образом, согласно (10.5) каждая синусоидальная величина характеризуется амплитудой Е_m, угловой частотой ω и начальной фазой ψ. Для каждой синусоиды эти величины (Е_m, ω и ψ) явля­ются постоянными. В выражениях (10.4) начальные фазы ψ сину­соид равны нулю.

Величина 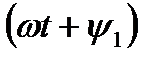называется фазой синусоиды.

Разность начальных фаз двух синусоидальных величин одинаковой частоты определяет угол сдвига фаз этих величин:

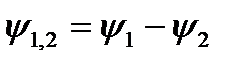(10.6)

При вращении против часовой стрелки (рис. 10.4а) ЭДС в первой рамке достигает амплитудного и нулевого значения раньше чем во второй, т. е. е₁ опережает по фазе е₂ или е₂ отстает по фазе от е₁ (рис. 10.46). Угол сдвига фаз 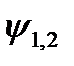показывает, на какой угол одна синусоидальная величина опережает или отстает от другой (т.е. достигает своих амплитудных и нулевых значений раньше или позже).

Две синусоидальные величины одинаковой частоты, достигаю­щие одновременно своих амплитудных (одного знака) и нулевых значений, считаются совпадающими по фазе (рис. 10.5а).

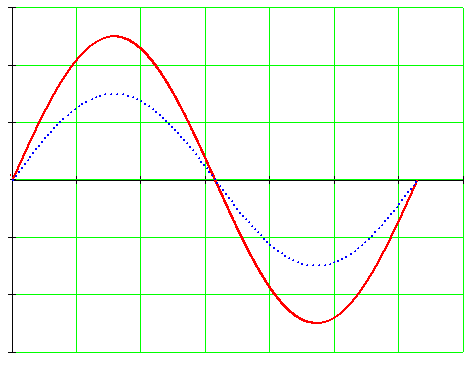
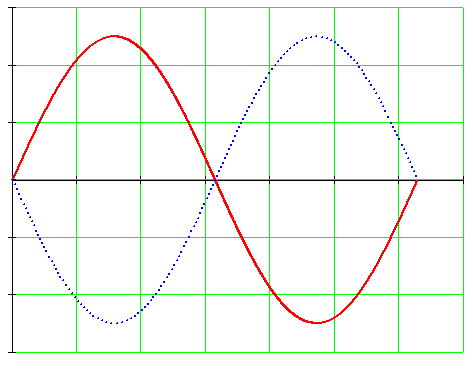
Рис. 10.5

Если две синусоиды одинаковой частоты достигают одновре­менно своих нулевых и амплитудных значений разных знаков (рис. 10.56), то они находятся в противофазе.

Среднее значение переменного тока равно величине такого постоянного тока, при котором через поперечное сечение проводника проходит то же количество электричества, что и при пере­менном токе.

Таким образом, среднее значение переменного тока эквивалент­но постоянному току по количеству электричества Q, проходящему через поперечное сечение проводника в определенный проме­жуток времени.

Средние значения переменных величин обозначаются пропис­ными буквами с индексом «с», т. е. I_C, U_C, Е_C.

Если ток изменяется по синусоидальному закону, то за полови­ну периода через поперечное сечение проводника проходит опре­деленное количество электричества Q в определенном направле­нии, а за вторую половину периода через то же сечение проходит то же количество электричества в обратном направлении. Таким образом, среднее значение синусоидального тока за период равно нулю, т. е. I_C = 0.

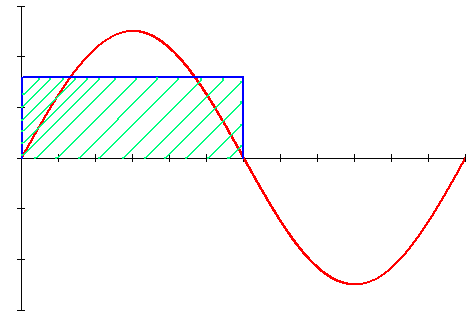
Рис. 10.6

Поэтому для синусоидального переменного тока определяется его среднее значение за половину периода Т/2, т. е.

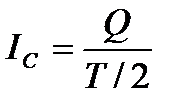
Значение переменного тока определяется выражением 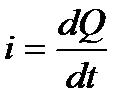, откуда 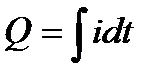. Следовательно, среднее значение синусоидального тока 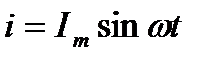с начальной фазой ψ = 0 за полупериод определяется (рис. 10.6) выражением

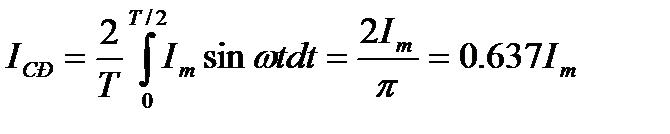
Где 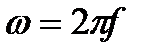, а 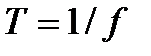. Графически среднее за полупериод значение синусоидального тока равно высоте прямоугольника с основанием, равным Т/2, и площадью, равной площа­ди, ограниченной кривой тока и осью абсцисс за по­ловину периода (рис. 10.6). Под средним значением переменной величины по­нимают постоянную со­ставляющую этой величи­ны.

Средние значения сину­соидального напряжения и ЭДС за полупериод можно определить по аналогии с током.

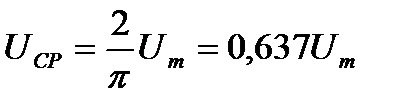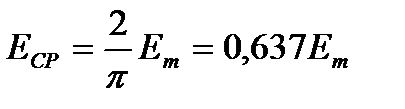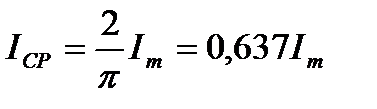; ; (10.8)

Действующее (или эффективное) значение переменного тока - это значение переменного тока, эквивалентное постоянному току по тепловому действию.

Действующее значения переменных величин обозначается про­писными буквами без индексов: I, U, E.

Действующее значение переменного тока I равно величине такого постоянного тока, которое за время, равное одному периоду пере­менного тока Т, выделит в том же сопротивлении R такое же ко­личество тепла, что и переменный ток I:

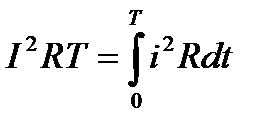
Откуда действующее значение переменного тока

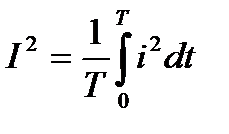или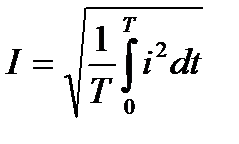

Если переменный ток изменяется по синусоидальному закону с начальной фазой, равной нулю, т.е. 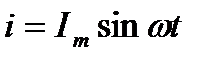, то действующее значение такого синусоидального тока будет равно

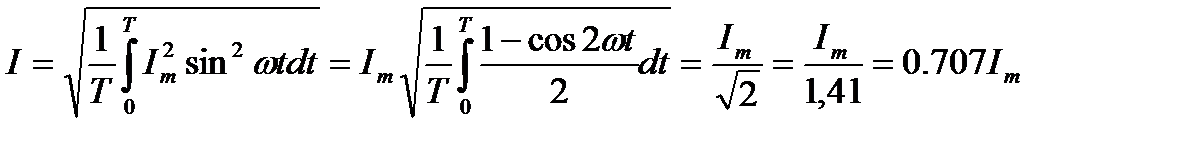
так как 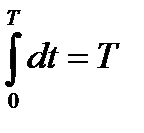, а

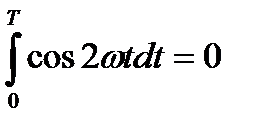
Действующее значение синусоидального тока в 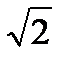=1,41 раза ме­ньше его амплитудного значения. Так же можно определить действующие значения синусоидального напряжения и ЭДС.

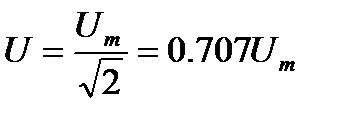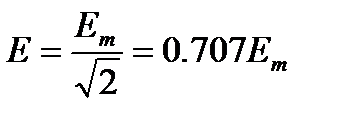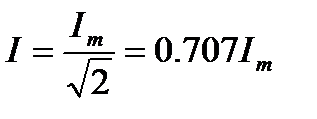; ; (10.9)

Номинальные значения тока и напряжения в электрических цепях и устройствах выражаются их действующими значениями. Так, например, стандартные напряжения электрических сетей U = 127 В или U = 220 В выражают действующие значения этих на­пряжений. А изоляцию необходимо рассчитывать на амплитудное значение этих напряжений, т. е.

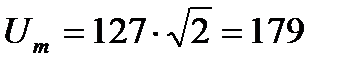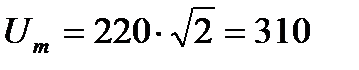В или В.

При расчете цепей переменного тока и их исследованиях чаще всего пользуются действующими (эффективными) значениями тока, напряжения и ЭДС.

На шкалах измерительных приборов переменного тока указыва­ется действующие значение переменного тока или напряжения.

Именно действующие значения тока, напряжения и ЭДС ука­зываются в технической документации, если нет специальных оговорок.

ЗАКОН ОМА В КОМПЛЕКСНОЙ ФОРМЕ ДЛЯ РЕЗИСТИВНОГО, ИНДУКТИВНОГО И ЕМКОСТНОГО ЭЛЕМЕНТОВ

Зависимости между токами и напряжениями резистивных, индуктивных и емкостных элементов определяется происходящими в них физическими процессами. Рассмотрим их по отдельности на примере закона Ома для этих элементов.

Резистивный элемент. Выберем положительное направление синусоидального тока

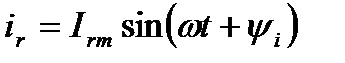(1)

в резистивном элементе с постоянным сопротивлением r совпадающим с положительным направлением синусоидального напряжения, приложенному к элементу. В этом случае для мгновенных значений напряжения и тока справедливо соотношение, определяемое законом Ома:

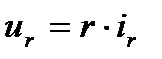(2)

или

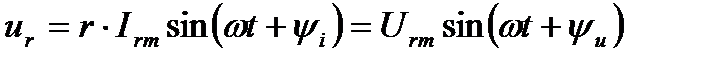(3)

где амплитуда тока и напряжения связаны соотношением:

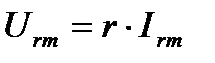(4)

а их начальные фазы одинаковы

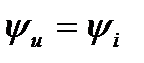(5)

т.е. ток и напряжение в резистивном элементе изменяются синфазно – совпадают по фазе, как показано на рис. 1 для начальной фазы .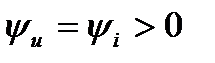

Разделив правую и левую часть выражения (4) на 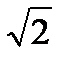, получим соотношение для действующих значений напряжения и тока резистивного элемента:

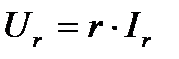(6)

Представим теперь синусоидальные напряжения и ток резистивного элемента соответствующими комплексными значениями:

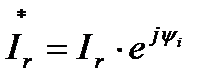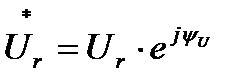и (7)

Так как 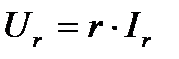и 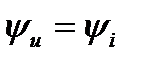, то для комплексных значений тока и напряжения резистивного элемента получим закон Ома в комплексной форме:

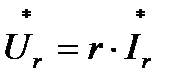(8)

Соотношение между комплексными значениями тока и напряжения для резистивного элемента наглядно иллюстрируется векторной диаграммой элемента (рис. 2). Из векторной диаграммы также видно, что векторы комплексных значений тока и напряжения резистивного элемента совпадают по фазе.

Рис.

Рис.

Индуктивный элемент. Если в индуктивном элементе ток синусоидальный

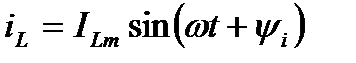(9)

то по закону электромагнитной индукции на индуктивном элементе появится напряжение:

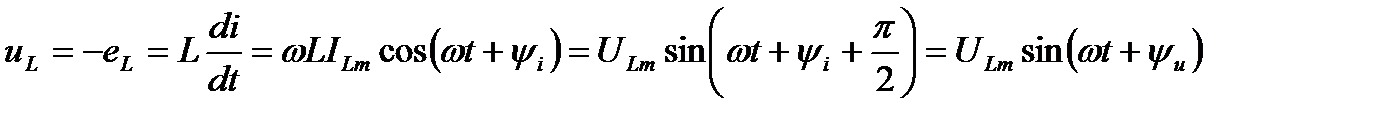(10)

где амплитуды напряжения и тока связаны соотношением:

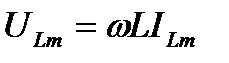(11)

а их начальные фазы – соотношением

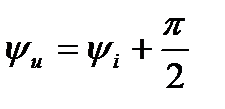(12)

Разделив правую и левую часть выражения (11) на 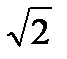, получим соотношение для действующих значений напряжения и тока индуктивного элемента:

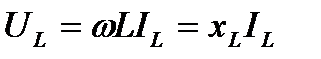(13)

На рис. 3 показан график мгновенных значений синусоидального тока и напряжения индуктивного элемента (построен при 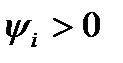) из которого видно, что синусоидальный ток отстает по фазе от синусоидального напряжения на угол .

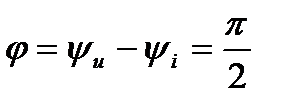Величина 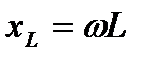в выражении единица которой Ом, называется индуктивным сопротивлением, а обратная величина 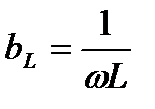– индуктивной проводимостью. Значение величин x_L и b_L являются параметрами индуктивных элементов цепей синусоидального тока.

Индуктивное сопротивление пропорционально угловой частоте синусоидального тока, при постоянном тока оно равно нулю. По этой причине многие аппараты и машины, предназначенные для работы в цепях переменного тока, нельзя включать в цепь постоянного тока.

Представим синусоидальный ток и напряжение индуктивного элемента соответствующими комплексными значениями:

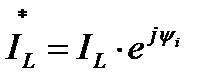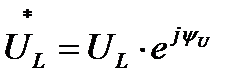и (14)

На рис. 4 приведена векторная диаграмма для индуктивного элемента. На векторной диаграмме показано, что вектор комплексного значения тока отстает по фазе от вектора комплексного значения напряжения на угол 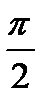, что соответствует сдвигу фаз на рис. 3. Закон Ома в комплексной форме для индуктивного элемента:

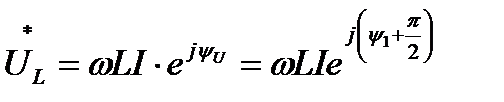(15)

Или

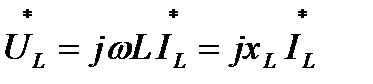(16)

Входящие в это выражения величины 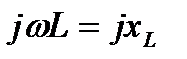называются комплексными сопротивлениями индуктивного элемента, а обратная ей величина 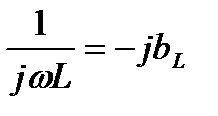– комплексной проводимостью индуктивного элемента.

Комплексное значение напряжения на индуктивном элементе можно выразить и через комплексное значение потока сцепления:

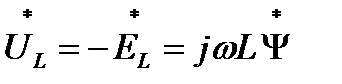(17)

Это - математическая формулировка закона электромагнитной индукции в комплексной форме.

Емкостной элемент. Если напряжение между выводами емкостного элемента изменяется по синусоидальному закону:

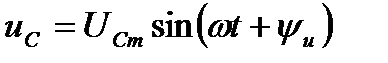(18)

то синусоидальный ток

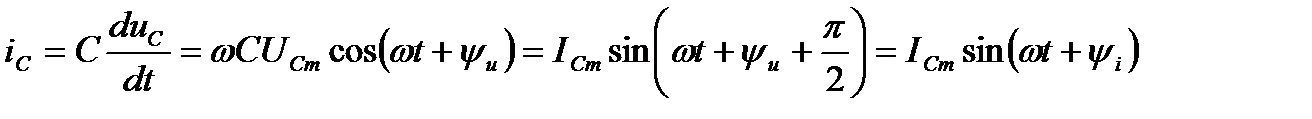(19)

где амплитуды связаны соотношением

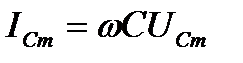(20)

а начальные фазы соотношением

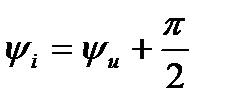(21)

Разделив правую и левую часть выражения (20) на 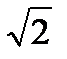, получим соотношение для действующих значений напряжения и тока емкостного элемента:

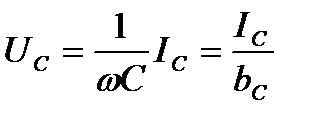(22)

Величина 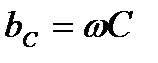в выражении (22) единица которой Ом^-1 = См, называется емкостной проводимостью, а обратная величина 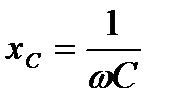– емкостным сопротивлением. Значение величин x_C и b_C являются параметрами емкостного элемента цепей синусоидального тока.

В противоположность индуктивному сопротивлению емкостное сопротивление уменьшается с увеличением частоты синусоидального тока. При постоянном напряжении емкостное сопротивление бесконечно велико.

На рис 5 показан график мгновенных значений синусоидальных напряжений и тока для емкостного элемента (построен при 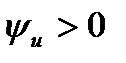) из которого видно, что синусоидальные напряжение отстает по фазе от синусоидально тока на угол 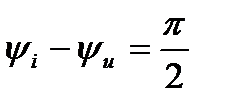, т.е. сдвиг по фазе между напряжением и током .

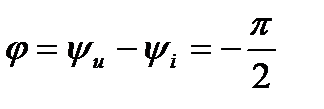Представим синусоидальный ток и напряжение емкостного элемента соответствующими комплексными значениями:

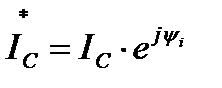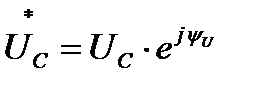и (23)

На рис. 6 приведена векторная диаграмма для емкостного элемента. На векторной диаграмме показано, что вектор комплексного значения напряжения отстает по фазе от вектора комплексного значения тока на угол .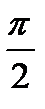

Закон Ома в комплексной форме для емкостного элемента:

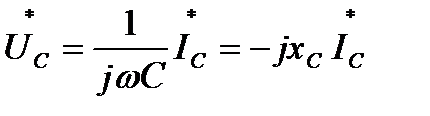(24)

Величина 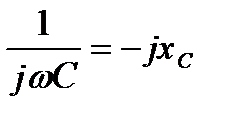, входящая в это выражение, называется комплексным сопротивлением емкостного элемента, а обратная ей величина 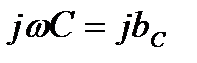– комплексной проводимостью емкостного элемента.

Рис.