В геодезии за ось абсцисс принимается направление среднего осевого меридиана зоны, а за ось ординат – направление экватора.
Предмет и задачи геодезии
Геодезия – наука об измерениях на земной поверхности, проводимых с целью определения формы и размеров Земли, составления планов и карт, а также решения различных инженерных задач на местности.
Определение формы и размеров Земли входит в задачи высшей геодезии. Вопросы, связанные с составлением планов и карт и с решением инженерных задач, относятся к геодезии.
Геодезические работы делятся на полевые и камеральные.
Полевые работы состоят из измерений горизонтальных и вертикальных углов, а также горизонтальных, вертикальных и наклонных расстояний. Камеральные работы состоят из вычислений результатов полевых измерений и графических построений.
Геодезия тесно связана с рядом других наук – математикой, физикой, астрономией, географией, геологией, геоморфологией и др.
Инженерная геодезия - решает задачи, связанные:
· с построением опорной геодезической основы для проведения съёмочных и разбивочных работ;
· составлением крупномасштабных планов и профилей для проектирования инженерных сооружений;
· производством разбивочных работ в плане и по высоте при строительстве зданий и сооружений;
· обслуживанием строительно-монтажных операций;
· составлением исполнительных чертежей объектов;
· наблюдениями за деформациями в процессе строительства.
Основные сведения о форме и размерах Земли
Предметом изучения геодезии являются геометрические свойства поверхности Земли.
Физическая поверхность Земли состоит из суши и водной поверхности и имеет сложную форму.
Обобщённое представление о форме Земли можно получить, воспользовавшись понятием «уровенная поверхность».
Уровенной поверхностью называется замкнутая поверхность, огибающая Землю, нормальная к отвесным линиям в любой своей точке.
В геодезии особое значение имеет уровенная поверхность, совпадающая со средним уровнем океанов, находящихся в состоянии покоя. Такая замкнутая поверхность, продолженная под материками перпендикулярно к направлению отвесной линии в каждой точке, называется основной уровенной поверхностью.
Тело, ограниченное основной уровенной поверхностью, называют геоидом.
Геоид не совпадает ни с одной математической фигурой и представляет собой неправильную форму.
Математическая форма Земли соответствует поверхности эллипсоида, который называется референц – эллипсоид Красовского.
Системы координат
Положение точек на земной поверхности определяется в различных системах координат:
· Система географических координат – за начало отсчёта принимается Гринвичский меридиан и плоскость экватора.
· Система геодезических координат определяет положение точек на поверхности эллипсоида вращения.
· Зональная система прямоугольных координат Гаусса (рис.1).
Чтобы установить связь между географическими и прямоугольными координатами, применяют способ проектирования поверхности земного шара на плоскость по частям, которые называют зонами (рис.1). счёт зон ведётся на восток от Гринвичского меридиана.
Прежде чем спроектировать такую зону на плоскость, её проектируют на поверхность цилиндра. После чего цилиндр развёртывают на плоскости и получают на ней изображение проекции данной зоны. Такая проекция называется проекцией Гаусса – Крюгера.
В такой системе начало координат для всех зон принимается в точке пересечения осевого меридиана данной зоны с экватором. Координатными осями являются ось абсцисс – Х и ось ординат – У (рис.2).
Рис. 1 Деление на зоны
Абсциссы, отсчитываемые от экватора к северному полюсу, считаются положительными, к южному – отрицательными. Значения ординат от осевого меридиана на восток – положительные, на запад – отрицательные.
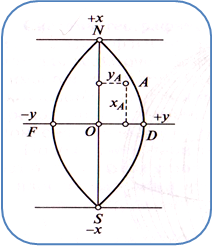
Рис.2. Зональная система координат
· Система прямоугольных координат (рис.3).
В геодезии за ось абсцисс принимается направление среднего осевого меридиана зоны, а за ось ординат – направление экватора.
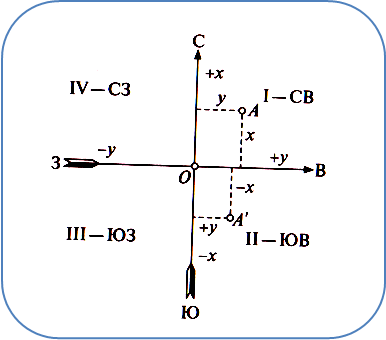
Рис. 3 Система прямоугольных координат
Оси координат делят плоскость чертежа на четыре части, которые называются координатными четвертями: I – CВ, II – ЮВ, III – ЮЗ, IV – СЗ (рис.3).
· Полярная система координат.
Положение любой точки на плоскости определяется радиус-вектором – r и углом – β, отсчитываемым по ходу часовой стрелки от линии – ОХ (полярной оси) до радиуса -вектора (рис.4).
Х А
β
r
О
рис.4 Полярная система координат
Высоты точек
Высоты точек могут быть абсолютными и условными. Если высота точки определена от уровенной поверхности, то она считается абсолютной. От любой другой поверхности – условной.
Превышение (h) – разница между высотами точек.
hА = НА – НВ
Числовые значения высот точек называются отметками.
В России высоты точек отсчитываются от уровня Балтийского моря.
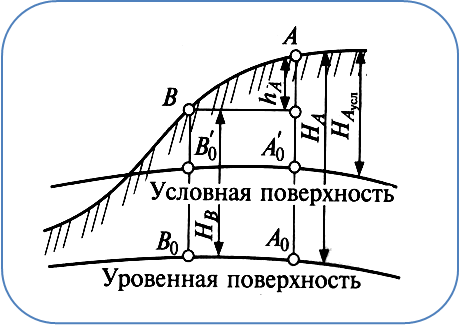
Рис. 5 Абсолютные и условные отметки.
Дата добавления: 2016-09-26; просмотров: 9588;
Поиск по сайту
Узнать еще
- II закон Ньютона в векторной и координатной форме
- А) Система астрономических координат
- Абсолютные и относительные координаты
- Автоматизация как направление дальнейшего совершенствования управления силами и средствами
- Алгоритм построения главного меридиана однополостного гиперболоида,
- Атипичное течение острого среднего отита.
- Аффинные (косоугольные) координатные системы.
- б). Система геодезических координат
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
Публикации по медицине
