Свободной и несвободной МТ
Используя основной закон динамики и формулы для ускорения МТ при различных способах задания движения, можно получить дифференциальные уравнения движения как свободной, так и несвободной МТ с той лишь разницей, что для несвободной МТ ко всем приложенным к МТ активным (заданным) силам надо добавить на основании аксиомы связей – принципа освобождаемости (Ч. 2 Статика) силы пассивные (реакции связи), а в некоторых случаях и уравнения наложенных на МТ связей.
Так как система сил, приложенных к МТ, является сходящейся, то она всегда может быть приведена к равнодействующей.
Пусть 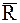 – равнодействующая системы сходящихся сил, действующих на МТ.
– равнодействующая системы сходящихся сил, действующих на МТ.
Для свободной МТ равнодействующая равна геометрической сумме сходящихся активных сил, действующих на нее:
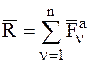 ,
,
где 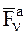 – n-я активная (заданная) сила, действующая на МТ, n – количество активных сил.
– n-я активная (заданная) сила, действующая на МТ, n – количество активных сил.
Для несвободной МТ равнодействующая равна геометрической сумме сходящихся активных (заданных) сил и пассивных сил (сил реакций связей):
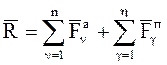 ,
,
где 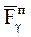 – g-я пассивная сила (сила реакции связи), действующая на МТ, h - количество пассивных сил.
– g-я пассивная сила (сила реакции связи), действующая на МТ, h - количество пассивных сил.
На основании второго закона динамики (1.2) с учетом соотношения (1.3) (Ч. 1 Кинематика), определяющим формулу для ускорения МТ при векторном способе задания движения:
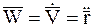 ,
,
получим дифференциальное уравнение движения МТ постоянной массы в векторной форме (рис. 1):
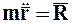 . (1.6)
. (1.6)
Спроектировав соотношение (1.6) на оси декартовой системы координат Oxyz и использовав соотношения (1.12) (Ч. 1 Кинематика), определяющее проекцию ускорения МТ на оси декартовой системы координат:
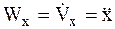 ,
, 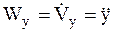 ,
, 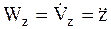 ,
,
получим дифференциальные уравнения движения МТ в проекциях на эти оси (рис. 1):
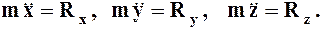 (1.7)
(1.7)
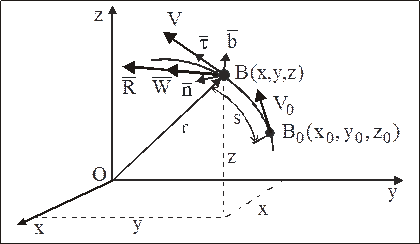
Рис.1
Спроектировав соотношение (1.2) на оси естественного трехгранника ( 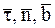 ) и использовав соотношения (1.26) и (1.28) (Ч. 1 Кинематика), определяющие формулы для ускорения МТ
) и использовав соотношения (1.26) и (1.28) (Ч. 1 Кинематика), определяющие формулы для ускорения МТ
при естественном способе задания движения:
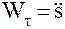 ,
, 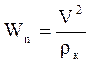 ,
, 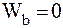 ,
,
получим дифференциальные уравнения движения МТ в проекциях на оси естественного трехгранника (рис. 1):
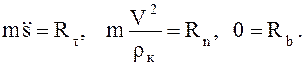 (1.8)
(1.8)
Рассмотрены наиболее используемые случаи уравнений движения МТ. Аналогично можно получить дифференциальные уравнения движения МТ в других системах координат (полярной, цилиндрической, сферической и т. д.).
Дата добавления: 2016-06-05; просмотров: 1677;











