Методы «свободной геометрии»

Действующие нормативные документы допускают, проектирование продольного профиля в классе ломаных линий (см. разд. 29.3). Проектная линия в классе ломаных представляет собой дискретный аналог гибкой кривой переменного радиуса. Ограничения по кривизне в этом случае косвенно обеспечиваются ограничениями на алгебраическую разность уклонов двух смежных отрезков прямых. Необходимость проектирования проектной линии в классе ломаных возникает чаще всего при ремонте и реконструкции автомобильных дорог, когда математическая модель проектной линии в виде последовательности прямых и дуг окружностей (квадратных парабол) оказывается недостаточно гибкой для получения приемлемого проектного решения. Особенно очевидным это становится при проектировании микропрофилирования ремонтируемых покрытий.

При автоматизированном проектировании описание проектной линии в классе ломаных требует определенной математической формализации. Наиболее просто и эффективно эта задача формализуется в терминах и математических построениях сплайн-функций, а ломаная линия собственно и является линейным сплайном или сплайном 1-й степени.

Сплайны 1-й степени (ломаные) достаточно просты для понимания и, в то же время, отражают основные свойства сплайн-функций. С математической точки зрения, сплайн 1-й степени - это кусочно-непрерывная функция, на каждом отрезке описываемая уравнением вида:

у = а_i + b_ix, где (29.7)

i - номер рассматриваемого интервала между узлами интерполяции х_i и x_i+1.

Как следует из уравнения (29.7), на элементарном интервале вид уравнения не отличается от общепринятого выражения прямой линии. В целом, уравнение ломаной (сплайна 1-й степени) в матричной форме можно записать как:

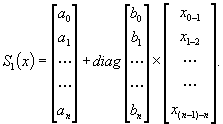(29.8)

Система линейных уравнений (29.8) не требует совместного решения и распадается на решения каждого уравнения в отдельности. Сплайн, решение которого связано с вычислением подсистем небольшой размерности (в данном случае - уравнений первого порядка) является локальным.

Интерполяционный сплайн 1-й степени - это ломаная, проходящая через точки (х_i, у_i). Для совокупности х_i (I = 0, 1,..., п) в интервале [а, b] при этом должно выполняться условие х_i < х_i+1. Используя интерполяционный полином Лагранжа можно построить сплайн для интервала i - (i+1):

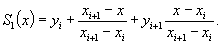
Обозначение S₁(x) понимается как сплайн-функция 1-й степени. Форму записи этой функции можно преобразовать к виду:

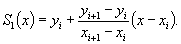
Для построения алгоритма и составления процедуры вычисления линейных сплайн-функций необходимо помнить всего лишь 2п+2 числа.

На основе интерполяционных сплайнов 1-й степени можно разрабатывать автоматизированные процедуры построения оптимальной проектной линии (см. разд. 26.3) и эвристической проектной линии, получаемой в диалоговом режиме, когда в основе проектного решения лежат интуиция и опыт инженера-проектировщика. Суть проектирования здесь состоит в том, что эскизно намечают ломаную проектную линию и посредством «ручного» перемещения узлов излома этой линии находят приемлемое ее положение с позиции проектировщика.

Другую перспективу открывают сглаживающие линейные сплайны, на основе которых можно строить алгоритмы нахождения оптимального положения ломаной проектной линии.

В случае применения сплайнов 1-й степени функционал цели имеет вид:

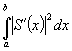
После подстановки первой производной сплайна, совпадающей в данном случае с разделенной разностью, функционал примет вид:

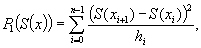где (29.9)

h_i = х_i+1 - х_i

Продифференцируем выражение (29.9) по переменной S(х_i) и сложим два последовательных слагаемых уравнения, содержащих эту неизвестную:

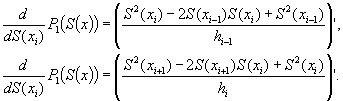
Приравняв полученную сумму нулю и выразив неизвестное S(х_i), получим рекуррентную формулу:

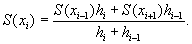
Здесь знак «=» представляет собой оператор присваивания. Если принять шаг интерполяции равномерным, то есть h_i = const, то процесс оптимизации (пошаговых итераций) в графической интерпретации будет вполне понятен (рис. 29.3).

Быстрая сходимость итерационного процесса позволяет рекомендовать этот метод для предварительной выработки проектных решений по проектной линии продольного профиля. В этом случае радиусы кривизны и уклоны проектной линии можно контролировать в системе ограничений посредством построения первых и вторых разделенных разностей.

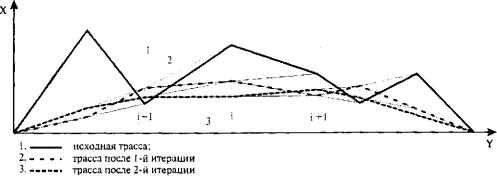
Рис. 29.3. Графическая интерпретация сглаживания линейного сплайна

Следует отметить, что методы «проекции градиента» и «граничных итераций», изложенные в разделах 29.2, 29.3, также реализованы посредством математической модели проектной линии в виде линейных сплайнов.

Более совершенные проектные решения по продольному профилю можно получить, если реализовывать проектную линию в виде функций (сплайнов) более высоких степеней, чем первая. Например, сплайны 3-й степени обладают свойством нелинейного изменения кривизны. Это свойство придает им высокую гибкость изменения формы, что чрезвычайно важно при выработке проектных решений в узкой полосе варьирования (в проектах ремонта и реконструкции автомобильных дорог). К тому же 1-я и 2-я производные этих сплайнов непрерывны, что обеспечивает контроль за величинами радиусов кривизны вертикальных кривых и законами изменения кривизны по длине трассы и в конечном итоге высокую гладкость и плавность проектной линии.

Методы проектирования продольного профиля, основанные на применении сплайнов 3-й степени (кубических), используют для описания проектной линии как интерполяционные, так и сглаживающие сплайны.

Сглаживающие сплайны необходимы для поиска оптимального положения проектной линии в заданной полосе варьирования. А интерполяционные сплайны позволяют обеспечить процесс корректировки проектной линии в интерактивном режиме работы инженера-проектировщика при эвристическом проектировании.

Для описания проектной линии на каждом интервале в виде интерполяционного кубического сплайна применяют или естественный сплайн вида:

Z_s = Z_i + B_i (S - S_i) + C_i (S - S_i)² + D_i (S - S_i)³, S_i £ S £ S_i+1.

или рациональный сплайн вила:

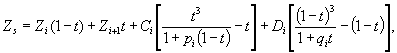где

t = (S - S_i)/h_i, h_i = S_i+1 - S_i, p_i, q_i - заданные числа, -1 < p_i, q_i < ¥.

Рациональный сплайн обладает свойствами изменения формы на любом интервале за счет варьирования величинами коэффициентов p_i, q_i, что дает возможность гибкого и точного приближения проектной линии к форме рельефа или существующим очертаниям реконструируемой (ремонтируемой) автомобильной дороги.

Сглаживающие кубические сплайны, применяемые для оптимизации положения проектной линии, как правило, минимизируют функционал вида:

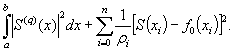
Вычисление сглаживающих сплайнов 3-й степени осуществляют методами «покоординатного спуска» или «штрафных функций».

Современные системы автоматизированного проектирования автомобильных дорог содержат, как правило, алгоритмы построения проектных линий продольного профиля как на основе традиционного математического аппарата (прямые, круговые кривые, квадратные параболы), так и на основе сплайн-функций.