Модуль деформаций бетона
Начальный модуль упругости бетона при сжатии ( 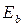 )соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях
)соответствует лишь упругим деформациям, возникающим при мгновенном загружении или при напряжениях 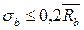 . Он определяется, в соответствии с законом Гука, как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 16), т.е.:
. Он определяется, в соответствии с законом Гука, как тангенс угла наклона прямой упругих деформаций к оси абсцисс (рис. 16), т.е.:
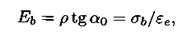 (1.18)
(1.18)
где ρ = 1 МПа – масштабно-размерный коэффициет.
Обычно 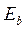 определяется из специальных опытов на призмах при низком уровне напряжений (
определяется из специальных опытов на призмах при низком уровне напряжений ( 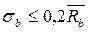 ), когда бетон можно рассматривать как упругий материал, или, если известна кубиковая прочность бетона, то по различным эмпирическим формулам. Так для тяжёлого бетона естественного твердения
), когда бетон можно рассматривать как упругий материал, или, если известна кубиковая прочность бетона, то по различным эмпирическим формулам. Так для тяжёлого бетона естественного твердения
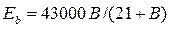 . (1.19)
. (1.19)
Значение 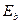 при тепловой обработке бетона снижается на 10%, при автоклавной – на 25%.
при тепловой обработке бетона снижается на 10%, при автоклавной – на 25%.
При действии на бетон нагрузки, при которой 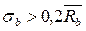 , хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бетона
, хотя бы в течение нескольких минут, в связи с развитием пластических деформаций (включая ползучесть) модуль полных деформаций бетона 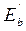 становится величиной переменной.
становится величиной переменной.
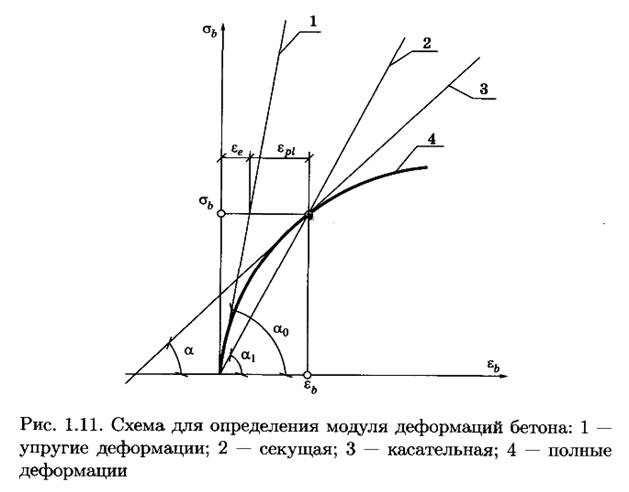
Для расчёта железобетонных конструкций пользуются средним модулем деформаций или модулем упругопластичности бетона, представляющим собой тангенс угла наклона секущей, проведённой через начало координат и точку на кривой 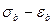 сзаданным напряжением, к оси абсцисс, т.е.
сзаданным напряжением, к оси абсцисс, т.е.
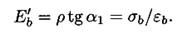 (1.20)
(1.20)
Зависимость между  и
и 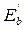 можно установить, если выразить по (1.18) и (1.20) одно и то же напряжение в бетоне
можно установить, если выразить по (1.18) и (1.20) одно и то же напряжение в бетоне 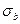 через упругие деформации
через упругие деформации 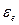 и полные деформации
и полные деформации 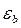
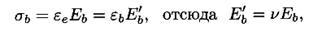 (1.21)
(1.21)
где v = 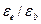 – коэффициент упругопластичности бетона. Значение v при сжатии изменяется от 1 (при упругой работе бетона) до 0,15 (в момент, предшествующий разрушению бетона при очень длительном загружении).
– коэффициент упругопластичности бетона. Значение v при сжатии изменяется от 1 (при упругой работе бетона) до 0,15 (в момент, предшествующий разрушению бетона при очень длительном загружении).
Начальный модуль упругости бетона при растяжении 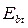 по абсолютной величине принимается равным
по абсолютной величине принимается равным 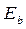 ,т.е.
,т.е. 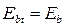 , а
, а
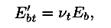 (1.22)
(1.22)
где vt = 0,15 – значение коэффициента упругопластичности бетона при растяжении в момент, предшествующий разрушению.
Значения модуля сдвига бетона G принимают по установленной в теории упругости зависимости
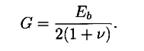
Подставив в неё начальный коэффициент поперечной деформации бетона ν = 0,2, получим 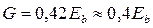 .
.
Дата добавления: 2021-09-07; просмотров: 1175;











