Гидродинамический пограничный слой

Рис. 20 Изменение скорости в гидродинамическом пограничном слое
Рассмотрим продольное обтекание плоской поверхности тела безграничным потоком жидкости. Скорость равна w0, а температура Т0.
При соприкосновении частиц жидкости с поверхностью тела они «прилипают» к ней. В результате в области около пластины вследствие действия сил вязкости образуется тонкий слой заторможенной жидкости, в пределах которого скорость изменяется от нуля на поверхности тела до скорости невозмущенного потока (вдали от тела). Этот слой заторможенной жидкости называется гидродинамическим пограничным слоем. (Теория гидродинамического пограничного слоя впервые дана в 1904 г. Л. Прандтлем).
Чем больше расстояние х от передней кромки пластины, тем толще пограничный слой, так как влияние вязкости по мере движения жидкости вдоль тела все дальше проникает в невозмущенный поток.
Для течения жидкости внутри пограничного слоя справедливо условие ¶wх/¶у ¹ 0;
вне пограничного слоя и на его внешней границе ¶wх/¶у = 0 и wх = w0.
Понятия «толщина пограничного слоя» и «внешняя граница пограничного слоя» довольно условны, так как резкого перехода от пограничного слоя к течению вне слоя нет. Скорость в пограничном слое по мере увеличения у асимптотически стремиться к w0.
Поэтому под толщиной пограничного слояd подразумевается такое расстояние от стенки, на котором скорость будет отличаться от скорости потока вдали от тела на определенную заранее заданную малую величину e << 1 (например на 1%) при у = d wх = (1 - e)w0.
Таким образом, при омывании тела поток жидкости как бы разделяется на 2 части: на пограничный слой и внешний поток. Во внешнем потоке преобладают силы инерции, вязкостные силы здесь не появляются. Напротив, в пограничном слое силы вязкости и инерции соизмеримы.
Соотношение сил инерции и сил вязкости характеризуется числом Рейнольдса:
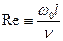 ,
,
где w0 – скорость невозмущенного потока; n - кинематическая вязкости (м2/с); l – масштаб продольной координаты.
Таким образом, теория пограничного слоя приобретает характер метода упрощения математической формулировки краевой задачи и связанной с этим возможности решения.
Дата добавления: 2021-09-07; просмотров: 651;











