Теорема о работе равнодействующей
Теорема.Работа равнодействующей системы сил на каком-то участке пути равна алгебраической сумме работ составляющих сил на том лее участке пути.
Пусть к материальной точке М приложена система сил (F1, F2, F3,…, Fn), равнодействующая которых равнаF 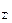 (рис. 15.3).
(рис. 15.3).
Система сил, приложенных к материальной точке, есть система сходящихся сил, следовательно,
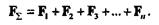
|
Спроецируем это векторное равенство на касательную к траектории, тогда
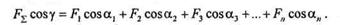
Умножим обе части равенства на бесконечно малое перемещение ds и проинтегрируем это равенство в пределах какого-то конечного перемещения s:
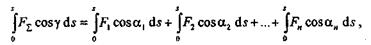
|
что дает равенство
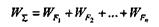
или сокращенно
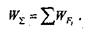
Теорема доказана.
Пример 15.1. Вычислить работу, которая производится при равномерном подъеме груза G= 200 Н по наклонной плоскости на расстояние s = 6 м, если угол, образуемый плоскостью с горизонтом,  =30°, а коэффициент трения скольжения равен f = 0,01 (рис. 15.4).
=30°, а коэффициент трения скольжения равен f = 0,01 (рис. 15.4).
Решение. Разложим силу тяжести G груза на две взаимно перпендикулярные составляющие G1 и G2— соответственно параллельную и перпендикулярную наклонной плоскости. Согласно второму закону трения скольжения, сила трения Fтр равна
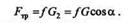
Применив теорему о работе равнодействующей, вычислим искомую работу как сумму работ сил сопротивления (работа силы G2 и нормальной реакции Nравна нулю, так как эти силы перпендикулярны направлению перемещения s):
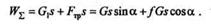
Подставив числовые значения, получим
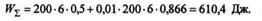
|
Дата добавления: 2021-09-07; просмотров: 624;











