Классификация механических связей
В аналитической механике необходимо более подробно рассмотреть связи, налагаемые на точки механической системы. Механической системой, как известно, называют любую совокупность материальных точек. Условия, ограничивающие свободу перемещения точек механической системы, называются связями. Математически связи могут быть выражены уравнениями или неравенствами, в которые входят время, координаты всех или части точек системы и их производные но времени различных порядков. Для одной точки уравнение связи в общем случае можно выразить в форме
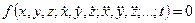 . (217)
. (217)
В дальнейшем ограничимся рассмотрением связей, в уравнения которых могут входить производные по времени от координат не выше первого порядка.
Для механической системы, состоящей из 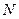 точек,
точек, 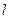 уравнений связей представятся системой уравнений
уравнений связей представятся системой уравнений
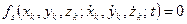 ,
, 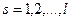 . (218)
. (218)
Считается, что индекс 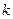 принимает все или часть значений от 1 до
принимает все или часть значений от 1 до 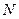 как для координат, так и для их производных.
как для координат, так и для их производных.
Если в уравнения связей (218) входят только координаты точек и не входят производные от координат, то связи называются геометрическими.
Если в уравнения связей кроме координат входят еще и их производные по времени (проекции скоростей точек на оси координат) или только одни производные, кроме времени, то связи называются кинематическими.
Все геометрические и интегрируемые кинематические связи называются голономными. Неинтегрируемые кинематические связи, которые нельзя свести к геометрическим, являются неголономными.
Связи, в уравнения которых время явно не входит, называются стационарными или склерономными. Если время входит явно в уравнение связи, то связь называется нестационарной и реономной.
Связи называют неосвобождающими или двусторонними, если они выражаются математически уравнениями, и освобождающими или односторонними, если они выражаются неравенствами.
Все связи можно разделить на реальные и идеальные. К идеальным связям относятся все связи без трения. Некоторые связи с трением тоже относятся к идеальным. Понятие идеальных связей дается после введения понятия возможного перемещения системы.
Дата добавления: 2017-09-01; просмотров: 1198;











