Основы теории подобия и анализа размерности.
Исследования процессов с целью получения уравнений, возможно проводить чисто теоретическим путем на основе общих законов физики и химии это наиболее желательный путь исследования процесса, конечным итогом которого является решение уравнений, полностью описывающих процессы.
Пример:
Для идеальных жидкостей решение дифференциального уравнения равновесия и движения Эйлера является основное уравнение гидростатики и уравнение Бернулли. Но большинство процессов химической технологии зависят от такого большого количества переменных, что удается дать лишь математическую формулировку задачи, полученные уравнения не могут быть решены известными способами.
Пример: дифференциальные уравнения Навье-Стокса.
С аналогичными трудностями приходится сталкиваться и при тепловых и при массообменных процессах, процессах в реакторе, где химические превращения осложняются движением потоков и тепло-массообменными процессами.
В таких случаях, для нахождения связей между величинами, характеризующими процесс, прибегают к экспериментальному исследованию, то есть к проведения опытов.
На основе опытов часто получаются эмпирические уравнения, которые являются частными и не могут быть распространены на условия отличные от тех, в которых они получены.
Теория подобия дает возможность так ставить опыты и обрабатывать расчеты, чтоб при проведении, небольшого числа опытов, иметь возможность обобщать результат, получая уравнения для всех подобных явлений.
Используя теорию подобия, позволяющую вместо опытов на аппаратах промышленного масштаба проверять исследования на моделях значительно меньшего размера.
Таким образом, методы теории подобия лежат в основе масштабирования и моделирования процессов.
ü Различают физическое математическое моделирование.
v При физическом моделирование процесс изучается на материальных моделях только в аппаратах меньших размеров, но физическая сущность изучаемых процессов в модели и в натуре остается одинаковой.
ЛЕКЦИЯ 8.
Подобными называются явления, для которых постоянны отношения характеризующих их сходственных величин.
Необходимые условия подобия:
· Геометрическое подобие, т.е. подобие сходственных геометрических величин.
· Временное подобие.
· Подобие полей физических величин, т.е. в сходных точках пространства физические величины подобны.
· Подобие начальных и граничных условий.
Достаточные условия:
Процессы, происходящие в модели и в натуре, должны описываться одинаковыми дифференциальными уравнениями.
Основные понятия теории подобия.
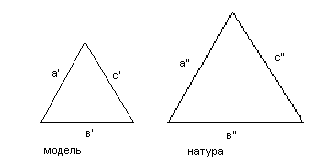
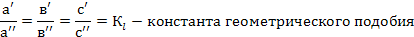
Кl изменяется при изменении масштаба.

i – представляет собой выражение величины в относительных единицах.
Инвариант, выраженный отношением двух подобных величин, называется симплексом.
Если инвариант выражен отношениями разнородных величин, но является безразмерным, то такой инвариант называется критерием подобия.
· Геометрическое подобие соблюдается при равенстве всех сходных линейных размеров

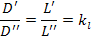
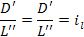
| 1 аппарат | 2 аппарат | |
| Загрузка | τ1' | τ1'' |
| Перемешивание | τ2' | τ2'' |
| Нагрев | τ3' | τ3'' |
| Выгрузка | τ4' | τ4'' |
· Временное подобие
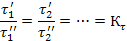
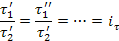
При соблюдении геометрического и временного подобия будет соблюдаться и подобие скоростей
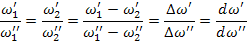
т.е. можно заменить отношение одноименных величин отношениями их приращений.
· Подобие полей физических величин.
Оно предполагает, что для двух любых сходных точек натуры и модели, размещенных подобно в пространстве и времени, отношение физических свойств является величиной постоянной.
· Подобие начальных и граничных условий предполагает, что отношение основных параметров в начале и на границе в модели и в натуре является величиной постоянной, т.е. для начальных и граничных условий, а также для других сходных точек пространства, соблюдается геометрическое, временное и физическое подобие.
Теоремы подобия.
1. Подобными являются явления, характеризующиеся численно равными критериями подобия.
| m' | m'' |
| ω' | ω'' |
| τ' | τ'' |
| G' | G'' |
Эти величины взаимодействуют по закону:
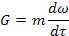
Запишем константы подобия:
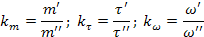
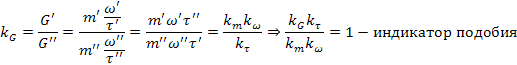
Если индикатор подобия равен 1, то явления подобны.
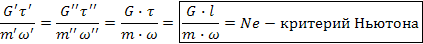
Вывод:эта теорема подобия была сформулирована Ньютоном и согласно ей, при подобии систем всегда могут быть найдены такие комплексные величины, которые для сходств точек одинаковы. Первая точка подобия, показывает, какие величины следует измерять при проведении опытов, а именно те величины, которые входят в критерии подобия.
2. Решение любого дифференциального уравнения связывающего между собой. Переменные, влияющие на процесс, могут быть предоставлены в виде зависимости между критериями подобия.
П1, П2, П3…….. П1=f(П2;П3…)
Если процесс описывает несколько критериев подобия П1, П2, П3, … такая зависимость называется критериальным уравнением; причем, П1 – определяемый критерий, П2, П3, - определяющий критерий. П1 – это такой критерий, в который входят величины, не являющиеся необходимыми для однозначной характеристики процесса. Такие критерии сами зависят от определяющих критериев, в состав которых входят условия однозначности, то есть замеряемые величины.
Для гидродинамических процессов нужно найти ∆р – эта величина будет входить в П1. Замеряемые величины (вязкость, плотность, диаметр и т.д.) – П2,П3
Вывод: Вторая теорема подобия показывает, как обрабатывать результаты опытов, проводимых на моделях. Их нужно представлять в виде функциональной зависимости между критериями подобия. (Бекингем, Афанасьева-Эленфест).
3. Кирпичев формулирует совокупность необходимых и достаточных условий подобия.
Подобны те явления, которые описываются одной и той же системой дифференциальных уравнений, и у которой численно равны определяющие критерии подобия.
Общий вывод: Исследование процесса методом теории подобия должно состоять из следующих этапов:
· Получив полное математическое описание, т.е. составив ДУ, проводят его подобное преобразование и получают критерий подобия.
· Опытным путем на моделях устанавливают конкретный вид зависимости между критериями подобия. Полученное обобщенное уравнение справедливо для всех подобных явлений в исследованных пределах измерения определяющих критериев подобия.
ЛЕКЦИЯ 9:
Дата добавления: 2017-09-01; просмотров: 3502;











