Балки рационального сечения

При заданных величинах R и 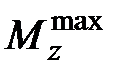из формул (10.2) определяем требуемый момент сопротивления

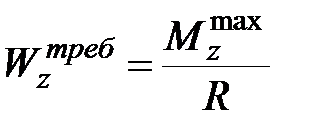
(10.5)

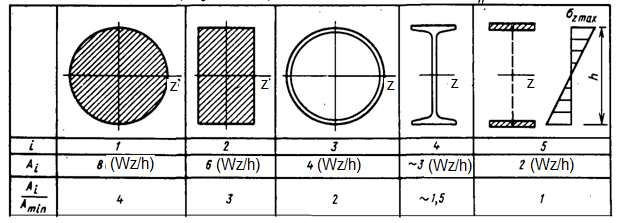
Будем считать, что значение 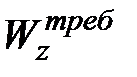задано. Для различных форм сечения одинаковой высотой h определим сечение с наименьшей площадью (балка с наименьшим расходом материала) (см. табл. 10.1).

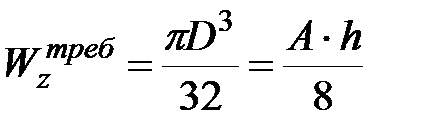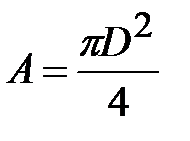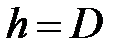Круг: (где , ), тогда .

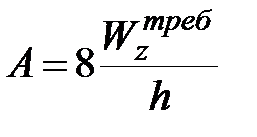Прямоугольник: 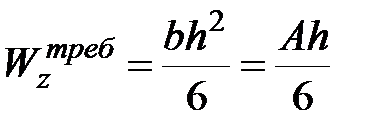, (где 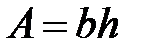, 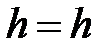), тогда .

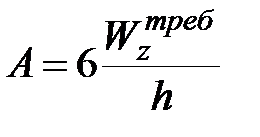Трубчатое сечение ( 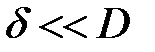) : 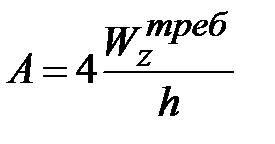. Двутавр .

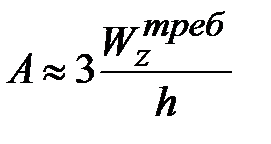Наименьшая площадь 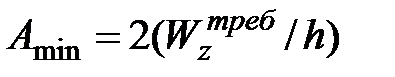требуется для идеального двутавра. У идеального двутавра площадь стенки стремиться к нулю, а вся площадь сосредоточена в полках, на уровне, где действуют максимальные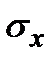

Требуемые площади при заданном значении 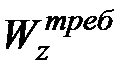представлены в табл. 10.2

Таблица 10.2

Балка со ступенчатым изменением сечения

,

.

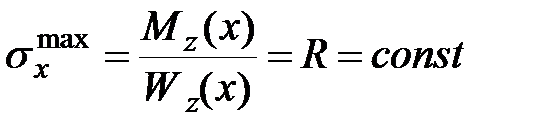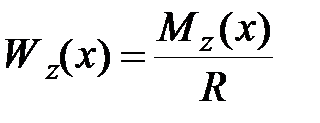(10.6)

Добиться снижения веса балки можно также путем изменения размеров сечения по ее длине в соответствии с эпюрой изгибающих моментов, увеличивая сечение там, где моменты больше, и наоборот (рис 10. 3).

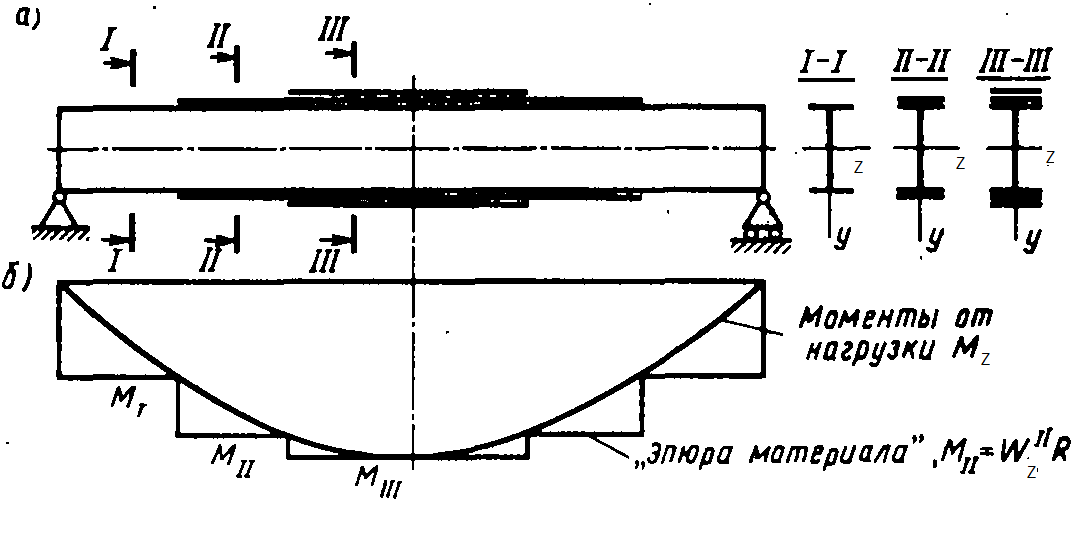
Рис. 10.3 Балка со ступенчатым изменением сечения

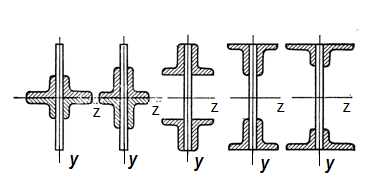
Рис 10.3,б Пять составных сечений балок с равной площадью и равной высотой ( 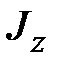, 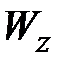- возрастают слева направо).