Движение с пересечением силовых линий.

Пусть ось х декартовой системы координат параллельна вектору напряженности электростатического поля 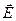, пусть вектор начального импульса 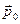материальной точки с электрическим зарядом 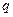лежит в плоскости z=0, аего проекция на ось у положительна. Если начальный импульс 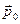не имеет составляющей вдоль оси z, если отсутствует составляющая силы в этом направлении, то, очевидно, движение материальной точки должно происходить в плоскости z=0. Уравнения динамики материальной точки можно записать в форме

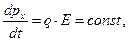
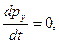
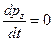. (1)

Если вектор начального импульса материальной точки составляет угол 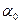с положительным направлением оси х, уравнения (1) можно проинтегрировать:

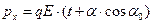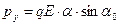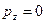, , . (2)

Здесь величина 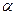имеет значение, определённое выше. Из общего соотношения (3) предыдущего раздела теперь следует:

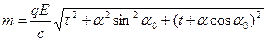. (3)

Постоянная величина 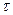также сохраняет своё определение.

Соотношения (1) и (2) позволяют рассчитать величины скоростей материальной точки вдоль осей х и у:

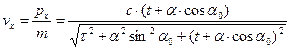, (4)

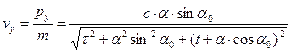. (5)

В соответствии с зависимостью (4) продольная скорость материальной точки увеличивается с течением времени и при стремлении времени движения к бесконечно большой величине приближается к скорости света в вакууме. Характер изменения продольной скорости (4) с течением времени не отличается от характера изменения скорости материальной точки в движении без пересечения силовых линий однородного электростатического поля. Поперечная скорость – зависимость (5) – монотонно уменьшается и в пределе обращается в нуль.

Ускорения материальной точки вдоль продольного и поперечного направлений получаем дифференцированием зависимостей (4) и (5):

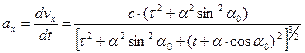, (6)

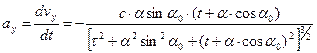. (7)

Заметим, что продольное ускорение (6) монотонно убывает с течением времени 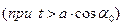, что легко объяснить возрастанием массы частицы с увеличением скорости её движения. Поперечное ускорение имеет отрицательную величину, оно стремится к нулю по абсолютной величине при стремлении времени движения частицы к бесконечно большой величине. Выражение (7) служит прекрасной иллюстрацией ограниченности понятий «здравого смысла»: сила, действующая на частицу в поперечном направлении равна нулю, импульс в поперечном направлении сохраняется, а ускорение отлично от нуля! Продольная скорость меняется не вследствие действия силы, а вследствие изменения массы частицы при изменении скорости частицы.

Зависимости (4) и (5) позволяют рассчитать изменение продольной и поперечной координат частицы с течением времени:

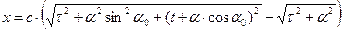, (8)

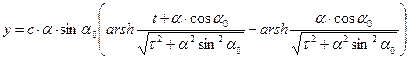. (9)

Система (8)-(9) представляет собой параметрические уравнения движения заряженной частицы в однородном электростатическом поле. Легко видеть, что движение частицы начинается из начала координат. Зависимости (8) – (9) достаточно сложны для восприятия и анализа, но если из выражения (9) найти значение 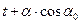и подставить его в выражение (8), т.е. исключить время из параметрических уравнений движения, то можно получить уравнение траектории движения релятивистской частицы:

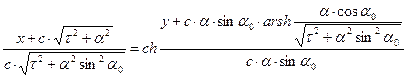. (10)

Зависимость (10) описывает так называемую «цепную линию»: 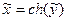, координаты х и у переходят в 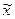и 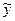с помощью преобразований смещения и сжатия.

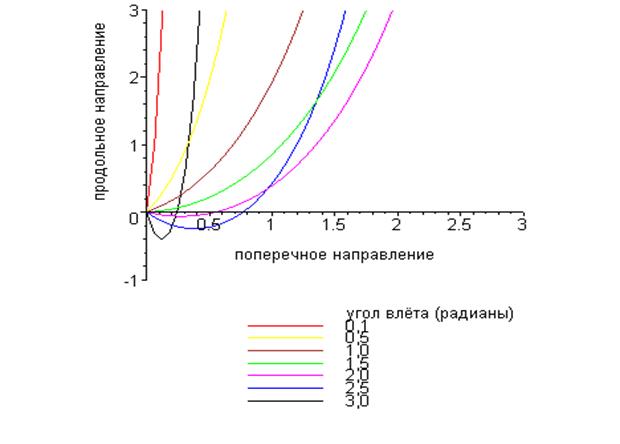
На рис. 1. показано семейство траекторий движения заряженной частицы в однородном электростатическом поле при значении параметра . Вдоль координатных осей отложены безразмерные величины 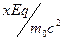и 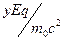. При анализе семейства траекторий движения заряженной частицы в однородном электростатическом поле следует обратить внимание на порядок расположения кривых: при малых углах 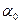и близких к величине 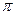(«острый влёт») траектория «прижимается» к оси x, при 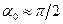(поперечный влёт) траектория заметно отклоняется от оси х. Внешне характер семейства траекторий похож на семейство траекторий движения нерелятивистской частицы. В нерелятивистском случае ( 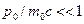, 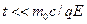) уравнение траектории (10) переходит в соотношение:

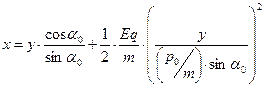. (11)

Вспомним, что траектория тела, брошенного под углом к горизонту, при рассматриваемой ориентации координатных осей имеет вид:

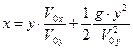. (12)

Здесь g=const - ускорение силы тяжести, V_ox и V_oy – проекции на соответствующие оси координат вектора начальной скорости тела. Совместное рассмотрение зависимостей (10), (11) и (12) позволяет выявить степень подобия и различия сравниваемых физических процессов.

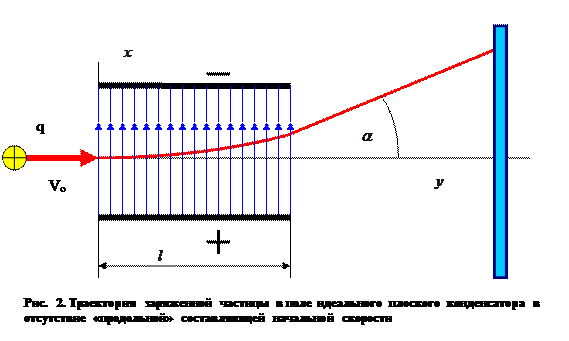
Классическое приближение (нерелятивистский случай) – соотношение (11), в частности, – лежит в основе объяснения принципа действия и расчёта управляющего воздействия электростатического поля на траекторию заряженной частицы. Так, если частица с зарядом 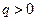и начальной скоростью V_o влетает в пространство между пластинами идеального плоского конденсатора (рис.2) без «продольной» начальной скорости, то угол отклонения траектории от первоначального направления составит величину:

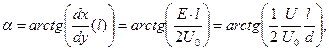(13)

где U_o - ускоряющее напряжение, обеспечивающее необходимое значение начальной скорости заряженной частицы, 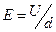- напряжённость поля, U - напряжение, d - расстояние между пластинами конденсатора, l – протяжённость конденсатора.