Проецирование точки на две плоскости проекций

Аппарат проецирования состоит из:

1) 2-х взаимно перпендикулярных плоскостей проекций П₁^ П₂;

2) 2-х направлений проецирования 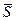₁^ П₁ и 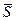₂^ П₂ .

Изобразим модель проецирования (рис.1.3).

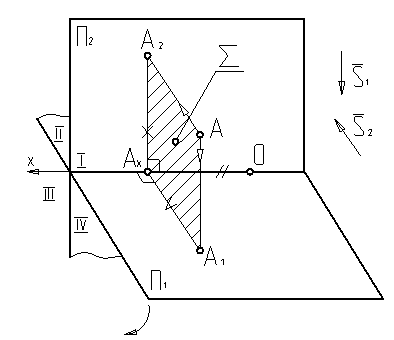
Рисунок 1.3. Модель проецирования

Две взаимно перпендикулярные плоскости делят пространство на 4 части – I, II, III, IV четверти. В данном курсе объекты исследования будут чаще всего располагаться в I четверти.

Основные понятия:

П₁ – горизонтальная плоскость проекций;

П₂ – фронтальная плоскость проекций;

х – ось проекций х, которая является линией пересечения двух плоскостей проекций x=П₁ÇП₂;

А₁ – горизонтальная проекция точки А (точки пересечения проецирующего луча, проведенного через точку А с плоскостью проекций П₁);

А₂ – фронтальная проекция точки А.

АА₁^ П₁ ® å^ П₁

АА₂^ П₂ ® å^ П₂

Таким образом плоскость å является перпендикулярной оси проекций х. Тогда А_хА₁^х и А_хА₂^х

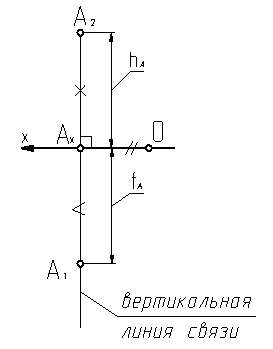
Рисунок 1.4. Комплексный чертеж точки А.

Перейдём к комплексному чертежу, совмещая П₁ вращением вокруг оси х с плоскостью проекций П₂.

При этом на комплексном чертеже остаются только проекции точки, а сама точка исчезает (рис.1.4). В пространстве - точка, на комплексном чертеже - проекции точки.

Основные понятия:

h_А – высота точки А, которая определяет расстояние точки А до горизонтальной плоскости проекций П₁;

f_А – глубина точки А, которая определяет расстояние точки А до фронтальной плоскости проекций П₂.

Сформулируем первое из основных свойств ортогонального проецирования. Проекция точки есть точка.

(1)

Сформулируйте основные свойства комплексного чертеже точки:

1) для определения положения точки в пространстве необходимо и

достаточно две проекции точки;

2) две проекции точки лежат на одной линии связи;

3) сама линия связи всегда перпендикулярна оси проекций АА₁^Х