Модель и комплексный чертеж прямых общего положения

Первый постулат Евклида гласит: через две точки можно провести прямую и только одну.

Прямая в пространстве по отношению к плоскостям проекций может занимать произвольное или частное положение. Прямая произвольно расположенная относительно плоскостей проекций называется прямой общего положения. Изобразим прямую общего положения на модели (рис.2.1).

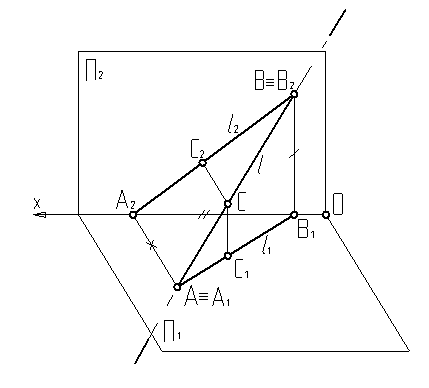
Рисунок 2.1. Модель прямой общего положения

Точку А выберем лежащей в плоскости П₁. Высота точки А равна нулю. В точке А прямая l пересекает плоскость П₁. А=l∩П₁ – горизонтальный след прямой l.

Точку В выберем лежащей в плоскости П₂. Глубина точки В равна нулю. В точке В прямая l пересекает плоскость П₂. В=l∩П₂ – фронтальный след прямой l.

Прямая l определяется двумя точками l(АВ). Перейдем к комплексному чертежу (рис.2.2).

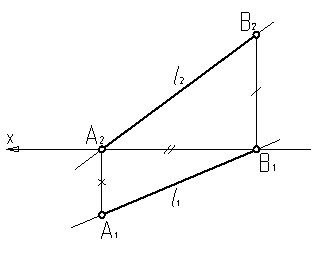
Рисунок 2.2. Комплексный чертеж прямой l

Проекции прямой общего положения на комплексном чертеже расположены под произвольными углами к осям проекций.

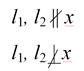
Выберем произвольную точку С на прямой l и сформируем второе свойство ортогонального проецирования.

Точка принадлежит прямой, если ее проекции принадлежат одноименным проекциям прямой.

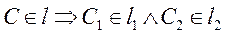
Теперь определим в каком отношении проекции точки С делят соответствующие проекции отрезка АВ.

Из ∆А₁В₁В₂ по теореме Фалеса следует:

.

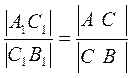Из ∆А₁А₂В₂ следует:

.

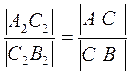Сформулируем третье правило ортогонального проецирования:

Проекция точки делит проекцию отрезка прямой в таком отношении, в каком точка делит сам отрезок.