Газ в силовом поле. Барометрическая формула. Распределение Максвелла – Больцмана. Экспериментальное определение числа Авогадро.
Хаотическое движение молекул приводит к тому, что молекулы газа равномерно распределяются по объему сосуда. Это справедливо если на молекулы не действуют внешние силы. При наличии таких сил равновесное распределение молекул нарушается.
Рассмотрим вертикальный слой воздуха с основанием dS, который находится под действием силы тяжести (рис.1).
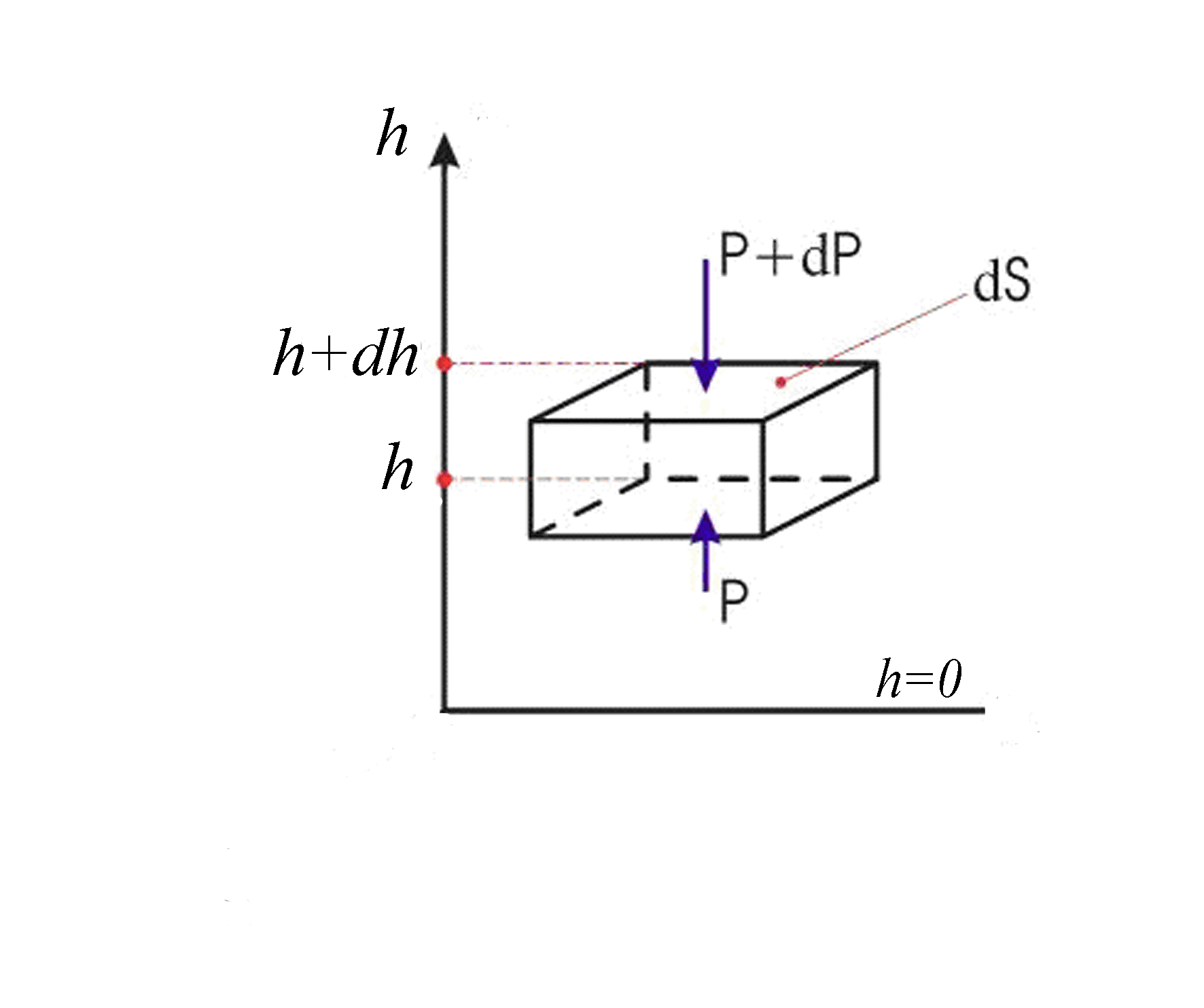
Рис.1. К выводу барометрической формулы
Пусть у поверхности земли, где h = 0, давление равно pо. Атмосферное давление p на высоте h обусловлено действием силы тяжести слоев воздуха, которые лежат выше. Давление на высоте h + dh будет равно p + dp, причем, если dh > 0, то dp < 0, так как давление с увеличением высоты уменьшается.
Разность давлений p и p + dp равна давлению газа, которое создает сила тяжести, действующая на газ, находящийся в объеме с площадью dS и высотой dh
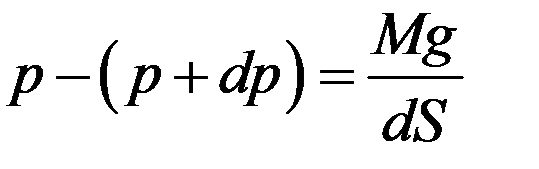 (1)
(1)
где M – масса газа, Mg – сила тяжести, действующая на газ, находящийся в рассматриваемом объеме.
Очевидно:
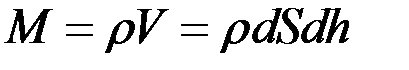 (2)
(2)
где ρ – плотность газа на высоте h, V - объем газа.
С учетом (2) из (1) получим:
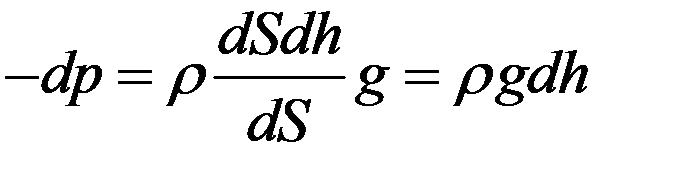 (3)
(3)
(в формуле (3) ρgdh –давление столба газа высотой dh)
Плотность газа равна произведению массы одной молекулы m на их число в единице объема, т.е. на концентрацию n:
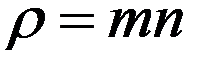 (4)
(4)
Из основного уравнения МКТ получим:
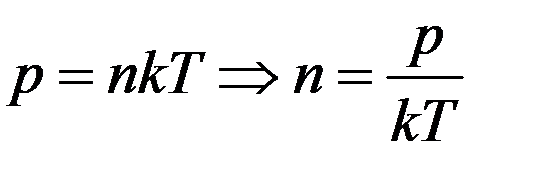 (5)
(5)
С учетом (5) из (4) получим:
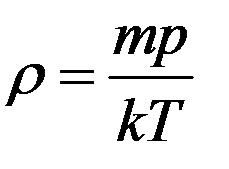 (6)
(6)
Учитывая (6) перепишем (3) в виде:
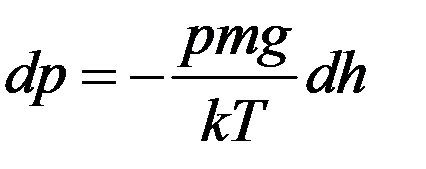 (7)
(7)
В (7) разделим переменные:
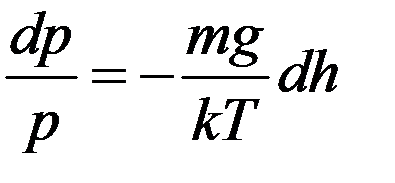 (8)
(8)
Если считать, что на всех высотах температура одинаковая T = const (что, вообще говоря, не совсем верно), то после интегрирования (8) получим:
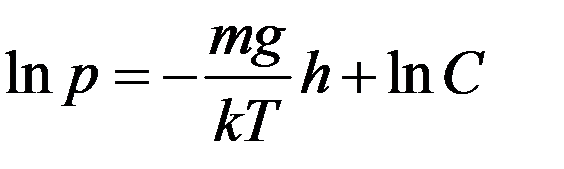 (9)
(9)
где C – постоянная интегрирования. Ее можно определить из начальных условий: если h = 0, то p = po. С учетом этого из (9) получим: C = po. Тогда:
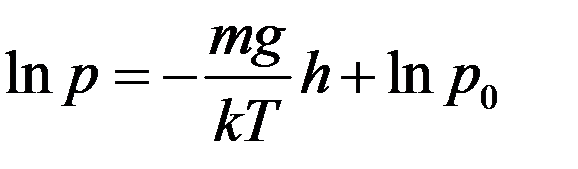
Отсюда следует, что
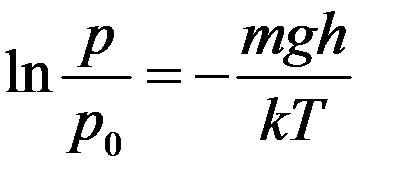
После потенцирования получим:
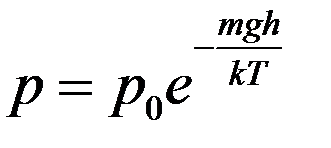 (10)
(10)
С учетом того, что
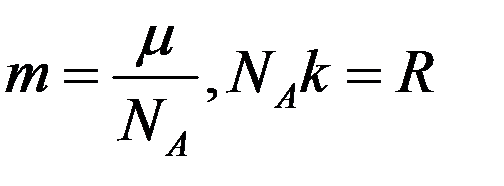
Получим:
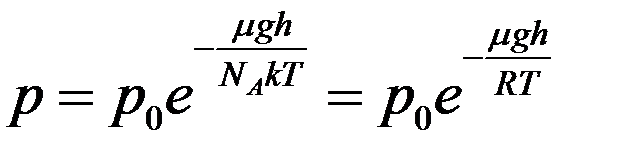 (11)
(11)
где μ – молярная масса, NA – число Авогадро, R – универсальная газовая постоянная.
Уравнения (10) и (11), выражающие закон изменения давления с высотой, называются барометрической формулой. Из этих уравнений видно, что давление уменьшается с высотой по экспоненциальному закону.
| P0 |
| h |
| P |
Pис.2. Зависимость атмосферного давления от высоты
Формулы (10) и (11) справедливы для высот 10 – 15 км, где на изменение ускорения силы тяжести с высотой можно не обращать внимания. В случае смеси нескольких газов эти формулы справедливы для парциального давления каждого газа. В соответствии с (11), чем больше молярная масса газа, тем быстрее его давление уменьшается с высотой. Следовательно, атмосфера земли должна обогащаться легкими газами с ростом высоты. Однако из-за перемешивания (ветер, конвекционные потоки) до высот 80 – 90 км атмосфера практически однородна. И только на высотах более 90 км состав атмосферы обогащен легкими газами.
С помощью барометрической формулы, зная давление p на данной высоте и давление на уровне моря po можно определить высоту над уровнем моря. Приборы, которые применяются для этих целей, представляют собой специальные барометры, шкала которых проградуирована в метрах. Они называются альтиметрами.
Известно, что:
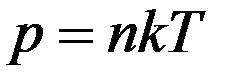
С учетом этого из (10) получим
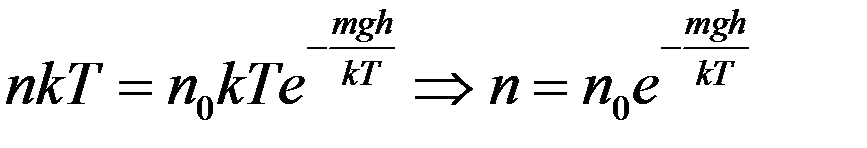 (12)
(12)
где no – концентрация молекул на высоте h = 0, n – концентрация молекул на высоте h.
Из (12) следует, что при T→∞, n→no. Это значит, что при повышении температуры газа, его молекулы стремятся равномерно распределиться по высоте. Если T→0, то и n→0. Следовательно, при абсолютном нуле температуры молекулы газа должны разместиться на поверхности земли. Из вышесказанного вытекает, что распределение молекул по высоте устанавливается в результате взаимодействия двух факторов: 1). Притяжения молекул к земле, которое характеризуется силой тяжести mg, стремится расположить их на поверхности Земли, 2). Тепловое движение молекул, которое характеризуется величиной kT, стремится распределить их равномерно по всему пространству.
В (12) mgh = Eп – потенциальная энергия молекулы на высоте h. Поэтому (12) по сути дела, является распределением молекул по значениям потенциальной энергии.
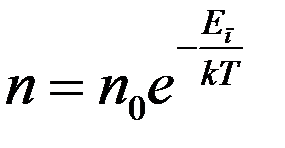 (13)
(13)
где n0 – концентрация молекул в том месте, где их потенциальная энергия равна нулю, n – концентрация молекул в том месте, где их потенциальная энергия равна Eп.
Из (13) следует, что концентрация молекул максимальнав том месте, где их потенциальная энергия минимальна и наоборот.
Согласно (13) отношение концентраций молекул n1 и n2 в местах, где их потенциальная энергия равна соответственно Eп1 и Eп2 определяется соотношением:
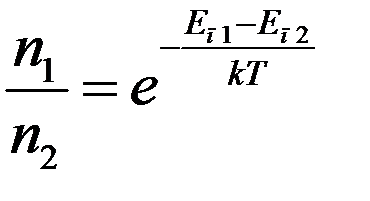 (14)
(14)
Очевидно, что поведение газа не изменится, если вместо силы тяжести на газ будет действовать другая консервативная сила, а выражение для потенциальной энергии будет иметь другой вид. Больцман показал, что формула (13) справедлива для газа, или любых других частичек, двигающихся хаотично и находящихся в любом потенциальном поле сил. Поэтому распределение (13) называется распределением Больцмана.
Закон Максвелла определяет распределение молекул по значениям их кинетической энергии (по скоростям), а закон Больцмана распределение молекул по значениям потенциальной энергии. Для этих распределений характерно наличие экспоненциального множителя, в показателе которого стоят отношения кинетической (Максвелл) или потенциальной (Больцман) энергии к величине пропорциональной средней энергии теплового движения молекул (kT).
Эти распределения можно объединить в один закон - распределение Максвелла–Больцмана. Если в формулу распределения Максвелла подставить n из (13), то получится распределение Максвелла–Больцмана:
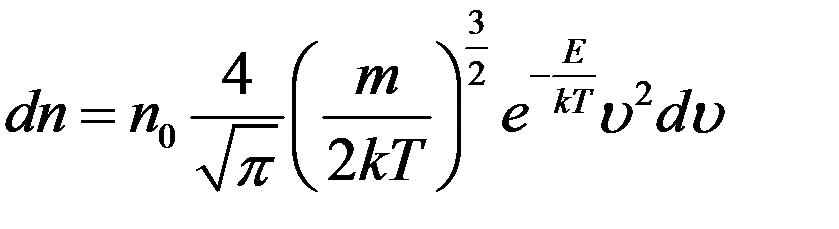 (15)
(15)
где
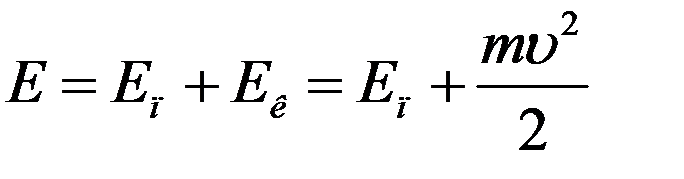
полная энергия молекулы в потенциальном поле сил, no - концентрация молекул в том месте, где их потенциальная энергия равна нулю, dn - концентрация молекул, которые обладают скоростями от υ до υ+dυ и потенциальной энергией Eп. Кинетическая энергия молекул зависит от скорости, потенциальная энергия зависит от их координат. Следовательно, распределение Максвелла–Больцмана одновременно учитывает, как и вероятность данного значения энергии, так и вероятность данного положения (координат) молекулы в потенциальном поле сил.
Распределение Больцмана легло в основу опытов Перрена по определению числа Авогадро и постоянной Больцмана. Броуновские частички ведут себя подобно большим молекулам. Следовательно, на них должно распространяться распределение Больцмана, т.е. броуновские частички в поле силы тяжести должны распределяться по высоте по закону (13).
Перрен изготовил эмульсию, содержавшую частички практически одинакового размера. Эмульсия помещалась в плоскую кювету, глубиной ~ 1 мм и рассматривалась через короткофокусный микроскоп (рис.3).
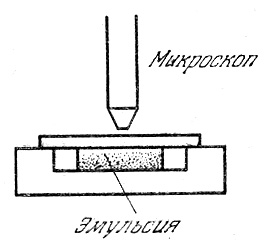
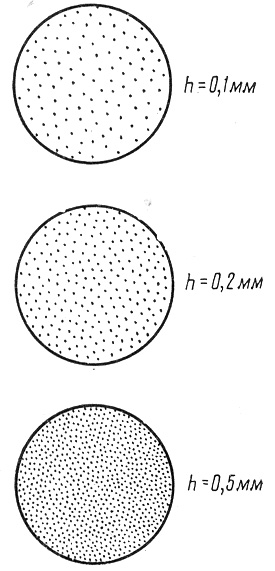
Рис.3. Схема опыта Перрена.
Микроскоп имел такую малую глубину резкости, что позволял наблюдать только те частицы, которые находились в слое толщиной ~ 1мкм = 10-6м. Перемещая микроскоп по вертикали можно было исследовать распределение частичек по высоте (рис.3). Число частичек, которые попали в поле зрения, очевидно, пропорционально их концентрации n. Тогда закон Больцмана для броуновских частичек имеет вид:
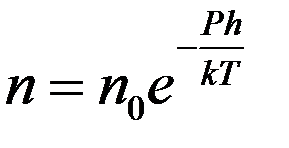
где no – концентрация частичек на высоте h = 0, n – концентрация частичек на высоте h, P – вес частички в эмульсии (с учетом силы Архимеда). Для двух разных высот h1 и h2 получим:
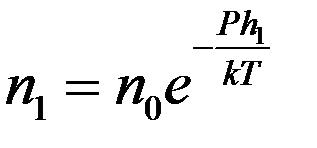 ,
, 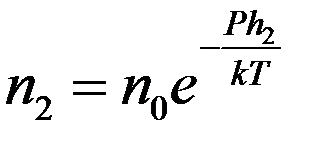
Отсюда:
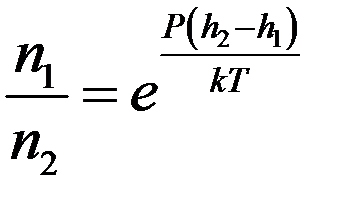
Прологарифмируем последнее уравнение:
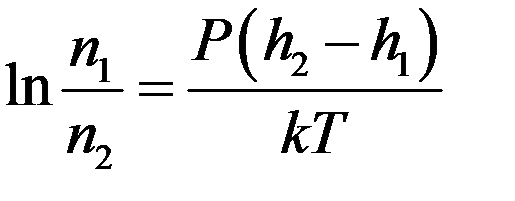
Отсюда:
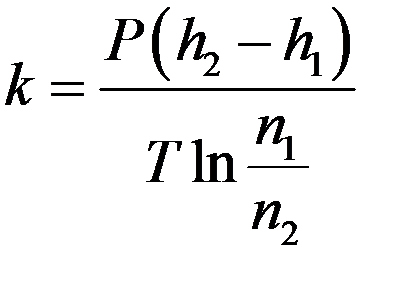
где
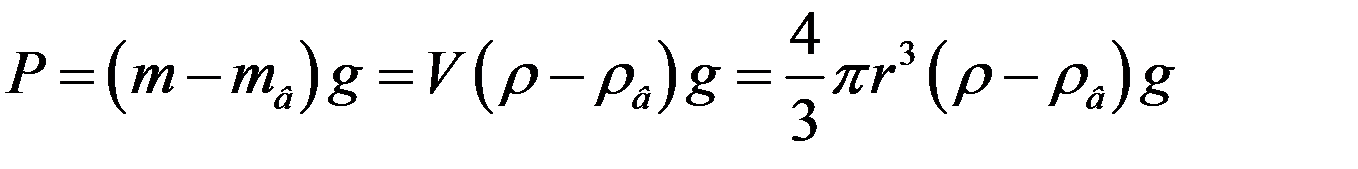
Окончательно:
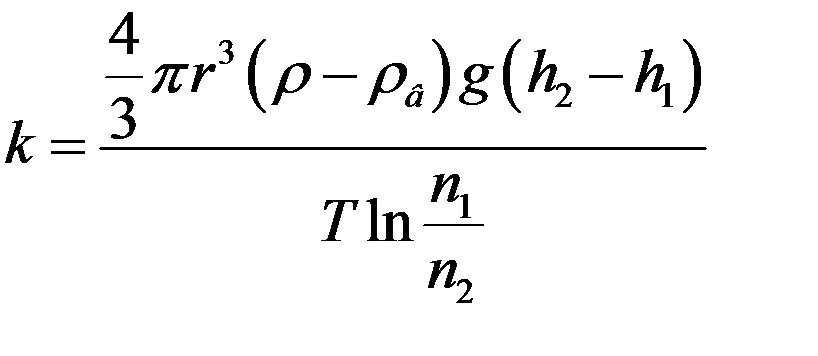
где ρ – плотность частички, ρв – плотность жидкости, r – радиус частички.
Определив r, ρ, и ρв, число частичек n1 и n2 на высотах h1 и h2 и, зная температуру можно рассчитать значение постоянной Больцмана и числа Авогадро (NА = R/k).
Полученное Перреном значение NА находилось в пределах (6,5 – 7,2)·1023 моль-1. Другие ученые, используя этот же метод, получили более точное значение NА:
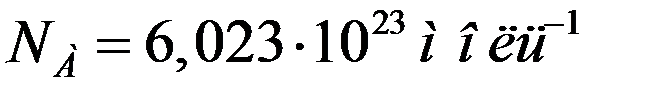 .
.
Дата добавления: 2017-09-01; просмотров: 1901;











