Зависимость физико-химических свойств кристаллических веществ от удельной энергии ионной кристаллической решетки
Приведенный в данном разделе материал свидетельствует о том, что весьма широкий спектр физико-химических свойств кристаллов может быть количественно описан с позиций энергии межатомного взаимодействия в ионном приближении, а предлагаемые удельные параметры энергии ионной кристаллической решетки - есть адекватная для описания свойств кристаллов форма ее выражения. Модифицируя таким путем концепцию кристаллической ионной решетки (первый энергетический подход к описанию свойств кристаллов), можно, выражаясь образно, вдохнуть новую жизнь в геоэнергетическую теорию Ферсмана и продемонстрировать ее новые возможности в современной науке.
Многочисленные работы последних десятилетий по экспериментальному распределению электронной плотности в кристаллах (Blaha, Redinger, Schwarz, 1984; Зуев, 1990; Matsuhata, Gjonnes, Tafto, 1994 и др.) свидетельствуют в пользу реальности довольно высоких эффективных зарядов атомов в оксидах и других соединениях (например, Li3+0.93N-2.8, Na+0.9Cl-0.9, Ca+1.8F2-0.9, Mg+1.8O-1.8, Cd+1.7O-1.7, Al2+2.4O3-1.6, Th+3.44O2-1.72, Sn+3.0O2-1.5 и т. д.). Довольно высокие эффективные заряды атомов в островных и цепочечных силикатах были получены в результате расчетов электронной плотности во многих работах японских ученых.
Как известно, одним из наиболее распространенных минералов земной коры является кварц SiO2, который уже стало традиционным рассматривать ионно-ковалентным кристаллом с 50% ионности и соответственно с зарядами Si+2O2-1. Однако целая группа экспериментальных и теоретических исследований, включающих строгие современные квантово-химические расчеты, нередко дают для кристаллических модификаций кремнезема с тетраэдрической координацией кремния более высокие эффективные заряды - вплоть до Si+3O2-1.5 с параметром fi = 0,75 (Julg, 1978; Li, Ching, 1985; Лазарев, Миргородский, Смирнов, 1985; Schobert, Dorner, 1994). Соответственно кристаллы с большей, чем в случае SiO2, разностью электроотрицательностей атомов должны считаться еще более ионными. Например, по данным (Sousa, Illas, 1993; Yourdshahyan, 1999) корунд является практически ионным соединением, обладая очень высокими эффективными зарядами атомов - Al2+2.7O3-1.8. Анализ спектров ионов Fe2+ в железосодержащем пиропе (Mg,Fe)3Al2Si3O12 также привел к выводу о весьма высокой ионности этого граната с эффективным зарядами атомов железа QFe = +1,9e и кислорода QO = -1,7e (Shen Guo-Yin, Zhao Min Guang, 1984).
В настоящее время, по-видимому, общепринятыми являются представления о том, что кристаллические галоиды щелочных и щелочноземельных металлов можно рассматривать как почти чисто ионные соединения, к которым концепция ионной кристаллической решетки безусловно применима (Урусов, 1975). В противовес общепринятому мнению есть данные в пользу весьма высоких эффективных зарядов атомов даже в таких, обычно трактуемых как ковалентные, кристаллах, как сфалерит - Zn+1.7S-1.7 (fi = 0,85)[1] (Julg, 1978; Кузнецов, 1979; Pillai, 1982).
Критики корректности концепции энергии кристаллической решетки применительно к оксидам базируются на энергетической невозможности (нереальности) свободных ионов O2-. Однако эффект стабилизации кристаллическим полем делает их вполне реальными (Урусов, 1975).
Все эти и другие соображения являются серьезными аргументами в пользу приемлемости концепции энергии кристаллической решетки даже в случае соединений поливалентных ионов. Точнее, можно говорить о том, что базирующаяся на ионном распределении зарядов в кристаллах концепция энергии кристаллической решетки довольно часто может рассматриваться в качестве вполне удовлетворительного приближения к действительности.
Методы оценки энергии ионных кристаллических решеток изложены во многих работах и, в частности, в работах (Ферсман, 1958; Бокий, 1971; Урусов, 1975, Современная кристаллография, 1979). В настоящей работе будет использован наиболее простой метод расчета энергии решетки суммированием энергетических коэффициентов (ЭК) составляющих кристалл ионов по А. Е. Ферсману:
U кДж/моль = 1071,5ΣЭК.(2.29)
Признавая весьма грубый, ориентировочный характер оценок U кристаллов в рамках данного метода, мы, тем не менее, остановились именно на нем, так как он удобен при массовых вычислениях и применим к соединениям любой сложности состава и структуры, поскольку не требует знания констант Маделунга, коэффициентов межатомного отталкивания и других параметров, используемых в более строгих современных методах (в том числе, квантово-механических) расчета энергии решетки.
Приемлемость результата оценок U по Ферсману подтверждается данными таблицы 2.1 для кристаллов состава Al2SiO5.
Другой пример взят нами непосредственно из книги А. Е. Ферсмана (Ферсман, 1958, стр. 122) (таблица 2.2).
Приведенные в этих таблицах примеры доказывают согласие оценок энергии решеток по методу Ферсмана как с современным компьютерным моделированием структур кристаллов (Урусов, Оганов, Еремин, 1998), так и с классическими термохимическими круговыми процессами (циклами) Борна-Габера.
Таблица 2.1
Энергии решеток для кристаллических соединений состава Al2SiO5
| Модификация состава Al2SiO5 | U, кДж/моль по (Ферсман, 1958) | U, кДж/моль по (Урусов и др., 1998) | Расхождение, Δ% |
| Кианит | 28126,9 | 27828,4 | +1,07 |
| Андалузит | 28126,9 | 27917,7 | +0,75 |
| Силлиманит | 28126,9 | 27912,8 | +0,77 |
Таблица 2.2
Энергии кристаллических решеток для некоторых
оксидов четырехвалентных металлов
| Кристалл состава МО2 | U, кДж/моль расчет по Ферсману | U, кДж/моль эксперимент (по циклу Борна-Габера) | Расхождение, Δ% |
| SiO2 | -3,25 | ||
| TiO2 | +0,06 | ||
| MnO2 | +0,03 | ||
| MoO2 | -0,11 | ||
| SnO2 | +0,14 | ||
| PbO2 | -0,07 |
Обычно энергию кристаллической решетки относят к единице количества вещества (молю) и выражают в ккал/моль или в кДж/моль. Однако очевидно, что для корректного сопоставления энергии решеток различных простых и сложных по составу соединений необходимо пользоваться удельными энергиями решеток, отнесенными к единице массы (1 г) или к единице объема (1 см3) вещества кристалла. Переход от U кДж/моль к удельной массовой энергии решетки Um кДж/г и удельной объемной энергии решетки Uv кДж/см3 осуществляется посредством формул:
Um = U/M; (2.30)
Uv = U/V, (2.31)
где M - формульный (мольный) вес соединения, г/моль; V - его мольный объем, см3/моль, определяемый по формуле V = M/ρ, где ρ- плотность вещества, г/см3.
Отсюда следуют указанные размерности Um и Uv и важное соотношение между ними:
Uv = Umρ. (2.32)
Для кварца U(SiO2) = 1071,5(8,6 + 1,55x2) = 12536,55 кДж/моль, M = 60,1 г/моль и ρ = 2,65 г/см3. По формулам (2.30) и (2.31) Um(SiO2) = 208,6 кДж/г и Uv(SiO2) = 552,8 кДж/см3.
Для такого сложного минерала, как берилл Be3Al2Si6O18, энергия кристаллической решетки по сумме эков составляющих ионов
U = 1071,5(2,65x3 + 4,95x2 + 8,6x6 + 1,55x18) = 104310,5 кДж/моль, M = 537,55 г/моль и r = 2,66 г/см3. Тогда по формулам (2.30) и (2.31) для берилла имеем Um = 194,05 кДж/г и Uv = 516,2 кДж/см3.
Аналогичные расчеты для мусковита KAl2[AlSi3O10](OH)2 дают U = 1071,5(0,36 + 4,95x3 + 8,6x3 + 1,55x12 + 1,1x2) = 66229,4 кДж/моль и далее, используя M = 398,4 г/моль и ρ = 2,8 г/см3, получаем Um = 166,3 кДж/г и Uv = 465,6 кДж/см3.
Обратим внимание на то, что при колоссальном различии кварца, берилла и мусковита по параметрам общих (мольных) энергий кристаллических решеток, они оказались довольно близкими, сопоставимыми по удельным параметрам Um и Uv, чем и объясняется, по-видимому, обычный парагенезис этих минералов в пегматитах, грейзенах и других породах. Поэтому в дальнейшем при решении проблемы выявления корреляционных зависимостей свойств кристаллов от энергетических параметров были использованы именно удельные энергии кристаллических решеток.
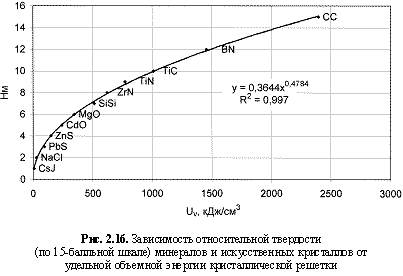
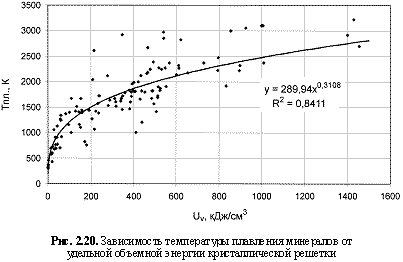
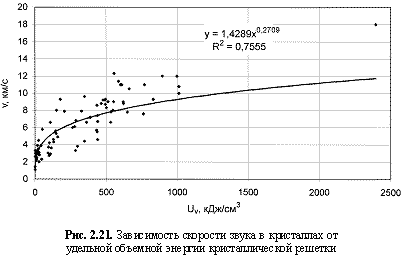
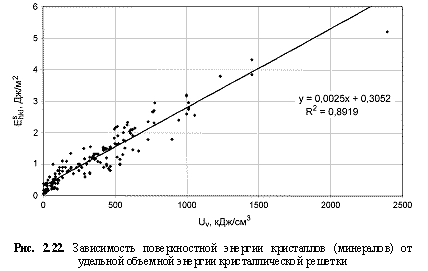
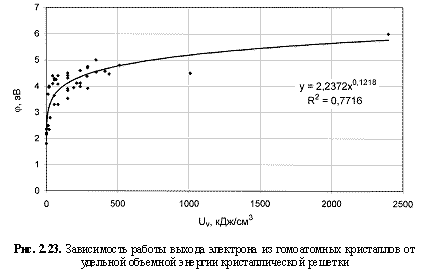
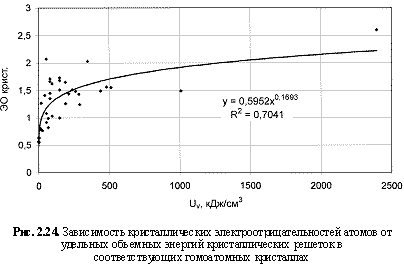
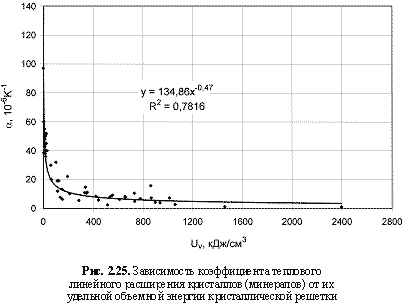
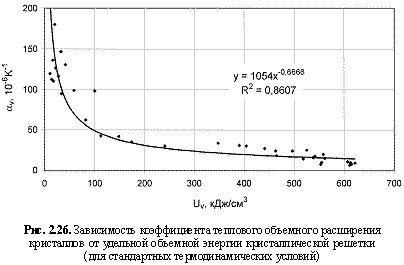
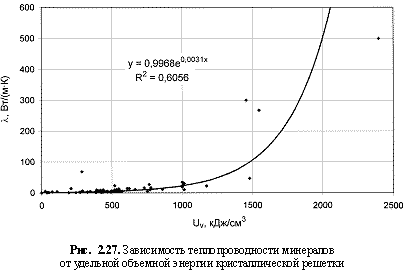
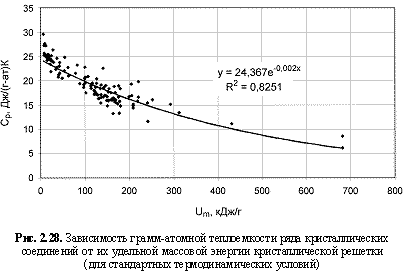
Соответствующий графический материал в координатах «Uv(Um)/свойство кристалла» с выводом большинства формул представлен на рис. 2.16-2.29. Обобщая материал по выведенным аналитическим зависимостям, можно сделать следующие выводы:
1. Твердость кристаллов (минералов) - относительная (НМ) и абсолютная (микротвердость по Викерсу HV, кгс/мм2), модуль Юнга (Е, ГПа), температура плавления (Тпл., К), скорость звука (v, км/с), поверхностная энергия (Eshkl, Дж/м2), работа выхода электрона из гомоатомных, в основном металлических кристаллов (φ, эВ), кристаллическая электроотрицательность (ЭОкрист.), коэффициенты теплового линейного (α1, 10-6×K-1), объемного (αv, 10-6xK-1) расширения и сжимаемости (β, 10-12×Па-1), теплопроводность (λ, Вт/м×K), показатель преломления (n), коэффициент трещиностойкости (К1с, МПа×м0.5), эффективная энергия разрушения (γ, Дж/м2) лучше коррелируются с параметрами Uv, нежели с параметрами Um, о чем, как показали расчеты, свидетельствуют более высокие величины достоверности аппроксимации R2 соответствующих зависимостей. В связи с этим предлагаются следующие формулы количественной оценки указанных свойств кристаллических веществ:
HM = 0,364Uv0.48; (2.33) * по 15 бальной системе
HM = 0,39Uv0.465; (2.34)
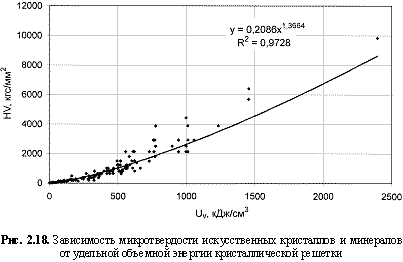
HV = 0,21Uv1.37; (2.35)
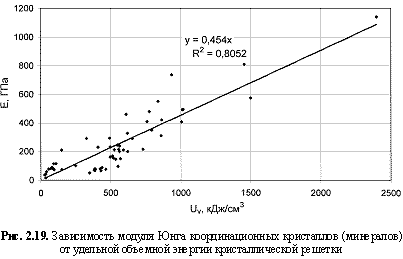
E = 0,45Uv; (2.36)
G = 1,437Uv0.675; (2.37)
K = 3,7Uv0.6; (2.38)
Тпл. = 290Uv0.31; (2.39)
v = 1,43Uv0.27; (2.40)
Eshkl = 0,0025Uv + 0,3; (2.41)
φ = 2,24Uv0.122; (2.42)
ЭОкрист. = 0,6Uv0.17; (2.43)
αl = 135Uv-0.47; (2.44)
αv = 1054Uv-0.67; (2.45)
β = 407,4Uv-0.693; (2.46)
λ = 1,0е0.003Uv; (2.47)
n = 0,0004Uv + 1,42; (2.48)
K1c = 0,7e0.0015Uv; (2.49)
γ = 0,027Uv. (2.50)
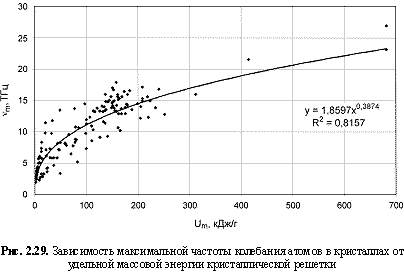
2. Грамм-атомная теплоемкость (Ср, Дж/(г-ат)×K) и частота максимального колебания атомов (nm, ТГц) в кристаллах лучше коррелируются с параметрами Um, в связи с чем предлагаются формулы количественной оценки этих двух свойств кристаллических веществ:
Ср = 24,37e-0.002Um; (2.51)
nm = 1,86Um0.39. (2.52)
При выводе формул (2.33)-(2.52) был использован тот же самый обширный материал по физико-химическим свойствам минералов и искусственных (в том числе тугоплавких) кристаллов, что и в случае выявления искомых зависимостей по параметрам структурной рыхлости ω. Поэтому соответствующие источники и ссылки по свойствам веществ указаны в предыдущем разделе 2.1. Массивы табличных данных, использованных при построении графиков, не приводятся, так как эти данные включают многие сотни кристаллов - простых гомоатомных, бинарных, а также разнообразных сложных соединений (оксидов, силикатов, сульфатов, карбонатов и др.).
Формулы твердости (2.33), (2.34) и (2.35) относятся в основном к кристаллам с координационным и каркасным мотивами структуры и не применимы к анизодесмическим соединениям, характеризующимся резко выраженным островным, цепочечным, либо слоистым мотивом структуры. Впрочем, как показано в разделе 2.2.1, расчет твердости анизодесмических (например, островных) кристаллов возможен, если параметры Uv рассчитываются с учетом их структурного мотива.
Ковалентные кристаллы (алмаз и кремний) в соответствии с представлениями Э. Фридриха, А. Е. Ферсмана, Н. В. Белова[2], А. С. Поваренных допустимо аппроксимировать как ионные (С4+С4-, Si4+Si4-). Получившаяся в результате четкая зависимость НМ = f(Uv) на рис. 2.16 подтвердила правомерность такого подхода к ковалентным соединениям. Здесь уместно привести касающуюся твердости веществ цитату Э. Фридриха (Ферсман, 1958, стр. 193): «Электростатическое притяжение атомов является, таким образом, причиною твердости тела... атомные решетки ведут себя так, как если бы они были ионными».
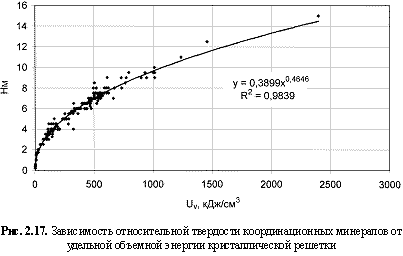
В отношении твердости металлов аналогичный подход был успешно использован А. С. Поваренных в монографии (Поваренных, 1963). Резкое расширение массива данных с включением более 200 объектов (рис. 2.17) лишь незначительно изменило первоначальную формулу (2.33), выведенную по 12 эталонам усовершенствованной 15-балльной шкалы Мооса (рис. 2.16). Поэтому при оценке относительной твердости кристаллов допустимо пользоваться любой из формул (2.33) или (2.34).
Как известно (Бокий, 1971), концепция энергии кристаллической решетки в приложении к металлам базируется на представлении о взаимодействии локализованных в узлах решетки положительных атомных остовов (Мn+) c делокализованным в межостовном пространстве электронным газом (ne-). Данные по величинам энергетических коэффициентов электронного газа металлических кристаллов пока отсутствуют, поэтому прямые расчеты соответствующих энергий решеток металлов по методу Ферсмана не представляются возможными. В этих случаях пришлось обратиться к косвенному методу оценки Uv металлов - по формуле (2.34) с использованием известных валентностей металлов и их относительной твердости (Поваренных, 1963). Найденные таким путем величины Uv гомоатомных металлических кристаллов были использованы при выводе формул (2.42) и (2.43). Формула теплопроводности (2.47) относится к диэлектрикам, т. е. к соединениям с большой шириной запрещенной зоны (Eg), обладающим ковалентными, ионными и ионно-ковалентными связями. Необходимо также подчеркнуть, что получаемые по формулам (2.44)-(2.47), (2.51) параметры относятся к веществам, находящимся в стандартных термодинамических условиях.
Из вышеизложенного следует, что на базе параметров удельных энергий кристаллических решеток имеется возможность количественного объяснения и предсказания весьма широкого спектра физико-химических свойств кристаллов (минералов), включая прочностные (механические) и упругие, теплофизические, термические, электрические (термоэмиссионные), кристаллохимические и т. д. и т. п.
Достоверность выявленных зависимостей базируется на использовании при их выводе весьма представительных статистических материалов, включающих соответствующие корреляционные данные для многих сотен кристаллических соединений. Необходимо подчеркнуть, что средняя величина достоверности аппроксимации установленных зависимостей оказалась довольно высокой: <R2> = 0,83 при ее колебании в интервале от 0,64 до почти 1 (рис. 2.16). И столь высокие коэффициенты корреляции получились при использовании весьма грубых оценок энергий решеток по Ферсману. Применение в дальнейшем более совершенных методов расчета энергии кристаллических решеток, несомненно, приведет к уточнению установленных зависимостей и росту соответствующих им параметров R2.
Обобщая приведенный материал данного раздела, можно сделать следующие выводы. Если вместо общей энергии кристаллической решетки оперировать удельными энергиями кристаллической решетки, отнесенными к единичной массе или единичному объему вещества кристалла, то неожиданным образом выявляется глубокая, закономерная взаимосвязь указанных удельных энергетических характеристик кристалла с широким спектром его самых разнообразных физико-химических свойств. По нашему мнению, эта закономерность может трактоваться как имеющая фундаментальный характер, поскольку убедительно доказывает, что разные физико-химические свойства твердых тел (механические, упругие, термические, теплофизические, кристаллохимические и др.) в действительности определяются единой природой - энергией взаимодействия составляющих кристалл ионов, а удельные энергии кристаллической решетки (параметры Uv, реже Um) являются адекватной для количественного описания свойств веществ формой выражения энергии решетки.
Другим нетривиальным следствием данного раздела является то обстоятельство, что гомоатомные ковалентные и металлические кристаллы в рамках данного энергетического подхода при оценке их свойств могут рассматриваться как квазиионные, к которым предлагаемые формулы также применимы. В отношении твердости эта закономерность была установлена, как указано выше, еще в работах Э. Фридриха, А. Е. Ферсмана, А. С. Поваренных, однако в настоящем исследовании она получила дальнейшее убедительное подтверждение в отношении многих других свойств атомных кристаллов при оперировании именно удельными энергиями кристаллических решеток.
Немаловажно также фактическое возрождение геоэнергетической теории А. Е. Ферсмана, которая в модифицированном виде (удельных энергий решеток) может дать современной геологической науке весьма полезные и ценные результаты по объяснению совместного нахождения (парагенезисов) минералов в горных породах и рудах, а также энергетической направленности смены (замещения) одних минеральных ассоциаций другими в различных геологических процессах. Удельные энергии кристаллических решеток минералов являются, по нашему мнению, объективной мерой их энергетической стабильности. Заметим, кстати, что использование последних опровергает вывод работы В. С. Урусова и др. (Урусов, Оганов, Еремин, 1998) о неустойчивости кианита (как известно, наиболее стабильной модификации Al2SiO5) с точки зрения величины энергии кристаллической решетки. В самом деле, рассчитанные удельные энергии решеток модификаций Al2SiO5 (Uv кианита = 601 кДж/см3, Uv андалузита = 534 кДж/см3, Uv силлиманита = 551 кДж/см3) однозначно свидетельствуют о максимальной стабильности именно кианита. Точно такой же порядок роста стабильности (андалузит→силлиманит→кианит) следует из данных по энергоплотности этих соединений (соответственно 94,8 кДж/см3, 99,3 кДж/см3 и 112,3 кДж/см3).
Другой весьма характерный пример, приводимый В. С. Урусовым (Урусов, 1975, стр. 270) с целью дискредитации концепции энергии кристаллической решетки. Известно, что первые порции оливина (Mg,Fe)2SiO4 всегда богаче магнием, а более поздние железом, т. е. кристаллизация идет в последовательности Mg2SiO4→Fe2SiO4, в которой понижаются температуры плавления (2163°К и 1478°К соответственно у форстерита и фаялита). Но порядок энергий решеток обратный: U(Mg2SiO4) = 20639,7 кДж/моль и U(Fe2SiO4) = 20761 кДж/моль. Однако при использовании удельных объемных энергий кристаллических решеток: Uv(Mg2SiO4) = 469,4 кДж/см3 и Uv(Fe2SiO4) = 448,4 кДж/см3 все становится на свои места - как в смысле соответствия с указанными температурами плавления, так и в смысле относительной твердости, заметно большей у форстерита по сравнению с фаялитом.
Такая же ситуация имеет место для другой пары минералов - энстатита Mg2Si2O6 и ферросилита Fe2Si2O6 с обратным соотношением величин общих и удельных объемных энергий кристаллических решеток: U(Mg2Si2O6) = 30543,6 кДж/моль и U(Fe2Si2O6) = 31355,9 кДж/моль, Uv(Mg2Si2O6) = 486,4 кДж/см3 и Uv(Fe2Si2O6) = 475,3.
И последний пример «дискредитации» концепции ионной кристаллической решетки применительно к полевым шпатам - альбиту NaAlSi3O8 и анортиту CaAl2Si2O8 (Урусов, 1975). По оценкам В. С. Урусова энергия решетки альбита гораздо выше по сравнению с анортитом, что находится в явном противоречии с более высокой температурой плавления последнего.[3] Для выхода из этой ситуации при оперировании энергиями решеток по Ферсману достаточно несколько изменить некоторые из стандартных энергетических коэффициентов ионов, входящих в состав этих минералов, а именно принять их равными: Na - 0,45; Ca - 1,75; Al[4] - 6,5; Si - 7,3; O - 1,55. Изменения касаются повышения энергетического коэффициента иона алюминия в тетраэдрической координации[4] и принятия энергетического коэффициента иона кремния по Шибольду (Сауков, 1955, с. 161). Тогда расчеты по формулам (2.29), (2.30), (2.31) дают для альбита NaAlSi3O8: U = 44199,4 кДж/моль, Um = 168,54 кДж/г, Uv = 441,6 кДж/см3 и для анортита CaAl2Si2O8: U = 44735,12 кДж/моль, Um = 160,77 кДж/г, Uv = 443,72 кДж/см3. Полученные данные по величинам удельных объемных энергий кристаллических решеток альбита и анортита находятся в согласии с их температурами плавления и величинами энергоплотности - большей у анортита (78,91 кДж/см3) и меньшей у альбита (76,98 кДж/см3) (Зуев, Денисов, Мочалов и др., 2000). Корректность величины ЭК Al[4] = 6,5 можно проверить по другим кристаллическим соединениям с тетраэдрической координацией алюминия. Так, для кристалла AlN (d = 1,89 Å, r = 3,28 г/см3) U(AlN) = 1071,5(6,5 + 3,6) = 10822,15 кДж/моль, Um(AlN) = 263,91 кДж/г, Uv(AlN) = 865,6 кДж/см3, и расчет по формуле (2.32) дает НМ = 9,4 (экспериментальная относительная твердость равна 9-10). Аналогичным образом для кристалла AlSb в случае принятия ЭК Al[4] = 6,5 имеем Uv(AlSb) = 283 кДж/см3 и НМ = 5,4 в близком согласии с экспериментом (Поваренных, 1963).
Приведенные примеры дают возможность реабилитировать концепцию энергии кристаллической ионной решетки и тем самым подтвердить ее полезность при объяснении физических свойств минералов.
Помимо чисто научного, теоретико-познавательного значения данный раздел имеет также несомненный практический выход - как разработка нового эффективного метода количественной оценки многих физико-химических свойств кристаллического вещества, экспериментальное определение которых по ряду причин затруднено или невозможно. К тому же для многих кристаллов приводимые в справочной литературе данные по физико-химическим свойствам нередко противоречивы и требуют уточнения. Рассмотрим конкретный пример - кристалл CdO (минерал имеет названия монтепонит или кадмоксит), обладающий кубической структурой типа NaCl. Вычислив для кристалла CdO энергетические параметры U = 3804 кДж/моль, Um = 29,6 кДж/г и Uv = 243 кДж/см3, по соответствующим формулам можно количественно охарактеризовать более десятка свойств этого соединения (Зуев, Денисов, Мочалов и др., 2000). Полученные для кристалла CdO данные доказывают полезность использования удельных энергий кристаллической решетки при оценке свойств кристаллов. Обратим внимание на то, что ряд важных физико-химических свойств кристалла CdO в справочной литературе отсутствует, другие же требуют уточнения. В частности, приводимая во всех основных минералогических справочниках относительная твердость кадмоксита (около 3) является ошибочной, явно заниженной, что связано, по-видимому, с ее определением в дезинтегрированных порошковатых массах минерала. Уточненная нами относительная твердость кристалла CdO (5) подтверждается независимыми расчетами по формулам А. С. Поваренных (Поваренных, 1963) и В. В. Зуева (Зуев, 1990).
Особую ценность представляет возможность прогнозирования широкого спектра физико-химических параметров для вновь создаваемых неорганических материалов. Другими словами, введенная нами концепция удельной энергии кристаллической решетки может оказать существенную помощь в решении актуальной проблемы синтеза веществ с заданными свойствами - в плане их прогнозирования.
В качестве резюме данного раздела отметим следующее. Признавая главенствующую, ведущую роль и более универсальный характер второго энергетического подхода (энергоплотности) в объяснении и предсказании свойств твердых тел (Зуев, Денисов, Мочалов, 2000), нельзя игнорировать также большие возможности в этой области, открываемые использованием первого энергетического подхода в виде удельных энергий кристаллических решеток. А совместное использование различных энергетических подходов дает возможность получения более надежных результатов по прогнозируемым свойствам твердых тел. Подробнее этот вопрос будет рассмотрен в заключительной части 2-ой главы.
Завершая раздел, рассмотрим вопрос о количественной оценке комплексности весьма распространенных сложных минералов, содержащих различные группировки (радикалы), обуславливающие соответствующие (островные) структурные мотивы и влияющие на свойства (твердость и др.) таких минералов. Следует подчеркнуть, что постановка и решение этого вопроса оказались возможными лишь в рамках концепции энергии кристаллической решетки, которая в этом отношении обладает несомненным преимуществом по сравнению с другими энергетическими подходами.
[1] Если принять во внимание весь накопившийся к настоящему времени соответствующий материал, то большинство данных по эффективным зарядам атомов в сфалерите укладывается в следующем диапазоне: Q(Zn) = +(1,2±0,5), Q(S) = -(1,2±0,5).
[2] По мнению академика Н. В. Белова (Белов, 1947, стр.66) ковалентную связь в алмазе с позиций квантовой механики можно трактовать как результат резонанса (непрерывной осцилляции) предельно-ионных структур С4+С4- <-> С4-С4+.
[3] В то время как параметры энергии атомизации альбита и анортита находятся в соответствии с их температурами плавления.
[4] Энергетический коэффициент иона алюминия в наиболее распространенной для него октаэдрической координации примем равным 4,95 (Ферсман, 1958). По определению ЭК иона обратно пропорционален ионному радиусу, т. е. величине 1/ri. Согласно (Бацанов, 1991), октаэдрический и тетраэдрический радиусы иона Al3+равны 0,54 Å и 0,39 Å. Тогда из соответствующей пропорции ЭК Al3+ = (4,95x1/0,39)/(1/0,54) = 6,8. По другим данным (Урусов, 1975; Современная кристаллография, 1979) ri(Al[6]) = 0,67 Å, ri(Al[4]) = 0,53 Å и ЭК Al3+ = (4,95x1/0,53)/(1/0,67) = 6,3. Другой подход: для атомов в тетраэдрической координации (КЧ = 4) расчеты электроотрицательностей согласно (Яковлев, 2002) дают ЭО Al = 1,63 и ЭО Si = 1,86. Полагая прямо пропорциональную зависимость между ЭК и ЭО соответствующих ионов (атомов) и приняв ЭК Si4+ = 7,3, из пропорции находим для тетраэдрической координации ЭК Al3+ = (7,3x1,63)/1,86 = 6,4.
Дата добавления: 2017-09-01; просмотров: 1628;











