Постановка краевой задачи. Метод стрельбы.

Краевая задача – задача отыскания частного решения системы

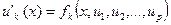(12), 1 ≤ k ≤ p, на отрезке a ≤ x ≤ b, на котором дополнительные условия налагаются на значения функции u_k(x) более чем в одной точке этого отрезка. В качестве примера моно привести задачу нахождения статического прогиба u(x) нагруженной струны с закрепленными концами:

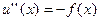, a ≤ x ≤ b, u(a) = u(b) = 0. Здесь f(x) имеет смысл внешней изгибающей нагрузки на единицу длины струны, деленной на упругость струны.

Найти точное решение краевой задачи в элементарных функциях удается редко: для этого надо найти общее решение системы (12) и суметь явно определить из краевых условий значения входящих в него постоянных. Одним из методов, предполагающих численное решение поставленной задачи, является метод стрельбы, в котором краевая задача для системы (12) сводится к задаче Коши для той же системы.

Рассмотрим систему двух дифференциальных уравнений первого порядка

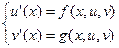(13)

с краевыми условиями

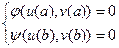(14)

Сначала выберем некоторое значение 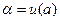, так что 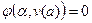. Это уравнение мы можем решить и определить 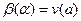. Таким образом у нас появились два числа 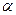и β, которые будут определять задачу Коши 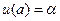, 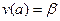для системы (13), удовлетворять левому краевому условию, но не удовлетворять второму уравнению (14). Тем не менее, решим систему ОДУ с задачей Коши каким-либо из известных нам численных методов. Получим решение вида

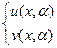(15), зависящее от 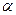как от параметра.

Теперь мы должны каким-либо способом менять параметр 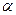до тех пор, пока не подберется такое значение, для которого будет выполнено условие 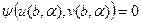(16), т.е. правое краевое условие. Для этого случайным образом берут значения 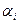до тех пор, пока среди величин 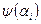не окажется разных по знаку.

Если это осуществилось, пара таких значений определяет интервал 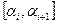, который можно обработать методом дихотомии до получения корня уравнения (16). Нахождение каждого нового значения функции (16) требует нового численного интегрирования для решения ОДУ, что делает этот метод достаточно медленным.