Метод Рунге-Кутты IV порядка.

Данная схема является наиболее употребительной. Здесь в разложении функции в ряд Тейлора учитываются члены до h⁴ включительно, т.е. погрешность на каждом шаге пропорциональна h⁵. Для практических вычислений используются следующие соотношения, обобщенные в данном случае на решение системы ОДУ:

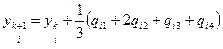, где i = 1…p, p – число уравнений в системе.

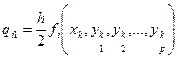; k – номер точки, для которой осуществляется расчет;

;

;

.

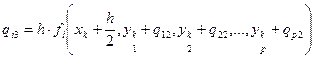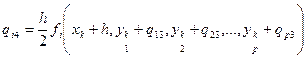К достоинствам метода следует отнести высокую точность вычислений. Схемы более высокого порядка точности практически не употребляются в силу своей громоздкости. Также немаловажно, что метод является явным, т.е. значение y_k+1 вычисляется по ранее найденным значениям за известное заранее число действий.

Все представленные выше схемы допускают расчет с переменным шагом. Например, шаг можно уменьшить там, где функция быстро изменяется, и увеличить в обратном случае. Так, метод Рунге-Кутты-Мерсона позволяет оценивать погрешность на каждом шаге и, в зависимости от полученной оценки принимать решение об изменении шага. Автоматический выбор шага позволяет значительно сократить время вычислений.