Метод Рунге-Кутты II порядка.

Увеличение точности решения ОДУ из предыдущей задачи при заданном шаге h может быть достигнуто учетом большего количества членов разложения функции в ряд Тейлора. Для метода Рунге-Кутты второго порядка следует взять три первых коэффициента, т.е. обеспечить:

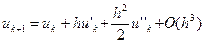. (8)

Переходя к приближенному решению y ≈ u и заменяя производные в (8) конечными разностями, получаем в итоге следующее выражение:

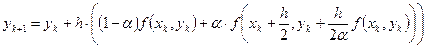, (9)

где 0 ≤ α ≤ 1– свободный параметр. Можно показать, что если f(x,u) непрерывна и ограничена вместе со своими вторыми производными, то решение, полученное по данной схеме, равномерно сходится к точному решению с погрешностью порядка h².

Для параметра α наиболее часто используют следующие значения:

1) α = 1. В этом случае

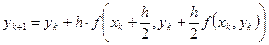. Графически это уточнение можно интерпретировать так: сначала по схеме ломаных делается шаг h/2, и находится значение 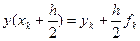. В найденной точке определяется наклон касательной к интегральной кривой, который и будет определять приращение функции для целого шага, т.е. отрезок [AB] (см. рисунок) будет параллелен касательной, проведенной в точке (x_k + h/2, y(x_k + h/2) ) к интегральной кривой.

2) α = ½. В этом случае

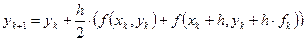. Можно представить, что в этом случае по методу Эйлера сначала вычисляется значение функции и наклон касательной к интегральной кривой в точке x_k+1. Затем находится среднее положение касательной из сравнения соответствующих наклонов в точках x_k и x_k+1, которое и будет использоваться для расчета точки y_k+1.