Меркаторская проекция

Предложенная Меркатором проекция относится к разряду нормальных цилиндрических равноугольных проекций.

Карты, построенные в этой проекции, называются меркаторскими, а проекция ® проекция Меркатора или меркаторская проекция.

В меркаторской проекции все меридианы и параллели прямые и взаимноперпендикулярные линии, а линейная величина каждого градуса широты постепенно увеличивается с возрастанием широты, соответственно растягиванию параллелей, которые все в этой проекции по длине равны экватору.

Проекция Меркатора по характеру искажений относится к классу равноугольных.

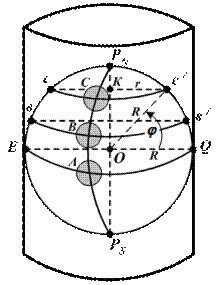
Для получения морской навигационной карты в проекции Меркатора условный глобус помещают внутрь касательного цилиндра таким образом, чтобы их оси совпали.

Затем проецируют из центра глобуса меридианы на внутренние стенки цилиндра. При этом все меридианы изобразятся прямыми, параллельными между собой и перпендикулярными экватору линиями. Расстояния между ними равны расстояниям между теми же меридианами по экватору глобуса. Все параллели растянутся до величины экватора. При этом параллели, ближайшие к экватору, растянутся на меньшую величину и по мере удаления от экватора и приближения к полюсу величина их растяжения увеличивается.

Закон растяжения параллелей (рис. 6.1).

а)

б)

в)

Рис. 6.1. Закон растяжения параллелей

R и r – радиус Земли и произвольной параллели (СС¢).

j – широта произвольной параллели (СС¢).

Из прямоугольного треугольника ОС¢К получим:

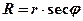(6.4)

Обе части равенства умножим на 2p, получим:

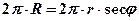(6.5)

где 2p × R – длина экватора;

2p × r – длина параллели в широте j.

Следовательно, длина экватора равна длине соответствующей параллели, умноженной на секанс широты этой параллели. Все параллели, удлиняясь до длины экватора, растягиваются пропорционально sec j.

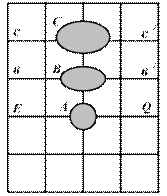
Разрезав цилиндр по одной из образующих, и развернув его на плоскость, получим сетку взаимно перпендикулярных меридианов и параллелей (рис. 6.1б).

Эта сетка не удовлетворяет требованию равноугольности, т.к. изменились расстояния между меридианами по параллели, ибо каждая параллель растянулась и стала равной длине экватора. В результате фигуры с поверхности Земли перенесутся на сетку в искаженном виде. Углы в природе не будут соответствовать углам на сетке.

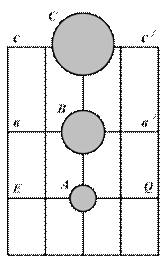
Очевидно, для того, чтобы не было искажений, т.е. чтобы сохранить на карте подобие фигур, а следовательно, и равенство углов, необходимо все меридианы в каждой точке растянуть на столько, на сколько растянулись в данной точке параллели, т.е. пропорционально sec j. При этом эллипс на проекции вытянется в направлении малой полуоси и станет кругом, подобным острову круглой формы на поверхности Земли. Радиус круга станет равным большой полуоси эллипса, т.е. будет в sec j раз больше круга на поверхности Земли (рис. 6.1в).

Полученная таким образом картографическая сетка и проекция будут полностью удовлетворять требованиям, предъявленным к морским навигационным картам, т.е. проекцией Меркатора.

<19 20 212223 24 25 >

Дата добавления: 2017-09-01; просмотров: 1877;

Поиск по сайту

Узнать еще