Изображение окружностей в аксонометрических проекциях

Построение окружности в прямоугольной изометрической проекции.

Изометрическими проекциями окружностей, расположенных в плоскостях проекций или плоскостях, параллельных им, являются эллипсы с одинаковыми соотношениями осей. Большие оси эллипсов равны 1,22D, а малые – 0,71 D, где – диаметр D изображаемой окружности (рис.13).

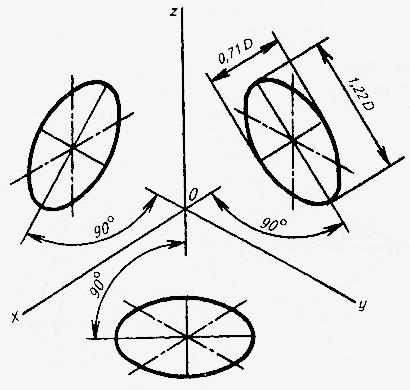
Рис.13

Направление осей эллипсов зависит от положения проецируемой окружности: большая ось эллипса всегда перпендикулярна к той аксонометрической оси, которой нет в плоскости заданной окружности, а малая ось совпадает с направлением этой оси. Например, окружность, лежащая в горизонтальной плоскости проекций, в изометрии проецируется в эллипс, большая ось которого перпендикулярна к оси z, а малая совпадает с направлением этой оси. На практике часто вместо эллипсов чертят овалы, состоящие из четырех дуг окружности. Рассмотрим два способа построения овала.

Первый способ - построение овала по большой оси АВ (рис.14). Построим в изометрической проекции окружность, расположенную во фронтальной плоскости проекций. Сначала построим изометрические оси х и z и прямые в направлении большой и малой осей эллипса. Затем проведем окружность, диаметр которой равен большой оси АВ (рис.14,а), и отметим точки 1и 2. Через точки пересечения осей х и z с окружностью и точки 1 и 2 проведем прямые, соединяющие эти точки (рис.14,б). Отметим в пересечении этих прямых с осью эллипса АВ точки 3 и 4. Точки1,2,3 и 4 являются центрами дуг овала. Из центров 3 и 4 проведем две малые дуги овала через точки А и В, а из центров 1 и 2 – две большие дуги через точку К (рис.14,в) Отношение осей полученного овала совпадает с отношением осей эллипса.

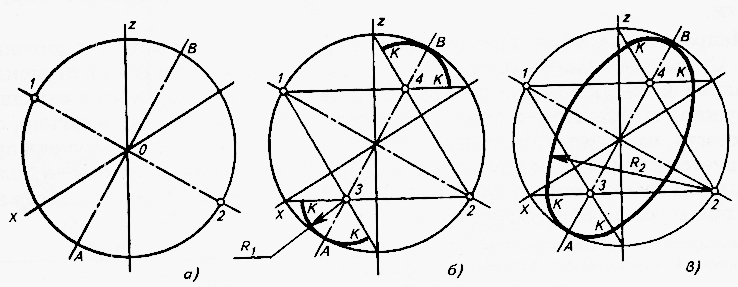
Рис.14

Второй способ – построение овала, вписанного в ромб (рис.15). Сначала строим ромб со стороной, равной диаметру окружности, и проводим через его центр большую и малую оси и два диаметра ac и bd эллипса (рис.15,а). Затем из вершин А и В тупых углов ромба проводим циркулем через точки a,c, b и d – пересечения диаметров эллипса со сторонами ромба – две большие дуги овала (R). Центры C и D малых дуг (r), замыкающих овал, находятся на большой оси эллипса. Чтобы их найти, проводим прямые через вершину В (или А) тупого угла ромба и точки a и b пересечения диаметров эллипса со сторонами ромба (рис.15,б).

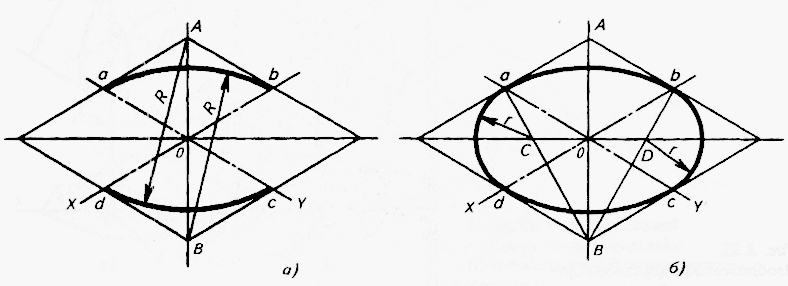
Рис.15

Построение окружности во фронтальной диметрической проекции.

Во фронтальной диметрической проекции окружность, лежащая в плоскости П2 изображается без искажения (рис.16). Окружности, спроецированные на плоскости П1 и П3, изображаются эллипсами, у которых большая ось равна 1,07D, а малая – 0,33D. Большая ось эллипса в плоскости П1 наклонена к горизонтали под углом 7˚14', а в профильной плоскости – под тем же углом к вертикали (рис.17).

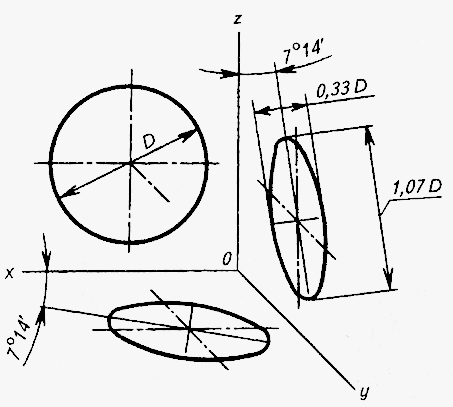
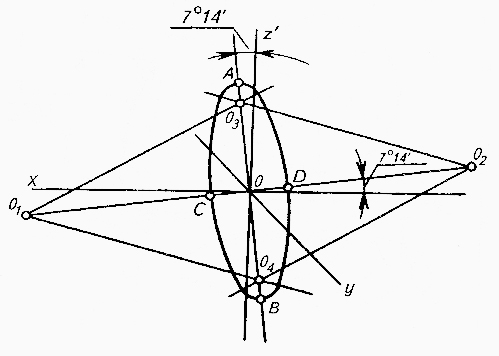
Рис.16 Рис.17

Построение окружности в прямоугольной диметрической проекции

В прямоугольной диметрии окружности проецируются в виде эллипсов, малые оси которых, как и в изометрии, параллельны осям, отсутствующим в плоскостях данных окружностей. Для эллипса, лежащего в горизонтальной плоскости, малая ось идет по направлению оси z, а большая – перпендикулярна к ней (рис.18).

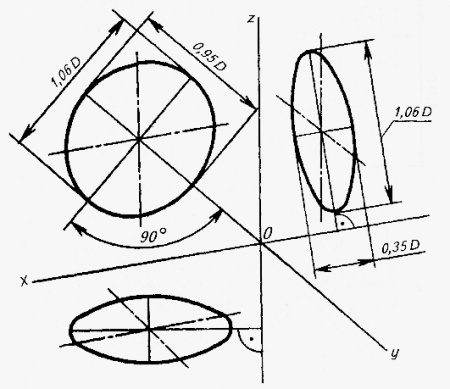
Рис.18

Длина большой оси для всех эллипсов одинаковая и равна 1,06D диаметра изображаемой окружности. Величина малой оси различна: для фронтальной плоскости проекций величина малой оси равна 0,95 – 0,95D длины большой оси, или 0,95 диаметра окружности; для горизонтальной и профильной плоскостей и для плоскостей, параллельных им, величина малой оси равна 1/3 большой оси, то есть 0,35 диаметра окружности.

На практике эллипсы заменяют четырехцентровыми овалами (рис.19). Рассмотрим пример построения окружности, расположенной параллельно плоскости П2 (рис.19,а). Через точку О – начало аксонометрических осей - проводим оси, параллельные осям x и z. Из центра О, радиусом, равным радиусу данной окружности, проводим вспомогательную окружность, которая пересекается с осями в точках 1,2,3.4. Из точек 1 и 3 (по направлению стрелок) проводим горизонтальные линии до пересечения с осями АВ и СД овала и получаем точки О1,О2,О3.О4. приняв за центры точки О1 и О4 радиусом R, проводим дуги 1-2 и 3-4. Приняв за центры точки О2 и О3, проводим радиусом R1 дуги овала2-3 и 1-4.

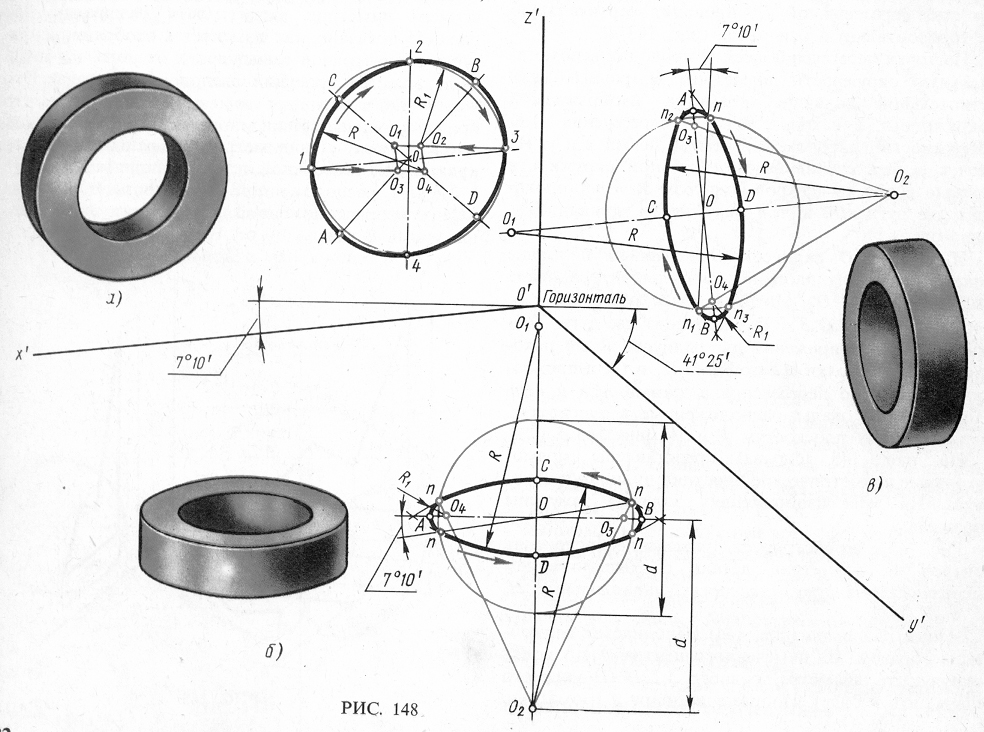Рассмотрим построение диметрической проекции окружности, лежащей в плоскостях П1 и П3 (рис.19,б,в). Через точку О проводим прямые параллельные осям x и y (в плоскости П1) и z и y ( в плоскости П3). Вверх и вниз (вправо и влево) от центра О откладываем отрезки, равные диаметру заданной окружности, получаем точки О1, О2. Приняв эти точки за центры, проводим (по направлению стрелок) радиусом R= О1n= О2n дуги овалов. Соединив точку О2 прямыми с концами дуги О2n на линии большой оси АВ, получаем точки О3, О4. Считая их центрами, проводим радиусом R1, замыкающие овал дуги.

Рис.19