Карты в цилиндрических проекциях
Цилиндрические проекции получаются путем проектирования поверхности глобуса на боковую поверхность цилиндра. В зависимости от положения оси цилиндра относительно оси вращения Земли цилиндрические проекции бывают нормальные, поперечные и косые. В РОСТО используются в основном карты, составленные в равноугольной поперечно-цилиндрической и косой равноугольной проекциях.
В равноугольной поперечно-цилиндрической проекции Гаусса составлены карты масштабов 1:500000 и крупнее.
Проекция Гаусса строится следующим образом. Вся поверхность Земли разделена на зоны меридианами, долготы которых кратны 6°. Каждая зона изображается на цилиндре, касающемся поверхности глобуса по среднему меридиану данной зоны (Рис. 7). Искажения длин пропорциональны расстоянию от среднего меридиана каждой зоны. Наибольшие искажения длин - на краю зоны (на экваторе) и равны 0,14%, т. е. 140 м на 100 км измеряемой длины. Такое изображение с малыми искажениями достигнуто за счет проектирования малых участков земной поверхности. Особенности проекции порождают разрывы между зонами, которые затрудни ют склейку листов карт соседних зон.
На картах крупного масштаба (1:200000 и крупнее) нанесены и оцифрованы вдоль рамок линии прямоугольных координат Х и V, составляющие километровую сетку прямоугольных координат Гаусса. Вертикальные километровые линии параллельны среднему меридиану данной зоны, принимаемому за ось X, а горизонтальные - экватору, принимаемому за ось У. Оцифровка горизонтальных линий (координата X) обозначает расстояние (в км.) от экватора до данной линии. Оцифровка вертикальных линий (координата У) дает номер зоны и расстояние от среднего меридиана зоны до данной линии, увеличенное на 500 км.
На карты 1:500000 километровая сетка не наносится, но, начиная с 1962 г. выносы, линий даются на рамках листов карт.
Прямоугольные координаты Гаусса применяются для определения положения геодезических пунктов и характерных ориентиров, используемых для привязки на местности объектов и различных радиотехнических устройств.
Угол g, заключенный между меридианом точки и вертикальной координатной линией, называется углом сближения меридианов (Рис. 8). Величина этого угла дается под южной рамкой крупномасштабной карты для средней точки листа или определяется по формуле:
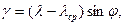
где j и l-координаты точки, в которой определяется угол;
lср. - долгота среднего меридиана данной зоны.
Направление a на ориентир С (см. Рис. 8), измеренное относительно вертикальной координатной линии, называется дирекционным углом.
Для определения истинного азимута А необходимо к измеренному дирекционному углу a алгебраически прибавить угол сближения меридианов 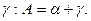
В косой равноугольной цилиндрической проекции издаются маршрутно-полетные карты масштабов 1:1000 000 и 1:2000000, предназначенные для обеспечения перелетов.
Эта проекция получается при проектировании земной поверхности на боковую поверхность цилиндра, расположенного под углом к оси вращения Земли.
Проекция строится в условных координатах. За условный экватор берется заданный большой, круг (ортодромия), по которому проходит ось маршрута. Полоса
вдоль оси маршрута переносится на боковую поверхность цилиндра, касающегося глобуса по этому большому кругу или секущего его по двум малым кругам.
В результате условный экватор (ортодромия) изображается прямой линией, условные параллели - прямыми, параллельными ортодромии, условные меридианы - равноотстоящими параллельными прямыми, перпендикулярными к ортодромии.
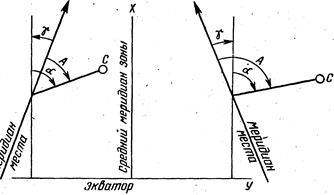
Рис. 8. Сближение меридианов g, дирекционный угол a и азимут А на картах в проекции Гаусса
По характеру искажений проекция равноугольна. Частные масштабы по главным направлениям равны. Если взять полосу маршрута шириной 10° дуги большого круга (по 5° в обе стороны от условного экватора), то максимальные искажения длин на краях карты составляют около 0,4%. В ряде случаев для уменьшения искажений на краях карты проектируют полосу маршрута на секущий цилиндр. Однако считают целесообразным с наименьшими искажениями длин изображать узкую полосу поверхности Земли, взятую вдоль ортодромического маршрута, так как по ней будет выполняться полет. Поэтому для создания маршрутно-полетных карт масштаба 1:1000000 круги сечения глобуса цилиндром берут отстоящими от условного экватора на 1° и на 2° - для карт масштаба 1:2000000. На этих картах относительные искажения длин вдоль осевых линий (условных экваторов) не превышают 0,02 и 0,06.
Рис. 9 Сборная разграфка.
Дата добавления: 2016-08-06; просмотров: 2852;











