Проверка устойчивости ветвей сквозной колонны.
Подкрановая ветвь. Гибкость в плоскости рамы
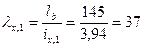 ,
,
где 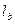 - расчетная длина ветви, равная расстоянию между узлами решетки (рис. 3. 5). Угол
- расчетная длина ветви, равная расстоянию между узлами решетки (рис. 3. 5). Угол 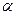 рекомендуется назначать
рекомендуется назначать 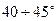 .
.
Примем для нашего примера 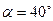 , тогда
, тогда
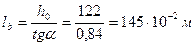 .
.
Коэффициент 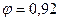 и напряжение
и напряжение
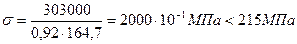 .
.
Из плоскости рамы:
гибкость 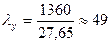 , коэффициент
, коэффициент 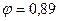 и напряжение
и напряжение
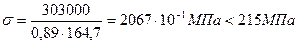 .
.
Недонапряжение 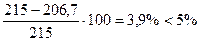 .
.
При недонапряжении более 5% пытаются подобрать сечение из меньшего профиля. В нашем случае оставляем двутавр № 70Б1.
Следует отметить, что в случае перенапряжения, полученного при проверке устойчивости ветви из плоскости рамы, следует уточнить расчетную длину ветви (например, путем установки прогона вдоль здания), что позволит снизить напряжение.
Обычно проверка устойчивости ветвей выполняется в предположении, что полученные для них максимальные сжимающие усилия действуют по всей длине.
В действительности они, ввиду переменного значения изгибающего момента по высоте колонны, также изменяются.
Так, для подкрановой ветви наибольшее сжимающее усилие 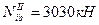 получено в сечении
получено в сечении 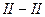 , где действует наибольший отрицательный изгибающий момент. По мере удаления от сечения
, где действует наибольший отрицательный изгибающий момент. По мере удаления от сечения 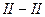 момент и одновременно усилие в подкрановой ветви уменьшается. Очевидно минимальное значение сжимающего усилия будет в сечении
момент и одновременно усилие в подкрановой ветви уменьшается. Очевидно минимальное значение сжимающего усилия будет в сечении 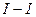 . Сначала в этом сечении необходимо определить
. Сначала в этом сечении необходимо определить 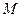 и
и 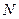 от тех же нагрузок, при которых определялись усилия в сечении
от тех же нагрузок, при которых определялись усилия в сечении 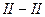 , т.е. нагрузок 1, 3 и 5, а затем и усилие
, т.е. нагрузок 1, 3 и 5, а затем и усилие 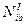 .
.
Изгибающий момент и продольная сила (с учетом собственного веса) в сечении 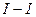 :
:
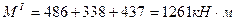 и
и 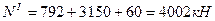 .
.
Усилие в подкрановой ветви в сечении 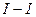 получим по формуле (3. 11)
получим по формуле (3. 11)
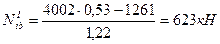 .
.
Знак при 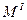 взят минус потому, что положительный момент в сечении
взят минус потому, что положительный момент в сечении 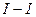 разгружает подкрановую ветвь.
разгружает подкрановую ветвь.
Для стержней с непостоянным сжимающим усилием СНиП [2, c. 18] рекомендует определять расчетную длину по формуле
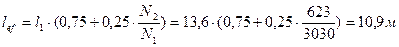 .
.
Теперь покажем, что даже при уточненной расчетной длине двутавр № 60Б2 не может быть принят для подкрановой ветви.
Гибкость 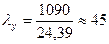 ;
; 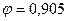 и напряжение
и напряжение
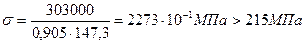
Наружная ветвь. Так как сечение наружной ветви состоит из нескольких профилей, сначала определим положение центра тяжести сечения. Статический момент относительно наружной грани (ось 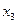 , рис. 3.1,в) равен
, рис. 3.1,в) равен 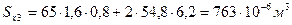 . Расстояние между осью
. Расстояние между осью 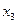 и осью
и осью 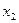
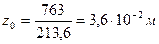 (предварительно было принято
(предварительно было принято 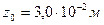 ).
).
Осевые моменты инерции:
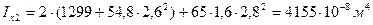
и
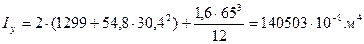 ;
;
Радиусы инерции:
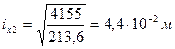
и
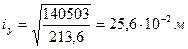 .
.
В плоскости рамы;
гибкость 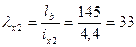 , коэффициент
, коэффициент 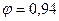 и напряжение
и напряжение
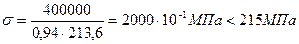 .
.
Из плоскости рамы
гибкость 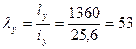 , коэффициент
, коэффициент 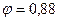 и напряжение
и напряжение
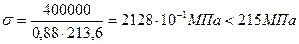
Расчёт раскосов соединительной решётки.Раскосы сквозной колонны рассчитывают на поперечную силу, равную большей из величин: фактической поперечной силе 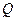 , полученной в результате статического расчета (табл. 2. 11) или условной
, полученной в результате статического расчета (табл. 2. 11) или условной 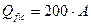 (в
(в 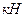 , для стали марки
, для стали марки 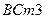 ) и
) и 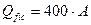 (для низколегированных сталей); здесь
(для низколегированных сталей); здесь 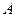 — суммарная площадь сечения ветвей стержня колонны. Усилие в раскосе при устройстве решетки в двух плоскостях:
— суммарная площадь сечения ветвей стержня колонны. Усилие в раскосе при устройстве решетки в двух плоскостях:
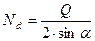 ,
,
где 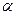 - угол между осью ветви и осью раскоса (рис. 3.5).
- угол между осью ветви и осью раскоса (рис. 3.5).
Двойка в знаменателе учитывает передачу поперечной силы на две плоскости решетки. Сечение раскосов принимается обычно из одного равнобокого уголка.
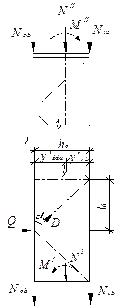 Рис. 3. 5. Схема решетки
сквозной колонны
Рис. 3. 5. Схема решетки
сквозной колонны
| Требуемую площадь сечения получим по формуле:
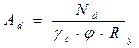 где
где 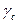 — коэффициент условий работы элементов решетки из одиночных уголков, прикрепляемых одной полкой (см. [3], табл. 9).
Стойки решетки рассчитываются на условную поперечную силу — коэффициент условий работы элементов решетки из одиночных уголков, прикрепляемых одной полкой (см. [3], табл. 9).
Стойки решетки рассчитываются на условную поперечную силу 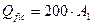 , где , где 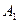 - площадь сечения более мощной ветви. Необходимо, чтобы гибкость раскосов и стоек не превышала 150. - площадь сечения более мощной ветви. Необходимо, чтобы гибкость раскосов и стоек не превышала 150.
|
Гибкость для одиночного уголка определяется по формуле:
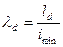 .
.
Устойчивость стержней решетки проверяется по формуле:
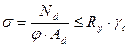 .
.
Как уже отмечалось, сквозные колоны, ширина нижней части которых менее 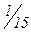 высоты
высоты 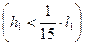 , должны проверяться на устойчивость как единый сжато – изогнутый стержень по формуле (3.3):
, должны проверяться на устойчивость как единый сжато – изогнутый стержень по формуле (3.3):
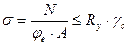
Проверку устойчивости следует производить дважды на расчетные усилия в сечении 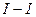 и в сечении
и в сечении 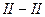 .
.
Коэффициент 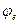 является функцией условной приведенной гибкости
является функцией условной приведенной гибкости 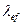 и относительного эксцентрицитета
и относительного эксцентрицитета 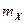 . Поскольку ветви стержня сквозной колонны соединены решеткой, приведенную гибкость относительно свободной оси
. Поскольку ветви стержня сквозной колонны соединены решеткой, приведенную гибкость относительно свободной оси 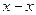 следует определять по формуле:
следует определять по формуле:
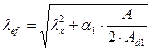 ,
,
где 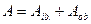 ;
;
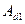 - площадь сечения одного раскоса (одного уголка);
- площадь сечения одного раскоса (одного уголка);
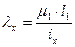 ;
;
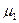 - коэффициент расчетной длины нижнего участка колонны;
- коэффициент расчетной длины нижнего участка колонны;
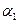 - коэффициент, определяемый по формуле
- коэффициент, определяемый по формуле 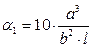 или по формуле:
или по формуле: 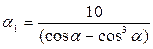 в зависимости от угла между ветвью и раскосом (рис. 3. 5).
в зависимости от угла между ветвью и раскосом (рис. 3. 5).
Относительный эксцентриситет получим по формуле:
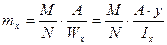 ,
,
где 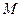 и
и 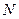 - расчетные усилия;
- расчетные усилия;
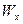 - момент сопротивления сечения относительно оси
- момент сопротивления сечения относительно оси  ;
;
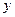 - расстояние между нейтральной осью сквозного сечения колонны и осью наиболее сжатой ветви, но не менее расстояния до оси стенки ветви; при проверке устойчивости на усилия в сечении
- расстояние между нейтральной осью сквозного сечения колонны и осью наиболее сжатой ветви, но не менее расстояния до оси стенки ветви; при проверке устойчивости на усилия в сечении 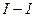 наиболее сжатой ветвью, как известно, будет наружная ветвь, для нее расстояние (до оси стенки
наиболее сжатой ветвью, как известно, будет наружная ветвь, для нее расстояние (до оси стенки 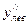 , см. рис. 6.1, в)
, см. рис. 6.1, в) 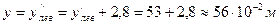 ; при проверке устойчивости на усилия из сечения
; при проверке устойчивости на усилия из сечения 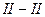 наиболее сжатой ветвью будет подкрановая и расстояние
наиболее сжатой ветвью будет подкрановая и расстояние 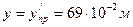 .
.
В случае если в результате проверки стержня сквозной колонны по формуле (3. 3) устойчивость его окажется не обеспеченной, следует площадь сечения одной или обеих ветвей увеличить. Удобнее при этом увеличивать толщину уголков наружной ветви колонны.
Дата добавления: 2017-09-01; просмотров: 2174;











