Усилия в стойках рамы от постоянных нагрузок
За лишние неизвестные при расчете рамы по методу деформаций принимаем углы поворота верхних узлов. Для симметричной однопролетной рамы углы поворота верхних узлов будут равны: 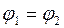 . Такая рама будет иметь лишь одно лишнее неизвестное
. Такая рама будет иметь лишь одно лишнее неизвестное 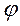 , которое получим из канонического уравнения:
, которое получим из канонического уравнения:
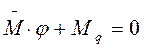 , (2.5)
, (2.5)
где 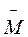 — сумма реактивных моментов в верхнем узле рамы при повороте его на угол
— сумма реактивных моментов в верхнем узле рамы при повороте его на угол 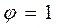 ;
;
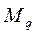 —сумма реактивных моментов в том же узле рамы от действия внешней нагрузки.
—сумма реактивных моментов в том же узле рамы от действия внешней нагрузки.
При шарнирном сопряжении ригеля со стойками расчет рамы сводится к расчету ступенчатых стоек. Для определения опорных давлений в верхних узлах стоек можно воспользоваться табл. 21 приложения.
Для решения уравнения (2.5) следует, прежде всего, определить усилия (изгибающие моменты) в элементах рамы от поворота верхних узлов на угол 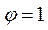 и построить эпюру моментов.
и построить эпюру моментов.
При повороте закреплений на угол 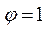 на концах ригеля рамы возникнут реактивные моменты:
на концах ригеля рамы возникнут реактивные моменты:
для П-образной рамы:
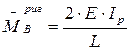 (2.6)
(2.6)
для Г-образной рамы:
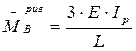 (2.7)
(2.7)
При повороте верхнего конца одноступенчатой стойки на угол 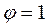 реактивные моменты на концах ее будут равны: в верхнем узле (сечение
реактивные моменты на концах ее будут равны: в верхнем узле (сечение  )
)
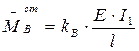 , (2.8)
, (2.8)
в нижней заделке (сечение 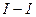 )
)
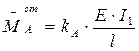 , (2.9)
, (2.9)
где 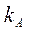 и
и 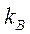 — абсолютные величины коэффициентов жесткости, получаемые по табл. 22,а приложения, в зависимости от параметров
— абсолютные величины коэффициентов жесткости, получаемые по табл. 22,а приложения, в зависимости от параметров 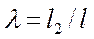 и
и 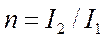 .
.
Реактивный момент в узле В при 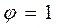 , очевидно, будет равен сумме:
, очевидно, будет равен сумме:
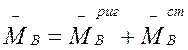 (2.10)
(2.10)
Реактивный момент в узле В от вертикальной равномерно распределенной нагрузки по ригелю будет равен:
для П-образной рамы 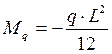 (2.11)
(2.11)
для Г-образной рамы 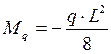 .
.
Угол поворота:
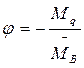 (2.12)
(2.12)
Теперь умножим полученные по формулам (2.6), (2.8) и (2.9) значения моментов на 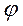 , просуммируем со значениями моментов в основной системе и построим эпюру изгибающих моментов в раме от постоянной нагрузки, приложенной к ригелю рамы.
, просуммируем со значениями моментов в основной системе и построим эпюру изгибающих моментов в раме от постоянной нагрузки, приложенной к ригелю рамы.
Пример 2. Определить значения изгибающих моментов, продольных и поперечных сил в стойках однопролетной симметричной рамы от равномерно распределенной нагрузки по ригелю 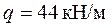 Пролет рамы
Пролет рамы 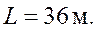 Стойки одноступенчатые
Стойки одноступенчатые 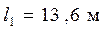 ,
,  и
и 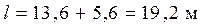 ; ширина верхней части стойки
; ширина верхней части стойки 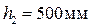 и нижней
и нижней 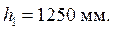
Установим относительные значения моментов инерции стоек и ригеля 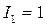 ;
; 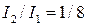 и
и 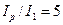 и определим параметры:
и определим параметры:
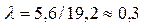 и
и 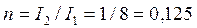 .
.
Реактивный момент в заделке ригеля при 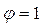 получим по формуле (2.6), выразив при этом
получим по формуле (2.6), выразив при этом 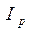 через
через 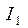 т. е.
т. е. 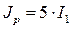 :
:
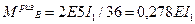
Примечание: жесткость 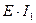 в дальнейшем при определении расчетных величин усилий сократится.
в дальнейшем при определении расчетных величин усилий сократится.
Абсолютные величины коэффициентов жесткости 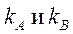 для определения реактивных моментов по формулам (2.8) и (2.9) получим из табл. 22, а приложения. Их следует определять с точностью не менее трех знаков после запятой и тщательно следить за правильностью расчетов. Вычисления произведем в табличной форме (табл. 2.3).
для определения реактивных моментов по формулам (2.8) и (2.9) получим из табл. 22, а приложения. Их следует определять с точностью не менее трех знаков после запятой и тщательно следить за правильностью расчетов. Вычисления произведем в табличной форме (табл. 2.3).
Таблица 2.3
Коэффициенты жесткости для 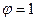
| Коэффициенты жесткости | 
| 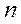
| ||
| 0,1 | 0,2 | 0, 125 | ||
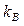
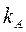
| 0,3 | - 0,58 | -1,055 | 0,699 |
| 0,3 | 0,687 | 0,887 | 0,737 |
Теперь по формуле (2.8) получим:
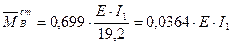
и по формуле (2.9):
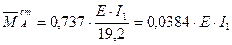 .
.
Реактивный момент в верхнем узле по формуле (2.10)
 .
.
Реактивный момент в том же узле от внешней нагрузки по формуле (2.11)
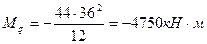 .
.
Угол поворота по формуле (2.12)
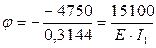
Сложим значения моментов от 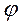 со значениями моментов в основной системе. Моменты в узле В получим:
со значениями моментов в основной системе. Моменты в узле В получим:
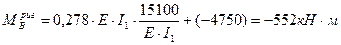
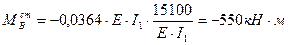
Примечание: при определении момента 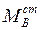 , реактивный момент, в соответствии с принятым для рамы правилом знаков, принят со знаком минус.
, реактивный момент, в соответствии с принятым для рамы правилом знаков, принят со знаком минус.
Момент в узле А (сечение 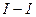 )
)
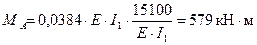
Несходимость (погрешность) в узле В составляет
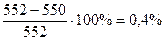
Момент в точке С (сечения 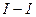 и
и 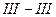 ) определится из подобия треугольников:
) определится из подобия треугольников:
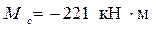
Изгибающие моменты в узлах В и А можно получить по готовым формулам:
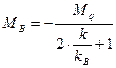 , (2.13) , (2.13)
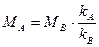 , (2.14)
где , (2.14)
где 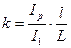 ; ;
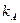 и и 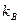 - коэффициенты жесткости стойки при повороте верхнего опорного сечения (узла - коэффициенты жесткости стойки при повороте верхнего опорного сечения (узла 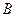 ) на угол ) на угол 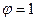 , принимаемые по табл. 22,а приложения, в формуле (2.13) со знаком плюс и в формуле (2.14) со своими знаками. , принимаемые по табл. 22,а приложения, в формуле (2.13) со знаком плюс и в формуле (2.14) со своими знаками.
|
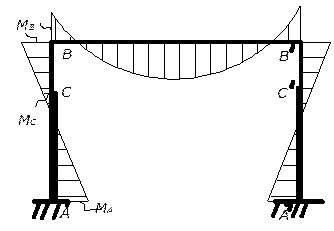 Рис. 2.6. Эпюра моментов в раме от вертикальных нагрузок, приложенных к ригелю.
Рис. 2.6. Эпюра моментов в раме от вертикальных нагрузок, приложенных к ригелю.
|
Формулами (2.13) и (2.14) рекомендуется пользоваться лишь в контрольных целях. В отдельных случаях, по указанию руководителя проекта, расчет рамы на вертикальные нагрузки, приложенные к ригелю, может быть выполнен только по формулам (2.13) и (2.14).
Эпюра моментов приведена на рис. 2.6.
При расчете многопролетной рамы на вертикальные нагрузки, приложенные к ригелю, как уже отмечалось ранее, расчленяют ее на простые П- и Г-образные рамы (рис. 2.2).
П-образные рамы рассчитывают по формулам (2.13) и (2.14). Момент в верхнем узле Г-образной рамы определяют по формуле
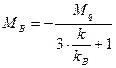 , (2.15)
, (2.15)
в нижнем узле — по формуле (2.14).
Обозначения для формулы (2.15) те же, что и для формулы (2.13). ступенчатых стойках рамы из-за смещения центров тяжести сечений верхней и нижней частей возникают изгибающие моменты. Величина момента равна произведению продольной силы верхней части стойки (опорных давлений стропильных и подстропильных ферм) на плечо, равное расстоянию между осями верхней и нижней частей стойки (рис. 2.7).
Эти моменты можно учитывать одновременно с расчетом рамы на вертикальные нагрузки, приложенные к ригелю, или рассматривать их как дополнительное загружение рамы.
Более целесообразным является второй способ, при котором отдельно определяют усилия (моменты) в элементах рамы от этого дополнительного загружения, а затем суммируют их с усилиями от нагрузки по ригелю. Это удобно еще и потому, что не всегда можно учесть дополнительное загружение рамы моментами одновременно с расчетом рамы на нагрузки по ригелю, как, например, при расчете рамы по формулам (2.13) и (2.15). В некоторых случаях, при малых значениях эксцентриситета между осями верхней и нижней частей стойки, дополнительными моментами можно пренебречь.
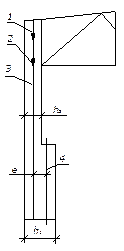
| Рис. 2.7. Загружение ступенчатой колонны нагрузкой от покрытия 1 – опорное давление подстропильных ферм; 2 – опорное давление ригеля рамы; 3 – ось верхней части колонны; 4 – ось нижней части колонны; |
Обе стойки загружены моментами по схеме, изображенной на рис. 2.8:
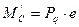 ,
где ,
где
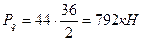 Плечо е впредположении, что центр тяжести сечения нижней части колонны проходит по середине ее ширины, будет равно:
Плечо е впредположении, что центр тяжести сечения нижней части колонны проходит по середине ее ширины, будет равно:
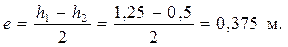 Тогда
Тогда 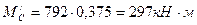
|
 Рис. 2.8. Эпюра моментов в раме от
Рис. 2.8. Эпюра моментов в раме от 
|
Момент 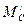 принимается приложенным на уровне подкрановой площадки колонны, обозначенной на схеме рамы буквой С (рис. 2.8). Таблица, с помощью которой будем определять коэффициенты жесткости (табл. 22, д приложения), позволяет получить значения усилий в стойках рамы при приложении момента в любой точке F по высоте
принимается приложенным на уровне подкрановой площадки колонны, обозначенной на схеме рамы буквой С (рис. 2.8). Таблица, с помощью которой будем определять коэффициенты жесткости (табл. 22, д приложения), позволяет получить значения усилий в стойках рамы при приложении момента в любой точке F по высоте 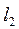 . При
. При 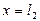 (см. рис. в заголовке табл. 22, д приложения) точка F совмещается с точкой С, в этом случае моменты в точке С будем обозначать
(см. рис. в заголовке табл. 22, д приложения) точка F совмещается с точкой С, в этом случае моменты в точке С будем обозначать 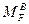 и
и 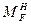 , ане
, ане 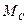 .
.
В табл. 22, д приложения значениякоэффициентов жесткости приведены для 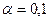 ;
; 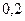 ;
; 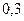 ;
; 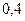 ; и
; и 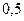 . Поэтому при промежуточных значениях
. Поэтому при промежуточных значениях 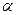 их следует вычислять по интерполяции между соседними страницами.
их следует вычислять по интерполяции между соседними страницами.
Коэффициенты жесткости получим из указанной выше таблицы по параметрам:
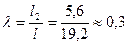 ;
;
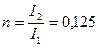 :
:
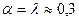 поскольку
поскольку  .
.
Значение коэффициентов жесткости определим по интерполяции (табл. 2.4).
Таблица 2.4
Коэффициенты жесткости для 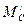
| Коэффициенты жесткости | 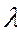
| 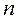
| ||
| 0,1 | 0,2 | 0,125 | ||
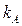
| 0,3 | −0,300 | −0,354 | −0,314 |
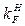
| 0,3 | 0,729 | 0,695 | 0,721 |
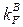
| 0,3 | −0,271 | −0,305 | −0,279 |
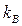
| 0,3 | 0,171 | 0,145 | 0,165 |
Знаки коэффициентов приняты обратные табличным, поскольку направление момента противоположно табличному.
Величины изгибающих моментов от действия 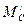 в характерных сечениях стоек определим по формулам, приведенным в табл. 22, д приложения.
в характерных сечениях стоек определим по формулам, приведенным в табл. 22, д приложения.
Сечение 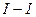
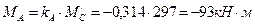

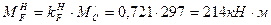
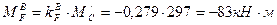
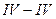
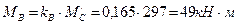
Эпюра моментов показана на рис. 2.8.
Просуммировав значения эпюр (рис. 2.6 и 2.8), получим расчетные величины изгибающих моментов от постоянной нагрузки по ригелю, по которым построим суммарную эпюру моментов (рис. 2.9).
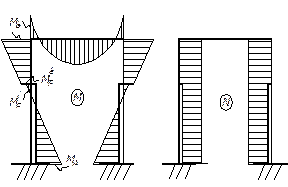 Рис. 2.9. Эпюра моментов и продольных сил от вертикальных нагрузок, приложенных к ригелю (с учетом момента
Рис. 2.9. Эпюра моментов и продольных сил от вертикальных нагрузок, приложенных к ригелю (с учетом момента 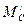 ) )
| Результаты расчетов рамы по каждому виду ее нагрузки рекомендуется сводить в таблицы, которые позволят легко произвести беглый проверочный расчет, как выполняющему, так и контролирующему расчет ( табл. 2.5). Продольная сила будет равна сумме опорных реакций ферм, опирающихся на верхнюю часть колонн (в том числе и подстропильных). |
Для нашего примера 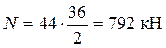 .
.
Эпюра продольных сил показана на рис. 2.9.
Правильность построения эпюры выполняется проверкой угла наклона 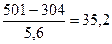 и
и 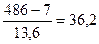 погрешность составит
погрешность составит 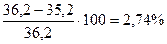 .
.
Поперечная сила в сечении 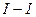
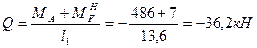 .
.
Таблица 2.5
Дата добавления: 2017-09-01; просмотров: 3133;











