Усилия в стойках рамы от крановых моментов
Крановые моменты принимаются приложенными на уровне подкрановых площадок в месте перехода нижней части колонны в верхнюю.
За лишнее неизвестное при расчете рамы методом деформаций принимается горизонтальное смещение верхних узлов рамы, которое может быть получено из канонического уравнения
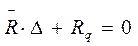 , (2.16)
, (2.16)
где 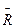 ÷ сумма реактивных усилий в фиктивном стержне при смещении ригеля на
÷ сумма реактивных усилий в фиктивном стержне при смещении ригеля на 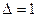 ;
;
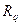 − сумма реактивных усилий в том же фиктивном стержне от заданных (внешних) нагрузок.
− сумма реактивных усилий в том же фиктивном стержне от заданных (внешних) нагрузок.
Для определения 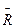 и
и 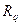 можно воспользоваться табл. 21 и 22 приложения.
можно воспользоваться табл. 21 и 22 приложения.
Порядок расчета следующий: с помощью таблиц определяют усилия в стойках рамы от единичного смещения верхних узлов рамы и усилия в стойках рамы основной системы, затем определяют смещение плоской рамы 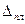 , коэффициент пространственной жесткости каркаса
, коэффициент пространственной жесткости каркаса 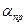 и смещение рамы в системе пространственного блока
и смещение рамы в системе пространственного блока 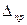 , потом, умножив значения моментов от
, потом, умножив значения моментов от 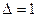 на
на 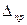 , получают усилия в стойках рамы от полного смещения рамы и, наконец, в результате суммирования - расчетные усилия.
, получают усилия в стойках рамы от полного смещения рамы и, наконец, в результате суммирования - расчетные усилия.
Ниже приведен пример расчета рамы на крановые моменты, который надлежит внимательно разобрать и усвоить, что облегчит решение последующих загружений рамы силами поперечного торможения кранов и ветровой нагрузкой, для которых числовые примеры не приводятся.
Пример 3. По данным примера 2 определим величины изгибающих моментов и продольных сил в стойках рамы от крановых моментов 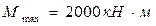 и
и 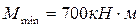 . Шаг рам 12 м, длина здания 120 м. Здание имеет продольный фонарь.
. Шаг рам 12 м, длина здания 120 м. Здание имеет продольный фонарь.
Коэффициенты жесткости для определения 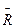 и изгибающих моментов от
и изгибающих моментов от  получим из табл. 22,6 приложения по параметрам
получим из табл. 22,6 приложения по параметрам 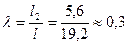 ; и
; и 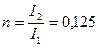 .
.
Таблица 2.6
Коэффициенты жесткости для 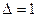
| Коэффициенты жесткости | 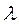
| 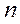
| ||
| 0,1 | 0,2 | 0,125 | ||
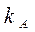
| 0,3 | −3,915 | −4,341 | −4,022 |
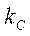
| 0,3 | −0,287 | 0,092 | −0,192 |
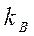
| 0,3 | 1,268 | 1,942 | 1,427 |
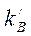
| 0,3 | −5,182 | −6,283 | −5,457 |
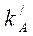
| 0,3 | 5,182 | 6,283 | 5,457 |
При определении коэффициентов жесткости особое внимание следует обратить на интерполяцию величин с разными знаками (например, для коэффициента 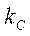 в табл.2.6), поскольку в этом случае легко можно сделать ошибку.
в табл.2.6), поскольку в этом случае легко можно сделать ошибку.
По формулам, приведенным в той же таблице, из которой получены коэффициенты жесткости, определим изгибающие моменты и реакции для стоек при смещении верхних узлов рамы на 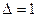 :
:
изгибающие моменты:
в сечении 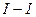
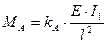 ;
;
в сечениях  и
и 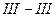
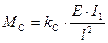
в сечении 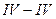
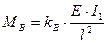
опорные реакции: в сечении 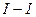
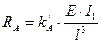
в сечении 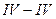
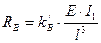
В последующих расчетах по определению усилий в стойках рамы Жесткость их 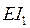 и высота
и высота 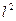 сократятся. Поэтому, в целях упрощения расчета примем обозначение
сократятся. Поэтому, в целях упрощения расчета примем обозначение 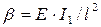 и подставим его, и значения коэффициентов жесткости табл. 2.6, в приведенные выше формулы. Таким образом, для одноступенчатой стойки рамы при взаимном смещении опор на
и подставим его, и значения коэффициентов жесткости табл. 2.6, в приведенные выше формулы. Таким образом, для одноступенчатой стойки рамы при взаимном смещении опор на 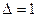 получим:
получим:
изгибающие моменты:
в сечении 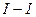
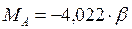 ;
;
в сечениях  и
и 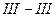
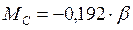 ;
;
в сечении 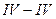
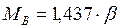 ;
;
опорные реакции в сечении 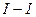
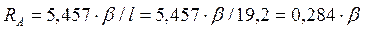 ;
;
в сечении 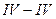
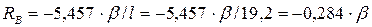
Реактивное усилие в фиктивном стержне при смещении верхних узлов рамы на 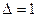 будет равно сумме абсолютных величин реакций
будет равно сумме абсолютных величин реакций 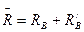 . В нашем случае для симметричной рамы
. В нашем случае для симметричной рамы
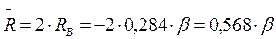 .
.
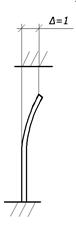
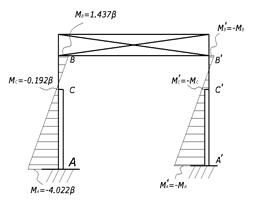
Эпюра изгибающих моментов в стойках при 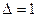 показана рис. 2.10.
показана рис. 2.10.
|
|
Коэффициенты жесткости для определения 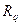 и изгибающих моментов в стойках при воздействии на раму крановыми моментами можно получить из табл. 22, д приложения. и изгибающих моментов в стойках при воздействии на раму крановыми моментами можно получить из табл. 22, д приложения.
|
Рис. 2.10 Эпюра моментов верхних узлов её на 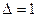
|
Они определяются в зависимости от 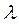 ,
, 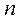 и
и 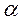 . В нашем случае
. В нашем случае 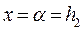 (рисунок и формулы табл.22,д приложения), следовательно,
(рисунок и формулы табл.22,д приложения), следовательно, 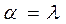 .
.
Коэффициенты жесткости 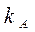 ,
, 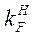 ,
, 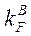 и
и 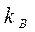 уже были вычислены для аналогичной нагрузки моментом
уже были вычислены для аналогичной нагрузки моментом 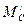 (табл. 2.4). Вписываем их в табл. 2.7 спротивоположными знаками, так как
(табл. 2.4). Вписываем их в табл. 2.7 спротивоположными знаками, так как 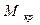 по направлению действия противоположен
по направлению действия противоположен 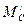 . Коэффициент для определения опорных реакций
. Коэффициент для определения опорных реакций 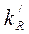 выписываем из табл. 22, д приложения.
выписываем из табл. 22, д приложения.
Часто параметры 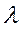 ,
, 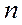 и
и 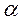 не совпадают с величинами, приведенными в табл. 22 приложения, и на вычисление коэффициентов жесткости затрачивается много времени. При этом, как показывает опыт, немало делается ошибок. В этом случае рекомендуем ограничиться определением коэффициентов
не совпадают с величинами, приведенными в табл. 22 приложения, и на вычисление коэффициентов жесткости затрачивается много времени. При этом, как показывает опыт, немало делается ошибок. В этом случае рекомендуем ограничиться определением коэффициентов 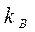 и
и 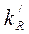 (или
(или 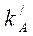 и
и 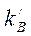 ) и с их помощью вычислить для сечения
) и с их помощью вычислить для сечения 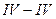
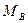 и
и 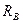 . В остальных сечениях изгибающие моменты определятся по правилам статики.
. В остальных сечениях изгибающие моменты определятся по правилам статики.
Таблица 2.7
Коэффициенты жесткости для 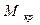
| Коэффициенты жесткости | 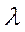
| 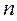
| ||
| 0,1 | 0,2 | 0,125 | ||
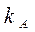
| 0,3 | 0,3 | 0,354 | 0,314 |
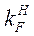
| 0,3 | −0,729 | −0,695 | −0,721 |
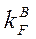
| 0,3 | 0,271 | 0,305 | 0,279 |
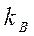
| 0,3 | −0,171 | −0,145 | −0,165 |
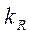
| 0,3 | 1,471 | 1,5 | 1,478 |
Изгибающие моменты и опорную реакцию внесем в табл. 2.8. Для правой стойки усилия вычисляем с помощью переходного коэффициента Mmin/Mmax=700/2000=0.35
Таблица 2.8
Дата добавления: 2017-09-01; просмотров: 1757;











