Закон Ома. Закон Джоуля-Ленца.

В предыдущем разделе рассмотрено физическое содержание понятий «электрический заряд» и «сила тока» («ток»), сформулирован закон сохранения электрического заряда и приведена математическая формулировка закона сохранения заряда в интегральной и дифференциальной формах. Следующий шаг в описании закономерностей физических явлений, связанных с наличием токов в материальной среде или в проводниках ограниченных геометрических размеров, состоит в установлении связи силы тока с такими характеристиками электрического поля как напряженность и разность потенциалов электрического поля. Трудности выявления упомянутых закономерностей в историческом аспекте связаны с тем, что получать искусственно значительные электрические заряды научились ещё в ХVIII веке, известный закон взаимодействия неподвижных точечных электрических зарядов был окончательно установлен Ш.О. Кулоном ещё в 1785 г., еще раньше были изобретены «лейденская банка» (конденсатор) и электроскоп. Проводить какие-либо опыты со стационарными токами стало возможно после изобретения А. Вольта в 1799 г. первого источника постоянного тока – «вольтова столба». Планомерные опыты с постоянными токами берут своё начало с экспериментов Г. Дэви 1821 года. Наибольшего успеха в этом направлении добился Г. Ом – закон Ома (открыт в 1826 г.) как основной закон теории электрических явлений сегодня изучают даже в школьном курсе физики.

Георг Ом выполнил большое количество экспериментов с постоянными токами и попытался свести известные и полученные им результаты в логически связную теорию. С этой целью он принял идею о сравнении потока электрического заряда вдоль проводника с потоком теплоты вдоль проволоки, теория теплопроводности была разработана Ж.Б.Ж. Фурье в 1822 году и опубликована в монографии «Аналитическая теория теплоты». «Я начал – говорит Г. Ом, - с предположения, что передача электричества от одной частицы происходит только к соседней с ней, так что немедленный переход электричества от этой частицы к любой другой, расположенной дальше, невозможен. Я принял, что поток между двумя соседними частицами, при прочих абсолютно одинаковых условиях, пропорционален разности электрических сил, существующих в двух частицах; также как в теории тепла поток теплоты между двумя частицами считается пропорциональным разности их температур».

В идее Г. Ома следует уточнить, какая физическая величина играет роль, аналогичную температуре в теории теплопроводности. А. Вольта характеризовал «вольтов столб» электроскопической силой, мерой величины которой служила величина расхождения листочков электроскопа, соединенного с одним из концов вольтова столба, в то время как второй конец вольтова столба был заземлен. Г. Ом принял, что электрическая сила в его теории – это сила электроскопическая. Современное понятие рассматриваемой «силы» связано с догадкой Г. Кирхгофа: электроскопичесая сила – это потенциал электростатического поля (1849 год). Легко видеть, что выработка научных представлений – весьма непростое дело.

Итак, вспомним первый закон Фурье для изотропной теплопроводной среды:

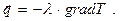(1)

Здесь 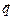- вектор плотности потока тепла (величина, модуль которой равен количеству тепла, переносимому через поверхность единичной площади за единицу времени, если площадка ориентирована перпендикулярно векторным линиям поля 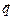), 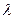- коэффициент теплопроводности, 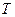- температура среды. Используем физическую аналогию, предложенную Г. Омом для изотропной электропроводной среды, с учетом поправки Г. Кирхгофа (рис. 1):

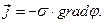(2)

Здесь 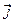- объёмная плотность тока, 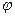- потенциал электростатического поля, 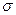- электропроводность среды (обратная величина удельному электрическому сопротивлению).

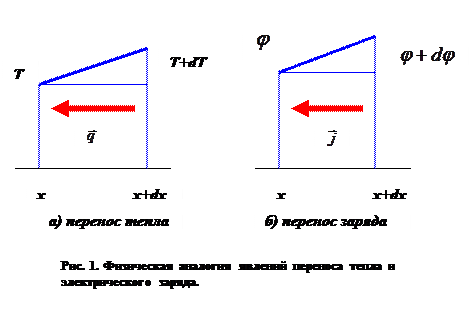
В электростатике известно соотношение:

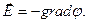(3)

Здесь 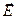- напряженность электрического поля. С учетом соотношения (3) перепишем уравнение (2) в форме:

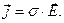(4)

Зависимость (4) является дифференциальной формой закона Ома для электропроводящей среды в отсутствие сторонних сил, действующих на носители электрического заряда.

Рассмотрим тонкий проводник постоянного поперечного сечения 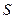. Предположим, что вектор объёмной плотности тока направлен вдоль проводника и сохраняет постоянное значение в каждой точке поперечного сечения проводника. Предположим, что вектор напряженности электрического поля 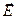и электропроводность среды постоянны в каждой точке объёма проводника. В этом случае можно записать следующую последовательность соотношений:

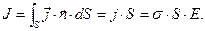(5)

Если ввести понятие «падение напряжения» 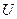соотношением

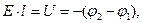(6)

а сопротивление проводника 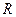определить с помощью формулы

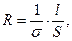(7)

то итоговое из соотношений (5) приобретает канонический вид:

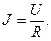(8)

Зависимость (8) является интегральной формой закона Ома для простейшего участка цепи.

Если у однородного проводника площадь поперечного сечения зависит от продольной координаты, соотношение (8) можно переписать в форме зависимости между дифференциалами соответствующих величин:

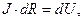
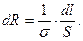(9)

Значение силы тока вдоль проводника сохраняется, если проводник не имеет разветвлений. Это соображение позволяет определить сопротивление однородного проводника переменного сечения:

(10)

где в качестве пределов интегрирования следует понимать положение крайних поперечных сечений проводника.

Закон Ома в дифференциальной форме (4) в сочетании с законом сохранения электрического заряда в дифференциальной форме

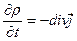(11)

для однородной изотропной среды ( 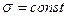) приводит к соотношению:

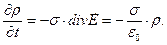(12)

Уравнение (12) описывает «релаксацию» объёмной плотности электрического заряда:

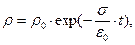(13)

здесь 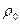- объёмная плотность электрического заряда в точке наблюдения в начальный момент времени. Из зависимости (13) следует, что объёмная плотность электрического заряда в однородной изотропной проводящей среде с течением времени экспоненциально стремится к нулю. Заметим, что из этого результата не следует, что объёмная плотность тока 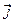в проводящей среде обращается в нуль. Дело в том, что в реальных средах имеются носители электрического заряда разного знака и разной подвижности. В соотношении (13) содержится суммарная объёмная плотность электрического заряда. Стремление этой величины к нулю означает, что в проводящей среде с течением времени должно достигаться состояние электронейтральности. Отмеченное свойство электропроводящей среды (и проводника в целом) играет важную роль в проявлении силового взаимодействия проводников, по которым текут токи. Это взаимодействие не является кулоновским.

Рассмотрим случай, когда в электропроводящей среде помимо напряженности электростатического поля имеется напряженность сторонних сил, действующих на носители электрического заряда. Естественным обобщением закона Ома в форме (4) является зависимость:

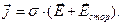(14)

Зависимость (14) ниже рассматривается как теоретическое обобщение экспериментальных результатов. С помощью рассуждений, подобных использованным при выводе интегральной формы закона Ома (8) для простейшего участка электрической цепи, легко получить обобщенный закон Ома для участка цепи в интегральной форме:

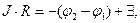(15)

где символом 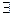обозначена электродвижущая сила источника тока, находящегося на рассматриваемом участке электрической цепи.

Если рассматриваемый участок цепи является замкнутым (простейшая электрическая схема), то потенциал конца участка 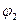совпадает с потенциалом начала участка 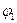, при этом соотношение (15) приобретает вид

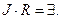(16)

В механике из основного закона динамики материальной точки скалярным умножением обеих частей уравнения на скорость материальной точки получают закон сохранения механической энергии, если движение происходит под действием консервативных сил. В теории электрических токов скорость перемещения носителей заряда связана с величиной тока. Умножим обе части уравнения (16) на величину тока :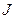

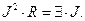(17)

В левой части уравнения (17) содержится мощность выделения джоулева тепла (закон Джоуля-Ленца, открытый в 1841 г.), в правой части – мощность источника тока. Уравнение (17) представляет собой формулировку закона сохранения энергии: в простейшем замкнутом контуре мощность источника тока равна мощности выделения тепла при прохождении тока через сопротивление.