Электрический ток и закон сохранения электрического заряда.

Понятие «электрический ток» неразрывно связано с понятием «электрический заряд». В начале ХIX века считалось, что существует так называемая электрическая жидкость, которая наполняет собой физические тела и обладает свойством перетекать от одного тела к другому. Избыток в теле «положительной электрической жидкости» интерпретировался как положительный электрический заряд тела, избыток «отрицательной электрической жидкости» или недостаток «положительной электрической жидкости» интерпретировался как отрицательный электрический заряд тела. Течение электрической жидкости по проводнику конечного поперечного сечения можно уподобить течению обычной жидкости, например, воды по трубопроводу. Поток массы вещества вдоль трубопровода порождает представление о потоке электрического заряда вдоль проводника конечного поперечного сечения. В первом случае фундаментальным законом является закон сохранения массы вещества, во втором случае – открытый в 1750 г. Б. Франклином закон сохранения электрического заряда: электрический заряд не может возникнуть или исчезнуть, он может только полностью или частично переместиться в пространстве, т.е. перейти с одного тела на другое.

Поток 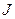электрического заряда называют «силой тока» или просто «током» и вводят соотношением:

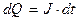, (1)

где 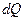- положительный электрический заряд, прошедший контрольное сечение проводника за время 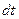(условно принято считать, что положительное направление тока связано с движением положительного электрического заряда). Элементарный поток электрического заряда 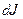связан с вектором объёмной плотности тока выражением:

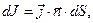(2)

где 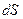- элемент контрольной поверхности, 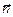- единичный вектор нормали к элементу контрольной поверхности 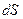, 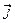- объёмная плотность потока электрического заряда.

Последняя величина имеет специальное название: объёмная плотность тока. Заметим, что объёмная плотность тока является векторной величиной.

После интегрирования соотношения (2) по контрольной поверхности 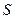получаем:

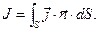(3)

Соотношением (3) сила тока определена как поток вектора объёмной плотности тока через контрольную поверхность 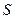. Определение потока вектора через поверхность и обсуждение физического содержания этого понятия было проведено в разделе электростатика. Здесь только напомним, что сила тока является скалярной (алгебраической) величиной: подынтегральная функция в соотношении (3) является скалярной функцией.

Если рассмотреть некоторое электрически заряженное физическое тело и окружить его замкнутой поверхностью 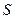, то с помощью определений (1) и (3) получим математическое выражение закона сохранения электрического заряда:

. (4)

Знак «минус» в правой части закона сохранения (4) электрического заряда связан с тем, что при вычислении потока электрического заряда через замкнутую контрольную поверхность принято использовать внешнюю (!) по отношению к контрольному объёму нормаль 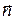. Электрический заряд в рассматриваемой системе может измениться с течением времени только при условии, что суммарный поток электрического заряда (т.е. электрический ток) через замкнутую контрольную поверхность отличен от нуля. Электрический заряд внутри замкнутой контрольной поверхности остаётся неизменным, если втекающий поток электрического заряда 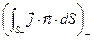равен вытекающему потоку электрического заряда 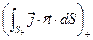, т.е. ток, поступающий в контрольный объём, равен току, уходящему из контрольного объёма.

Закон сохранения (4) электрического заряда записан в интегральной форме, т.е. в целом для контрольного объёма, ограниченного замкнутой контрольной поверхностью. Если конфигурация контрольного объёма с течением времени остаётся неизменной, если электрический заряд элемента контрольного объёма можно описать с помощью объёмной плотности электрического заряда

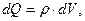(5)

то уравнение (4) можно переписать в форме:

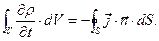(6)

С использованием теоремы Остроградского-Гаусса правую часть уравнения (6) можно преобразовать в интеграл по контрольному объёму :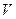

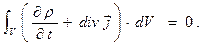(7)

Уравнение (7) должно выполняться для произвольного объёма 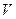, поэтому единственной возможностью обращения в нуль левой части уравнения (7) является обращение в нуль подынтегральной функции в любой точке внутри контрольного объёма, практически в любой точке пространства. Обычно записывают полученный результат в так называемой «дивергентной» форме:

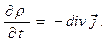(8)

Уравнение (8) является дифференциальным уравнением в частных производных, оно описывает локальное изменение объёмной плотности электрического заряда с течением времени (левая часть уравнения(8)), связывая скорость этого изменения с величиной дивергенции («расходимости») векторного поля объёмной плотности тока (правая часть уравнения (8)). Если объёмную плотность тока 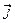представить в форме

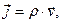(9)

где 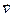- макроскопическая скорость переноса электрического заряда (физическое содержание соотношения (9) подробно обсуждается в разделе «Материальные уравнения среды»), уравнение (8) приобретает вид:

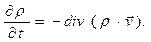(10)

Заметим, что локальные законы сохранения в физике (закон сохранения массы вещества, закон сохранения энергии и т.п.) записываются в форме (10). Говорят, что форма записи закона сохранения (10) имеет фундаментальный характер. Левая часть закона сохранения представляет собой частную производную от объёмной плотности рассматриваемой величины, а правая часть – взятую со знаком минус дивергенцию векторного поля объёмной плотности потока рассматриваемой величины.

На поверхности раздела двух проводящих сред с разными физическими свойствами закон сохранения электрического заряда принимает специфическую форму:

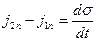. (11)

Здесь 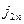и 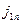- нормальные к поверхности раздела компоненты векторов объёмной плотности тока проводимости (касательные компоненты не привносят электрический заряд на поверхность раздела), 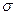- поверхностная плотность стороннего электрического заряда. Вывод условия (11) практически полностью совпадает с выводом соотношений на границе раздела двух диэлектриков нормальных компонент вектора электрической индукции (раздел 4.6). Заметим, что приведённая форма записи закона сохранения стороннего электрического заряда (11) справедлива в отсутствие поверхностного растекания электрического заряда (отсутствие поверхностных токов проводимости).

В заключение настоящего раздела обратим внимание читателя на то обстоятельство, что дифференциалы электрического заряда 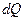в выражении (1) и в выражении (5) имеют различающийся физический смысл. В первом случае речь идёт о величине заряда, прошедшего за время 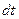контрольную поверхность. Эту величину можно связать с суммарным электрическим зарядом контрольного объёма в целом уравнением баланса. Во втором случае речь идет о величине электрического заряда, который содержится в элементе контрольного объёма 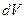в рассматриваемый момент времени. Если в первом случае речь идёт о «процессе», то во втором случае – о «состоянии». Невнимательность при использовании определений (1) и (5) может привести к ошибочным результатам.