Погонная ёмкость двухпроводной линии.

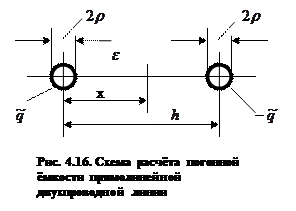
Рассмотрим два прямолинейных бесконечно протяженных тонких параллельных друг другу проводника с расстоянием h между ними. Пусть поперечные сечения проводников представляют собой круги радиусом 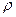. Пусть первый проводник заряжен постоянной погонной плотностью положительного заряда 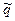, а второй проводник – такой же плотностью отрицательного заряда. Пусть безграничное пространство, в котором расположены проводники, заполнено однородной средой с известной величиной диэлектрической проницаемости 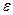(рис. 1).

Строгое рассмотрение задачи требует определения поверхностной плотности электрических зарядов в зависимости от положения точки наблюдения на контуре поперечного сечения для обеспечения постоянных значений электрических потенциалов на боковых поверхностях проводников. Такое решение задачи существует, оно получается с помощьюиспользования бицилиндрических координат и приводит к замкнутому аналитическому решению. Здесь мы используем предположение о том, что радиус поперечного сечения проводников значительно меньше расстояния между ними, это позволяет считать распределение зарядов по поверхности проводников равномерным. Сравнение с точным решением позволяет проверить корректность принятого предположения.

В силу принципа суперпозиции результирующее поле вектора 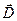складывается из поля, образованного электрическим зарядом на левом проводе линии, и из поля, образованного зарядом на правом проводе. Для того и другого поля с помощью интегральной формы теоремы Гаусса для вектора 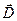в случае осевой симметрии получаем с учётом знаков равномерно распределённых по длине электрических зарядов:

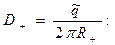
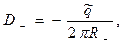(1)

где R₊ и R_- представляют собой радиусы контрольных цилиндрических поверхностей, соосных с рассматриваемыми проводниками. Выражения (1) позволяют выписать суммарное значение напряженности электрического поля вдоль линии, соединяющей оси проводников (поперечная координата задачи):

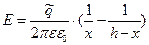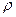, <x<(h- 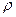), (2)

и вычислить разность потенциалов между боковыми поверхностями проводников

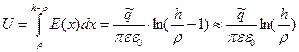. (3)

В соответствии с определением емкости вычислим погонную ёмкость 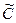рассматриваемой системы проводников:

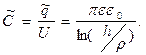(4)

Частный случай ( 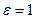) зависимости (4) понадобится нам в последующем при анализе квазистационарных процессов в двухпроводной линии.