Цилиндрический конденсатор с неоднородным диэлектриком.

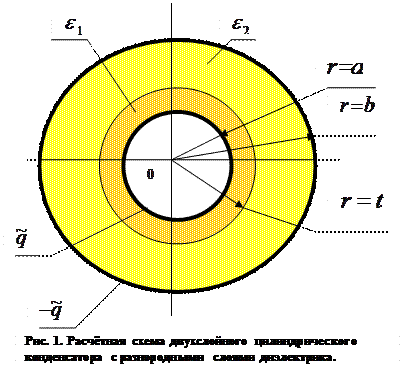
Рассмотрим конструкцию конденсатора, который образован двумя проводящими коаксиальными круговыми цилиндрическими поверхностями, протяженность которых вдоль продольной оси значительно превосходит величину зазора между ними (приближение конденсатора бесконечной длины, возможность не учитывать краевые эффекты). Пусть радиус поперечного сечения внутренней поверхности равен 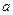, радиус поперечного сечения наружной поверхности равен 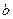, погонная плотность электрического заряда на внутренней поверхности равна постоянной величине 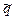, постоянная погонная плотность электрического заряда на внешней поверхности равна 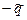(заряды равны по величине и отличаются друг от друга только знаком, физическая размерность этих величин - 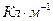). Поверхностные плотности электрических зарядов на обкладках конденсатора имеют значения

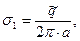
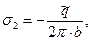(1)

при записи выражений (1) предполагается, что электрические заряды распределены по поверхности обкладок конденсатора равномерно по периметру поперечного сечения. Внутреннее пространство конденсатора заполнено диэлектриком, причем однородный цилиндрический слой а < r < t имеет относительную диэлектрическую проницаемость 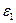, а

однородный цилиндрический слой t < r < b имеет относительную диэлектрическую проницаемость 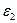. Среда 1 и среда 2 являются изотропными средами.

Несколькими способами можно доказать, что равномерно заряженная проводящая цилиндрическая поверхность не создаёт электрического поля во внутреннем объёме полости.

Действительно, в этой области источники поля 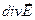и 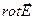равны нулю, потенциал на границе области имеет постоянное значение. Из курса математики известно, что если потенциал внутри области сохраняет постоянное значение, градиент этой величины равен нулю, значит, вектор 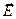и вектор 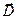обращаются в нуль.

Внешность конденсатора тоже обладает этим свойством. Действительно, рассмотрим произвольную точку в плоскости, перпендикулярной оси симметрии конденсатора, во внешнем по отношению к конденсатору пространстве. Пусть через эту точку проходит окружность с центром на оси симметрии. Вектор 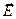в рассматриваемой точке можно разложить на нормальную к окружности и касательную к окружности компоненты. Для касательной компоненты имеем условие потенциальности электрического поля

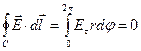, (2)

где 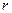- постоянный радиус рассматриваемой окружности. Из соображений симметрии величина 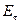должна быть одинакова для всех точек рассматриваемой окружности, поэтому из соотношения (2) следует, что 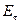обращается в нуль. Из интегральной формы теоремы Гаусса (контрольный объём выбран единичной длины вдоль осевой координаты) следует

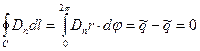. (3)

Соотношение (3) справедливо, поскольку компонента вектора 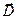вдоль оси симметрии конденсатора, очевидно, равна нулю, а поток вектора 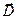через контрольную замкнутую поверхность единичной длины вдоль оси симметрии определяется левой частью соотношения (3). Из условия симметрии следует, что нормальная компонента вектора 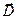на рассматриваемой окружности должна иметь постоянное значение и в силу соотношения (3) обратиться в нуль.

Для расчёта электрического поля в зазоре между обкладками конденсатора используем интегральную форму теоремы Гаусса (контрольный объём выбран единичной длины вдоль осевой координаты):

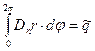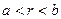, . (4)

Обоснование соотношения (4) можно выполнить по аналогии с обоснованием результата (3). Из уравнения (4) следует

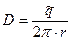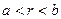, . (5)

Теперь несложно рассчитать следующие зависимости:

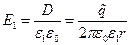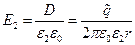, , (6)

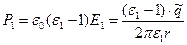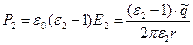, (8)

в соответствующих интервалах изменения независимой переменной.

Зависимости (6) позволяют рассчитать падение напряжения на обкладках конденсатора:

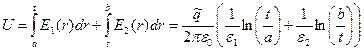. (9)

Выражение (9) позволяет рассчитать погонную ёмкость рассматриваемого цилиндрического конденсатора (т.е. ёмкость, рассчитываемую на единицу длины конденсатора без учета краевых эффектов):

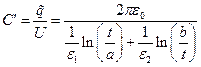. (10)

Физическая размерность погонной ёмкости цилиндрического конденсатора совпадает с размерностью электрической постоянной - 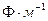. Формула (10) описывает рассматриваемый двухслойный конденсатор как последовательное соединение двух однослойных конденсаторов.

Использование условий на поверхностях разрыва электрических свойств среды для первой и второй обкладок конденсатора и для границы раздела диэлектрических слоёв приводит к результату:

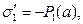
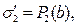
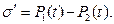(11)

Заметим, что в рассматриваемом случае вектор 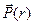поляризованности среды имеет единственную радиальную компоненту, а радиальное направление совпадает с направлением нормали к цилиндрической поверхности.

В цилиндрическом конденсаторе не возникает объёмная плотность связанных зарядов:

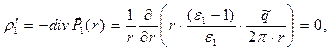
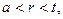(12)

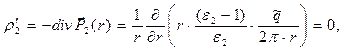
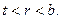(13)

При вычислении выражений (12) и (13) использована запись дивергенции вектора в цилиндрической системе координат и учтено, что рассматриваемые векторы имеют только радиальную компоненту.

Сумма связанных электрических зарядов в пересчёте на единицу длины вдоль осевой координаты для рассматриваемого конденсатора равна нулю:

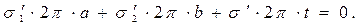(14)

В заключение приведём выражение для погонной ёмкости протяженного цилиндрического конденсатора с однородным диэлектриком

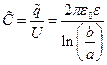. (15)

Если учесть, что 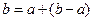и рассмотреть случай малого зазора 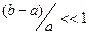, то, раскладывая логарифм в знаменателе формулы (15) в ряд Тэйлора в окрестности единицы с точностью до членов второго порядка малости, получим приближенное выражение

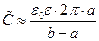. (16)

Легко видеть, что выражение (16) после умножения обеих частей формулы (16) на «длину конденсатора» совпадает с формулой для ёмкости плоского конденсатора с однородным диэлектриком.