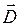Плоский конденсатор с неоднородным диэлектриком.

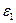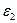Рассмотрим плоский конденсатор, образованный двумя параллельными пластинами достаточно больших размеров в плане по сравнению с величиной зазора между ними. Пусть пространство между пластинами заполнено двумя однородными изотропными диэлектрическими слоями с относительными диэлектрическими проницаемостями и , причем граница раздела этих слоёв является плоскостью, параллельной пластинам конденсатора. Пусть поперечная координата первой пластины конденсатора равна нулю, поверхность раздела диэлектриков описывается координатой 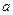, а вторая пластина – координатой 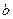. Допустим, что на первой пластине конденсатора сосредоточен положительный электрический заряд с поверхностной плотностью 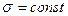, а на второй пластине – такой же отрицательный заряд. Электрическое поле в конденсаторе (и в окружающем пространстве) определяется совокупностью свободных электрических зарядов на обкладках конденсатора и связанными электрическими зарядами в неоднородном диэлектрике.

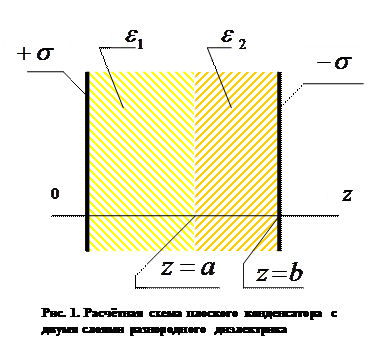Напряженность 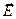электрического поля, образованного поверхностными зарядами первой пластины (считаем, что её размеры бесконечны), направлена перпендикулярно пластине конденсатора. Действительно, опустим из произвольной точки наблюдения перпендикуляр на плоскость первой обкладки и рассмотрим произвольный элементарный заряд пластины 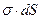с координатами (x,y) относительно основания перпендикуляра. Очевидно, что каждому такому элементарному заряду найдется аналогичный по величине заряд с координатами (-x,-y) . Совокупность рассмотренных зарядов не создаёт проекции вектора 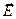на касательное направление к первой обкладке конденсатора. Из соображений симметрии заключаем, что нормальные проекции вектора 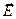для точек наблюдения, симметричных относительно первой пластины, равны по величине и направлены в противоположные стороны. Поскольку вектор 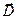пропорционален вектору 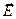и его расчёт не требует непосредственного учёта влияния связанных электрических зарядов, можно утверждать, что компоненты вектора 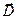обладают отмеченными свойствами компонент вектора 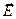. В этом случае для расчёта величины вектора 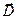можно использовать интегральную форму теоремы Гаусса, контрольный объём удобно выбрать в форме цилиндра с образующей, перпендикулярной плоскости первой обкладки, и поперечными сечениями, параллельными указанной плоскости. Пусть поперечные сечения цилиндра равноудалены от обкладки конденсатора. Теорема Гаусса для вектора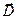

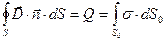(1)

принимает вид

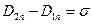, (2)

где нормаль к поверхности обкладки конденсатора направлена вдоль поперечной координаты. На рисунке 2 приведена расчётная схема определения поля вектора 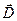около

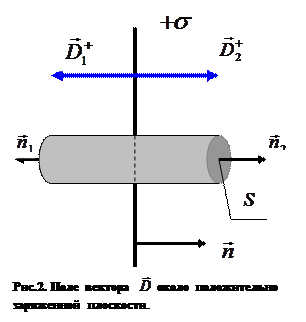
положительно заряженной плоскости. В рассматриваемом случае 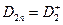, , 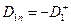напомним, что векторы 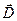справа и слева от заряженной плоскости проектируются на одну и ту же нормаль 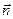. В силу симметрии распределения электрического заряда имеет место равенство: 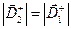, из которого следует соотношение

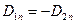. (3)

С учётом полученного соотношения (3) из условия (2) получим

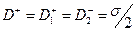. (4)

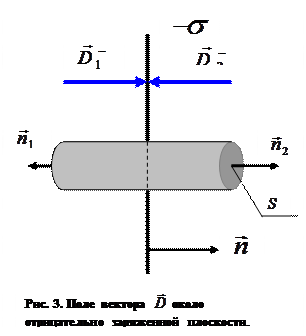
Рассмотрим расчётную схему определения вектора 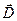в окрестности отрицательно заряженной плоскости (рис.3). . В рассматриваемом случае 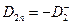, 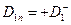. Из условия симметрии задачи следует утверждение 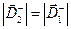. В рассматриваемой схеме справедливо соотношение (3), с учётом которого из условия (2) получаем:

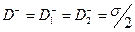. (5)

В классической электродинамике (линейное приближение) справедлив принцип суперпозиции. Рассматривая рисунок 4, приходим к выводу, что вектор 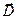вне конденсатора обращается в нуль, а в пространстве между пластинами имеет место соотношение:

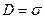. (6)

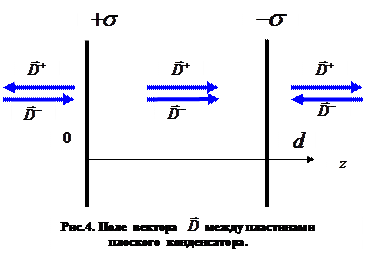
Вычисленный вектор 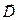направлен в сторону возрастания поперечной координаты.

Заметим, что соотношение (6) можно было бы получить непосредственно, рассматривая условие (2) для левой (или правой) обкладки конденсатора с учётом обращения в нуль поля вектора 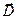вне конденсатора. Если нормаль к левой обкладке конденсатора направлена вдоль координаты 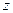, имеем 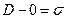. Если рассмотреть правую обкладку конденсатора и нормаль направить вдоль координаты 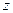(во внешнее пространство), получим 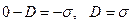. При этом было необходимо сделать предположение о том, что поле вектора 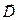в пространстве между обкладками является однородным.

Теперь легко рассчитать величины напряжённостей электрического поля в первом диэлектрическом слое конденсатора и во втором

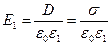, 0<x<a, 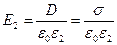, a<x<b. (7)

Далее вычисляем величину падения напряжения между обкладками конденсатора

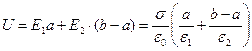. (8)

В соответствии с определением понятия «ёмкость конденсатора» вычисляем ёмкость конденсатора с площадью пластин, равной величине 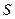, без учёта краевых эффектов (т.е. без учета искажения однородного поля вблизи краёв конденсатора):

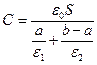. (9)

Легко видеть, что из полученного выражения следует соотношение:

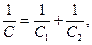
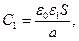
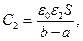(10)

характерное для последовательного соединения конденсаторов с однородным диэлектриком.

Для величин поляризованности среды справедливы зависимости

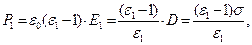
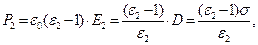(11)

последнее позволяет вычислить величину поверхностной плотности связанного электрического заряда на границе раздела диэлектрических слоёв:

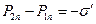. (12)

Величины 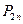и 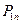вычисляются как предельные справа и слева от плоскости, координата которой равна a. Расчётная схема на рис. 5 поясняет содержание условия (12) и позволяет получить итоговую зависимость

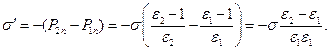
(13)

Из зависимости (13) следует, что поверхностная плотность связанного электрического заряда обращается в нуль на границе раздела двух сред, если диэлектрические свойства слоёв 1 и 2 одинаковы. Теорема Гаусса для вектора поляризации среды позволяет вычислить поверхностную плотность связанного электрического заряда и на обкладках конденсатора:

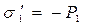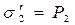, . (14)

Легко видеть, что поляризация диэлектриков приводит к уменьшению абсолютной величины суммарного заряда на обкладках конденсатора. Интересно отметить, что сумма связанных электрических зарядов в конденсаторе равна нулю:

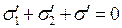. (15)

Объёмная плотность 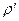связанных электрических зарядов определяется дивергенцией вектора поляризации среды. В рассматриваемом случае и в первом, и во втором слое вектор поляризации является постоянным, что приводит к обращению в нуль объёмной плотности связанных зарядов.

В заключение заметим, что при решении задачи о расчёте характеристик электростатического поля в плоском конденсаторе можно было бы воспользоваться и дифференциальной формой теоремы Гаусса

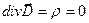. (16)

Здесь 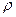- объёмная плотность свободных электрических зарядов. Из соображений симметрии очевидно, что вектор 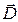может иметь только поперечную компоненту и её величина может зависеть только от поперечной координаты. Из уравнения (15) в рассматриваемом случае

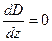(17)

получается, что величина 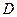является константой, значение которой устанавливается из соотношений для нормальных компонент вектора 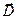на первой или на второй обкладке конденсатора. Заметим, что в рассматриваемом случае важно, чтобы поверхностная плотность свободных электрических зарядов на обкладках конденсатора была одинаковой по величине и разной по знаку заряда. Это условие обеспечивает обращение в нуль вектора 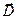во внешнем пространстве конденсатора.