Сферический конденсатор с однородным диэлектриком.

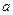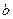Пусть конденсатор состоит из двух концентрических сферических проводящих поверхностей радиусов и , (b > a), пространство между которыми заполнено однородным диэлектриком с относительной диэлектрической проницаемостью 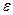. Пусть на внутренней поверхности имеется положительный электрический заряд Q, равномерно распределённый по поверхности сферы. Пусть на внешней поверхности имеется такой же по величине электрический заряд противоположного знака, тоже равномерно распределённый по поверхности сферы (рис. 1).

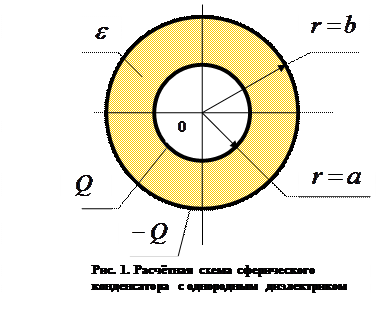Указанные предположения обуславливают отсутствие электрического поля внутри первой сферы и вне второй сферы, а из компонент вектора напряженности электрического поля в пространстве между обкладками конденсатора отличной от нуля оказывается только радиальная компонента. Действительно, циркуляция вектора 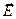по любому замкнутому контуру равна нулю, рассматриваем произвольный замкнутый контур на промежуточной сфере a <r < b, циркуляция вектора напряженности представляет собой интеграл от касательной компоненты вектора 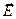, в силу произвольности контура заключаем, что равна нулю подынтегральная функция. В в качестве контрольной поверхности для применения теоремы Гаусса удобно выбрать именно промежуточную сферу радиуса r (этом случае 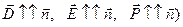. В итоге имеем:

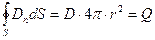. (1)

Из полученного уравнения имеем:

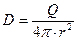, (a < r < b) . (2)

Используя соотношение (2), получаем расчётные зависимости для радиальных компонент векторов напряженности электрического поля и поляризованности среды:

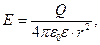(a < r < b) , (3)

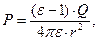(a < r < b) . (4)

Зависимость (3) позволяет рассчитать падение напряжения на обкладках сферического конденсатора:

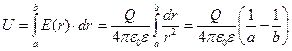. (5)

Для ёмкости сферического конденсатора получаем выражение:

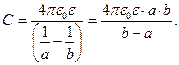(6)

Для сферического конденсатора с малым зазором между обкладками (b-a) произведение 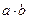приближённо равно величине a² . Отсюда следует, что и сферический конденсатор с малым зазором приближённо можно рассматривать как плоский конденсатор с соответствующими площадью обкладок и зазором между обкладками.

Вычислим величины поверхностной плотности связанных электрических зарядов на обкладках конденсатора, используя соотношения для электрических величин на поверхностях раздела:

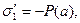
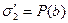, (7)

и вычислим сумму поверхностных связанных зарядов на обкладках сферического конденсатора:

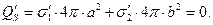(8)

Поскольку суммарный связанный заряд пространства, заполненного диэлектриком, должен равняться нулю, из результата (8) в рассматриваемом случае ( 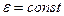) должно следовать, что суммарный объёмный заряд связанных электрических зарядов сферического конденсатора равен нулю. Это действительно так. Вычислим объёмную плотность связанных электрических зарядов:

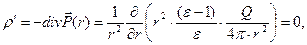(a < r < b) . (9)

Результат (9) получен с использованием выражения для дивергенции вектора в сферической системе координат с учетом того, что вектор имеет только радиальную компоненту, отличную от нуля.