Движение вдоль силовой линии.

Движение заряженных частиц в электромагнитном поле.

В настоящем разделе рассмотрим особенности движения в вакууме частиц, обладающих электрическим зарядом, в электрическом, магнитном или электромагнитном поле. Будем предполагать, что рассматриваемые частицы настолько слабо взаимодействуют друг с другом, что движение каждой частицы можно рассматривать отдельно от движения остальных частиц. Будем считать, что частица является материальной точкой, электрический заряд частицы не изменяется в процессе движения. Внешнее по отношению к частице электромагнитное поле является заданным, т.е. полностью определенным. Из внешних сил, действующих на заряженную частицу, будем учитывать только обобщённую силу Лоренца. При описании движения заряженной частицы будем исходить из классической механики Ньютона-Лагранжа или при необходимости из релятивистской механики.

Движение заряженных частиц в электрическом поле.

Движение заряженных частиц в электрическом поле постоянной напряжённости.

Движение заряженной частицы в однородном электростатическом поле может происходить как без пересечения силовых линий (более простой случай для анализа), так и с пересечением силовых линий напряжённости электростатического поля. В элементарном курсе физики изучается движение заряженной частицы в поле плоского конденсатора в приближении классической механики: скорость частицы значительно меньше скорости света в вакууме. В космической физике, астрофизике, физике элементарных частиц (физика высоких энергий) эти условия могут оказаться не выполненными. В современных физических установках скорости элементарных частиц могут быть сравнимыми со скоростью света в вакууме (установки исследования космических лучей, ускорители и т.п.). Ниже при изучении движения заряженных частиц в однородном электростатическом поле будем использовать релятивистское приближение.

Движение вдоль силовой линии.

Пусть в безграничном пространстве имеет место стационарное однородное электрическое поле, вектор напряженности которого 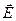определяет «продольное» направление. Расстояния вдоль этого направления описываются координатой х. Материальная точка (частица) с массой покоя 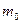и электрическим зарядом 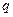в начальный момент времени 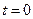начинает двигаться в продольном направлении с начальным импульсом 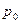. Уравнения движения в рамках СТО (релятивистский случай) имеют вид

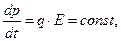
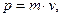
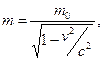(1)

где с – скорость света в вакууме, 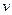- скорость движения частицы. Из системы уравнений (1) с учётом начального условия 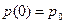получаем

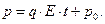(2)

В СТО имеет место легко проверяемое соотношение

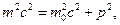(3)

из которого в рассматриваемом случае можно определить массу материальной частицы:

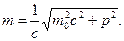(4)

Располагая зависимостью (2) и выражением (4), запишем зависимость скорости частицы от времени и одновременно дифференциальное уравнение для текущей координаты материальной точки:

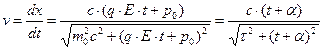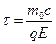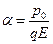, , . (5)

Величины 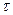и 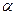в зависимости (5) имеют размерность времени. Качественное

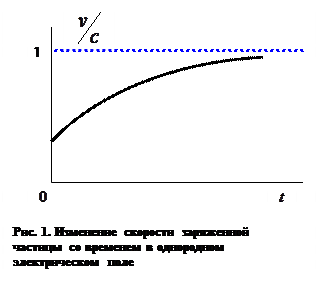графическое изображение зависимости

(5) приведено на рис. 1. При стремлении времени движения к бесконечности скорость частицы стремится к скорости света в вакууме. В отличие от классического случая, зависимость скорости от времени не является линейной.

Если движение материальной точки начиналось из начала координат, зависимость x=x(t) имеет вид: 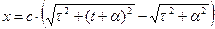. (6)

Значение координаты частицы с течением времени увеличивается, но этот закон, естественно, тоже отличается от классического случая. Особенно это показательно при рассмотрении ускорения материальной частицы:

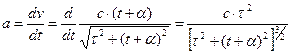. (7)

С течением времени ускорение материальной частицы уменьшается. В классическом случае эта величина должна была бы быть постоянной.

Интересно проверить, какой вид принимают зависимости (5), (6) и (7) при выполнении условия 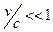. В этом случае имеет место оценка 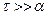(приближение «слабого поля») и время движения частицы должно быть невелико 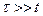. В рассматриваемом приближении

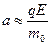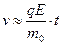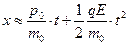, , . (8)

В приведённых зависимостях легко обнаружить закономерности равноускоренного движения частицы.