Распределение электрического заряда по поверхности уединённого проводника.
Изучение электростатики проводников затруднено тем, что распределение электрического заряда по наружной поверхности одного и того же проводящего тела в разных условиях может оказаться совершенно различным. Исключение составляет случай распределения электрического заряда по поверхности уединённого проводника в бесконечном однородном изотропном пространстве. Это распределение зависит только от формы граничной поверхности проводника. Ниже для простоты изложения будем рассматривать уединённые проводники в вакууме. У математиков задача о распределении электрического заряда по поверхности проводника носит название «задача Робена». Различают объёмный (трехмерный) случай и двумерный случай задачи Робена. В двумерном случае в качестве проводника рассматривают бесконечный цилиндр произвольного поперечного сечения. Вне проводника потенциал электростатического поля удовлетворяет уравнению Лапласа, на поверхности проводника потенциал обращается в нуль, а интеграл по поверхности проводника от нормальной производной потенциала пропорционален величине суммарного электрического заряда. В плоском (двумерном) случае для решения задачи Робена эффективны методы теории функций комплексного переменного, в частности, метод конформного отображения.
Допустим, что проводник является эллипсоидом, уравнение граничной поверхности которого описывается в декартовой системе координат уравнением
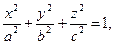
 (1)
(1)
Известно (Ф.Франк, Р.Мизес. Дифференциальные и интегральные уравнения математической физики. – Л.-М.: ОНТИ. Гл. редакция общетехнической литературы. – 1937.-998с., стр. 706) распределение поверхностной плотности электрического заряда по поверхности проводящего эллипсоида:
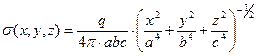 . (2)
. (2)
Из этого соотношения следует оценка
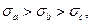 (3)
(3)
где 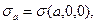
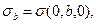
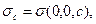 т.е. поверхностные плотности электрического заряда в точках пересечения осей эллипсоида с поверхностью. Если размер а очень велик, а размеры b и c малы, то
т.е. поверхностные плотности электрического заряда в точках пересечения осей эллипсоида с поверхностью. Если размер а очень велик, а размеры b и c малы, то 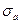 становится очень большой. Вспомним, что эта величина пропорциональна нормальной составляющей напряжённости электростатического поля вблизи поверхности проводника. Электрический пробой зависит от величины напряжённости электростатического поля. Получается, что пробой происходит в окрестности «острого» конца вытянутого в одном направлении эллипсоида.
становится очень большой. Вспомним, что эта величина пропорциональна нормальной составляющей напряжённости электростатического поля вблизи поверхности проводника. Электрический пробой зависит от величины напряжённости электростатического поля. Получается, что пробой происходит в окрестности «острого» конца вытянутого в одном направлении эллипсоида.
Для проводящего шара имеем
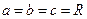 ,
, 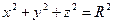
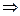
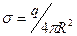 , (4)
, (4)
распределение поверхностной плотности электрического заряда является равномерным.
Неравномерность распределения электрического заряда по поверхности произвольного проводника является причиной погрешности, возникающей, например, при элементарном, упрощённом расчёте ёмкости конденсатора конечных размеров. Строгий учёт «краевых эффектов» иногда представляет собой довольно сложную задачу. В частности, вывод соотношения (2) требует введения эллипсоидальных координат, умения записать уравнение Лапласа в этих координатах, построить решение полученного уравнения в частных производных с переменными коэффициентами (т.е. получить распределение потенциала электростатического поля вне проводящего эллипсоида), вычислить напряжённость электростатического поля в окрестности граничной поверхности эллипсоида и, наконец, вычислить величину поверхностной плотности электрического заряда на поверхности проводящего эллипсоида. Только в редких исключительных случаях решение задач рассматриваемого типа можно получить в замкнутой аналитической форме, в остальных случаях решение получают с помощью численных методов, используя специальное программное обеспечение современных компьютеров.
| <== предыдущая лекция | | | следующая лекция ==> |
| Напряжённость и потенциал электростатического поля внутри и снаружи проводника. | | | Сосредоточенный электрический заряд над бесконечной проводящей плоскостью. |
Дата добавления: 2017-09-01; просмотров: 2025;











