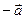Сосредоточенный электрический заряд над бесконечной проводящей плоскостью.

Проводник во внешнем электростатическом поле.

Электрический заряд, расположенный вне проводника, оказывает на него специфическое действие: на поверхности проводника возникает индуцированная поверхностная плотность электрического заряда даже в том случае, когда изначально проводник не был заряжен. Подобное явление имеет место и при действии на проводник внешнего электростатического поля. Индуцированный на проводнике электрический заряд искажает внешнее изначальное электростатическое поле.

Сосредоточенный электрический заряд над бесконечной проводящей плоскостью.

Рассмотрим сосредоточенный электрический заряд величины 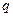, расположенный в пространстве на расстоянии 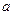над бесконечной проводящей плоскостью. Вследствие явления электростатической индукции на плоскости возникает индуцированный электрический заряд, распределение поверхностной плотности 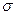которого необходимо определить. В пространстве над проводящей плоскостью потенциал электростатического поля должен удовлетворять уравнению Лапласа (кроме точки расположения заряда 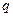), и принимать постоянное значение на проводящей плоскости. Пусть это значение будет равно нулю.

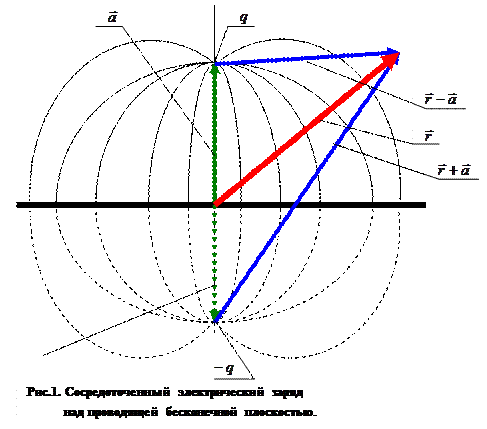
Распределение электростатического потенциала в пространстве над проводящей плоскостью (рис. 1) можно построить с помощью метода изображений: допустим, что в пространстве под проводящей плоскостью находится фиктивный сосредоточенный электрический заряд, равный по величине и противоположный по знаку, являющийся зеркальным отражением исходного заряда относительно проводящей плоскости. Поле совокупности исходного заряда и его зеркального изображения в пространстве над проводящей плоскостью является реальным электростатическим полем, поле совокупности исходного заряда и его зеркального изображения под проводящей плоскостью является фиктивным, реально под проводящей плоскостью потенциал электростатического поля везде равен нулю, напряженность электростатического поля под проводящей плоскостью тоже равна нулю. Говорят, что действие фиктивного заряда 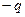эквивалентно действию индуцированного заряда, распределённого по проводящей плоскости. Если сравнить картину силовых линий и поверхностей уровня (эквипотенциальных поверхностей) электростатического поля в верхнем полупространстве для случая «заряд – плоскость» и случая «заряд – фиктивный заряд», то обнаружим их полное соответствие.

Убедимся в правильности наших построений. Пусть проводящая плоскость проходит через начало декартовой системы координат (x,y,z), ось z перпендикулярна проводящей плоскости, положение сосредоточенного заряда 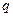определено радиус-вектором 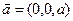, перпендикулярным проводящей плоскости. Положение фиктивного заряда - 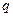определено радиус-вектором 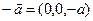. Если 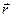- радиус-вектор точки наблюдения, имеют место следующие соотношения:

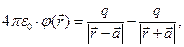
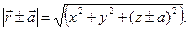(1)

Можно проверить прямым вычислением, что зависимость (1) удовлетворяет уравнению Лапласа для всех точек пространства над проводящей плоскостью (кроме случая 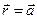) и стремится к нулю для бесконечно большого расстояния точки наблюдения от исходного заряда. Легко видеть, что при 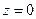(точка наблюдения расположена на проводящей плоскости) потенциал электростатического поля обращается в нуль для всех точек плоскости. В силу теоремы единственности другого решения задачи не существует.

Представляет интерес величина «поправки» распределения потенциала электростатического поля, возникающей из-за явления электростатической индукции:

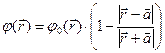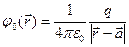, , (2)

здесь 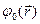- потенциал поля исходного сосредоточенного заряда. Может показаться, что рассматриваемая поправка существенна на расстояниях, сравнимых с величиной а, а на больших расстояниях от сосредоточенного заряда она не оказывает влияния на распределение потенциала исходного поля. На самом деле это не так. Действительно,

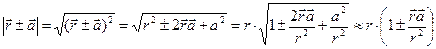, (3)

и поправка оказывается равной величине 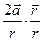. Второй сомножитель по величине не превышает единицу, а первый сомножитель обратно пропорционален величине r. Таким образом, индуцированный заряд кардинально меняет характер исходного электростатического поля: 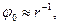а 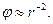Полученный результат характерен для потенциала поля электрического диполя.

Вычислим вектор напряжённости совокупного электростатического поля:

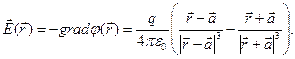(4)

Напряжённость электростатического поля, образованного сосредоточенным электрическим зарядом 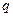в отсутствие проводящей плоскости, определяется выражением:

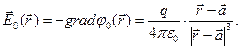(5)

Заметим, что и для вектора напряжённости суммарного электростатического поля влияние индуцированного электрического заряда существенно во всём пространстве: для случая 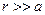имеют место асимптотические зависимости 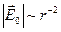, 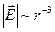. Покажем это непосредственным вычислением:

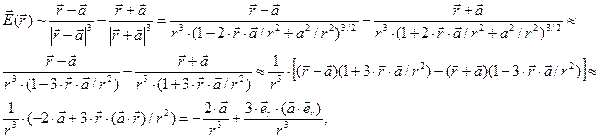
где 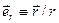- единичный безразмерный вектор вдоль направления радиус-вектора точки наблюдения. Этот результат характерен для величины напряжённости поля электрического диполя.

Составляющие вектора напряжённости 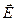для произвольной точки пространства над проводящей плоскостью (z>0) имеют вид:

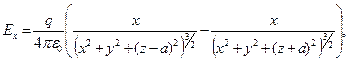
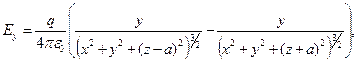(6)

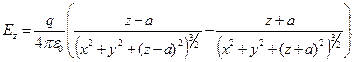
Для точек проводящей плоскости z=0 получаем:

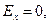
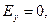
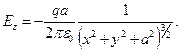(7)

Как и следовало ожидать, касательные к проводящей плоскости компоненты вектора напряжённости электростатического поля обращаются в нуль, а нормальная к проводящей плоскости компонента остаётся единственной отличной от нуля. В соответствии с теоремой Гаусса для вектора напряжённости 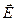получаем зависимость распределения поверхностной плотности электрического заряда по плоскости z=0:

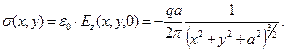(8)

Заметим, что соотношение (8) получено при использовании физически реального распределения напряжённости электростатического поля в пространстве выше и ниже проводящей плоскости: напряжённость электростатического поля в нижнем полупространстве равна нулю.

На малых расстояниях от оси симметрии задачи имеет место асимптотическое разложение

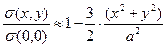. (9)

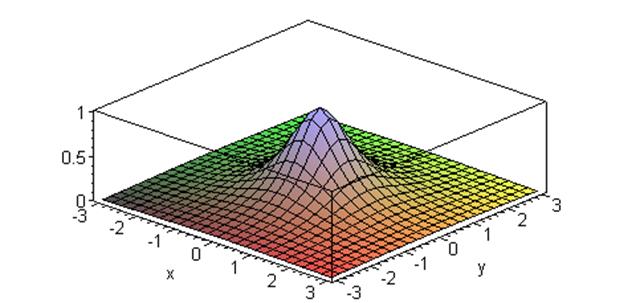
На рис. 2 показано распределение отношения величины локальной поверхностной плотности индуцированного электрического заряда по поверхности проводящей пластины

к величине поверхностной плотности индуцированного заряда в начале координат, вдоль осей x и y отложены расстояния, деленные на расстояние а от плоскости до исходного сосредоточенного заряда.

Заметим, что на проводящей плоскости имеет место индуцированный электрический заряд, знак которого противоположен знаку исходного сосредоточенного заряда. Интересно вычислить его величину. Для этого проинтегрируем полученное выражение по площади проводящей плоскости. Используя полярную систему координат ( 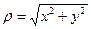) и условие осевой симметрии распределения поверхностной плотности индуцированного заряда, получаем:

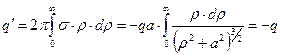. (10)

На проводящей плоскости распределён индуцированный электрический заряд, равный по величине исходному сосредоточенному заряду и обратный ему по знаку заряда.