Алгебраические фракталы

Это самая крупная группа фракталов. Неожиданностью для математиков стала возможность с помощью примитивных алгоритмов порождать очень сложные небанальные структуры.

Примером таких фракталов может служить:

Множество Мандельброта

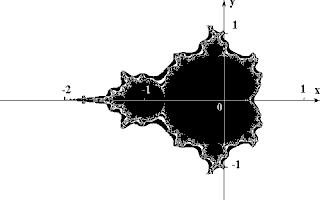
Участок границы множества Мандельброта, увеличенный в 200 pаз.

Множества Жюлиа

Кривая Пеано

Треугольник Серпинского

Лоренцевы аттракторы

Губка Серпинского

Получают их с помощью нелинейных процессов в n-мерных пространствах. Наиболее изучены двухмерные процессы. Известно, что нелинейные динамические системы обладают несколькими устойчивыми состояниями. Состояние, в котором оказалась динамическая система после некоторого числа повторов одной операции, зависит от ее начального состояния. Поэтому каждое устойчивое состояние (или как говорят - аттрактор) обладает некоторой областью начальных состояний, из которых система обязательно попадет в рассматриваемые конечные состояния. Таким образом фазовое пространство системы разбивается на области притяжения аттракторов.Аттракторы - центры ведущие борьбу за доминирование на плоскости. Между аттракторами возникает граница представляющая витееватый узор.

Если фазовым является двухмерное пространство, то окрашивая области притяжения различными цветами, можно получить цветовой фазовый портрет этой системы. Меняя алгоритм выбора цвета, можно получить сложные фрактальные картины с причудливыми многоцветными узорами.