Стохастические фракталы

Еще одним известным классом фракталов являются стохастические фракталы, которые получаются в том случае, если в процессе случайным образом менять какие-либо его параметры. При этом получаются объекты очень похожие на природные - несимметричные деревья, изрезанные береговые линии и т.д. Двумерные стохастические фракталы используются при моделировании рельефа местности и поверхности моря.

Стохастические фракталы

Словарь терминов

Геометрия фракталов - англ. fractal geometry
метод технического анализа. Согласно представлениям Г.ф., графики цен состоят из идентичных универсальных элементов - фракталов и потому имеют одинаковый вид вне зависимости от того, какой интервал времени рассматривается (неделя, месяц или год).

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную оттопологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев.

Фракталы - геометрические фигуры, полученные путем дробления на части, подобные целому, но имеющие свои отличительные черты.

В нелинейной динамике Фракталов возникают как аттракторы у диссипативных динамических систем. Аттракторами наз. множества в фазовом пространстве, притягивающие траектории динамич. системы. При этом, если аттрактор является Фракталом, его наз. странным аттрактором. Существование странных аттракторов является типичным свойством диссипативных динамич. систем. В случае дискретных отображений примером может служить аттрактор Фейгенба-ума (см.Фейгенбаума универсальность). Хорошо изучен механизм образования и свойства аттрактора Лоренца (Е. Lorenz), отвечающего системе ур-ний Лоренца

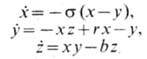
при значениях параметров r=28, b=⁸/₃, s=10[2]. Локально аттрактор Лоренца имеет структуру прямого произведения канторова множества на двумерную плоскость (т. н. книга Лоренца). Наиб. важным примером фрактальных аттракторов являются странные аттракторы, возникающие в ур-ниях Навье - Стокса ([3], [4]).

задачи