Отображения множеств
Если каждому элементу x множества X поставлен в соотвествие ровно один элемент f(x) множества Y, то говорят, что задано отображение f из множества X в множество Y. При этом, если f(x) = y, то элемент y называется образом элемента x при отображении f, а элемент x называется прообразом элемента y при отображении f. Обозначение: f: X Y.
11. Нарисуйте всевозможные отображения из множества {7,8,9} в множество {0,1}.
Пусть f: X Y, y Y, A X, B Y. Полным прообразом элемента y при отображении f называется множество {x X | f(x) = y}. Обозначение: f 1(y). Образом множества A X при отображении fназывается множество {f(x) | x A}. Обозначение: f(A). Прообразом множества B Y называется множество {x X | f(x) B}. Обозначение: f 1(B).
12. Для отображения f: {0,1,3,4} {2,5,7,18}, заданного картинкой, найдите f({0,3}), f({1,3,4}), f 1(2), f 1({2,5}), f 1({5,18}).
а) 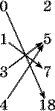 б) б) 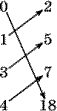 в) в) 
|
13. Пусть f: X Y, A1, A2 X, B1, B2 Y. Всегда ли верно, что
а) f(X) = Y;
б) f 1(Y) = X;
в) f(A1A2) = f(A1)f(A2);
г) f(A1A2) = f(A1)f(A2);
д) f 1(B1 B2) = f 1(B1) f 1(B2);
е) f 1(B1B2) = f 1(B1)f 1(B2);
ж) если f(A1) f(A2), то A1 A2;
з) если f 1(B1) f 1(B2), то B1 B2?
Композицией отображений f: X Y и g: Y Z называется отображение, сопоставляющее элементу x множества X элемент g(f(x)) множества Z. Обозначение: gf.
14. Докажите, что для произвольных отображений f: X Y, g: Y Z и h: Z W выполняется следующее: h(gf) = (hg)f.
15. Пусть f: {1,2,3,5} {0,1,2}, g: {0,1,2} {3,7,37,137}, h: {3,7,37,137} {1,2,3,5}– отображения, показанные на рисунке:
f: 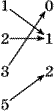 g: g: 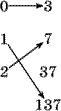 h: h: 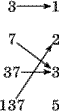
|
Нарисуйте картинки для следующих отображений:
а) gf; б) hg; в) fhg; г) ghf.
Отображение f: X Y называется биективным, если для каждого y Y найдется ровно один x X такой, что f(x) = y.
16. Пусть f: X Y, g: Y Z. Верно ли, что если f и g биективны, то и gf биективно?
17. Пусть f: {1,2,3} {1,2,3}, g: {1,2,3} {1,2,3}, – отображения, изображенные на рисунке:
f: 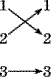 g: g: 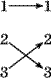
|
Нарисуйте картинки для следующих отображений:
| а) gfg; | б) fgf; | в) fgfgfg. |
18. Про каждые два из следующих множеств выясните, существует ли биекция из первого во второе (надлежит считать, что ноль – натуральное число):
а) множество натуральных чисел;
б) множество четных натуральных чисел;
в) множество натуральных чисел без числа 3.
Список литературы
P. M. Кроновер. Фракталы и хаос в динамических системах. Основы теории. М., 2000. — 352 с
3. Федер Е. Фракталы. Пер. с англ.-М.: Мир,1991.-254с.
(Jens Feder, Plenum Press, NewYork, 1988)
4. Application of fractals and chaos. 1993, Springer-Verlag, Berlin.
Дата добавления: 2021-09-07; просмотров: 715;











