Тема 5. Случайные фракталы. Применение фракталов при моделировании физических процессов

Все объекты, с которыми сталкивается человек, можно разделить на искусственные и естественные. Все искусственные объекты имеют, как правило, четкие формы, в то время как формы естественных объектов в большинстве своем являются неправильными. Поэтому такие образования, как горные хребты, береговые линии или облака не обладают подобием, в смысле неизменностью, при линейном увеличении или уменьшении. При изменении масштаба рассмотрения объектов случайным образом меняются их отдельные элементы. Принцип самоподобия в приведенных случаях необходимо рассматривать со статистических позиций, то есть понятие «подобный» необходимо толковать как «похожий».

Отдельную группу, предназначенную для моделирования природных объектов, образуют случайные фракталы. Наиболее наглядным случайным фракталом является рандомизированная снежинка Кох. Для ее получения достаточно на каждом шаге итерационного процесса обращать вовнутрь или наружу вершину нового строящегося треугольника (рис. 2.17).

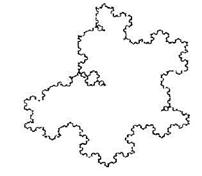
Рисунок 2.17 – Рандомизированная кривая Кох

Фрактальная размерность построенной таким образом кривой остается прежней. Предельная кривая рандомизированной снежинки Кох может служить прекрасной моделью, например, контура облака или острова. Аналогичный подход может быть реализован при построении фракталов с помощью L-систем, когда случайным образом реализуется, например, операция ветвления. Построенные таким образом деревья, растения или снежинки будут иметь более естественный вид. В приведенных примерах рандомизации подвергаются лишь отдельные параметры итерационного процесса, в то время как сам алгоритм (система итерированных функций) построения фракталов остается неизменным – детерминированным.

Очевидно, что итерационный процесс также может быть случайным. Для того, чтобы в результате этого процесса осуществлялось построение именно фракталов, необходимо выполнение принципа статистического самоподобия. Свойством статистического самоподобия обладает винеровский процесс (броуновское движение), имеющий нормальное распределение.

Винеровский процесс является марковским («будущее» процесса не зависит от «прошлого»), если значение процесса в текущий момент времени зависит только от значений в предыдущий момент времени и величины приращения. Пример винеровского процесса показан на рисунке 2.18.

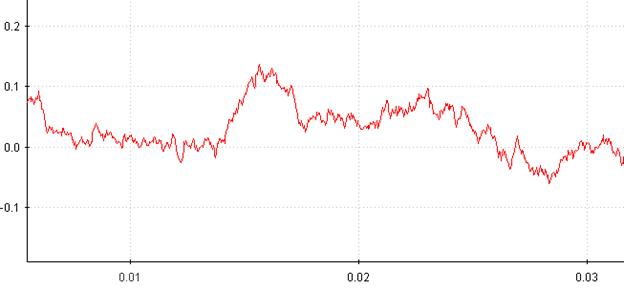
Рисунок 2.18 – График винеровского процесса во времени

Говоря формально, некоторая переменная z подчиняется винеровскому процессу, если она имеет следующие свойства.

Свойство 1. Изменение Δz на протяжении малого промежутка времени Δt удовлетворяет равенству:

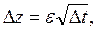(2.21)

где ε – случайная величина, подчиняющаяся стандартному нормальному распределению ø (0,1), 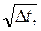– стандартное отклонение, зависящее от времени процесса.

Свойство 2. Величины Δz на двух малых промежутках времени Δt являются независимыми.

Из первого свойства следует, что величина Δz имеет нормальное распределение, у которого математическое ожидание равно нулю, стандартное отклонение равно 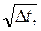а дисперсия равна Δt.

Второе свойство означает, что величина z подчиняется марковскому процессу (независимости одного распределения от другого).

Квадратный корень получается из-за того, что при анализе марковского процесса дисперсии изменений переменной в последовательные моменты складываются, а стандартные отклонения – нет. Если дисперсия изменений переменной в течение одного года равна 1,0, то дисперсия изменений этой переменной в течение двух лет будет равна 2,0, а через три года – 3,0. 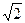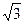В то же время стандартные отклонения изменений переменных через два и три года будут равны и , соответственно. Строго говоря, мы не должны говорить, что стандартное отклонение изменений переменной за один год равно 1,0 в год. Следует говорить, что оно равно «корню квадратному из единицы в год». Это объясняет, почему величину неопределенности часто считают пропорциональной квадратному корню из времени.

Приращения винеровского процесса обладают свойствами статического самоподобия. Для них справедливо:

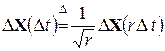, (2.22)

или

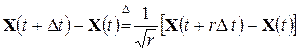
для любого .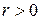

Здесь величина 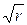является коэффициентом статистического самоподобия, а символ 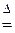означает, что две случайные величины имеют одинаковые дифференциальные законы распределения.

Определим фрактальную размерность винеровского процесса. Без потери общности полагаем, что значения аргумента находятся в интервале [0,1]. Разделим этот интервал на п равных подинтервалов одинаковой длины 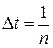и таким же образом разделим вертикальную ось на подинтервалы длины 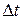, как показано на рисунке 2.19.

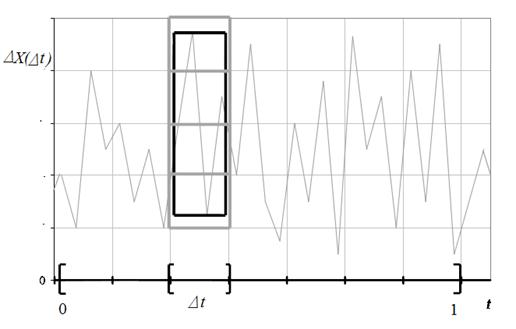
Рисунок 2.19 – Клеточное покрытие функции на подинтервале

Выражение 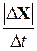будет служить в качестве оценки числа квадратов 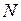размера 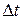, необходимых для покрытия части графика 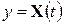, расположенной над одним подинтервалом. Это число пропорционально 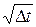– отклонению (многие считают квадратный корень из времени величиной неопределенности).

Всего имеется 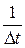таких подинтервалов, поэтому общее число квадратов пропорционально 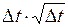= 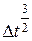, то есть:

.

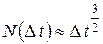Таким образом, фрактальная размерность винеровского процесса:

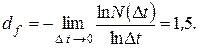
Наиболее удобно фрактальный винеровский процесс определить при помощи параметра Херста 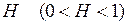, который характеризует уровень самоподобия для случайного процесса. При 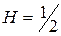фрактальный винеровский процесс совпадает с классическим винеровским процессом. В таком случае фрактальная размерность и параметр H связываются выражением:

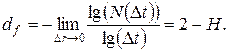(2.23)

Как видно из (2.23), изменяя параметр Н, можно менять фрактальную размерность.

Визуально можно отметить следующие изменения в реализациях фрактального винеровского процесса для различных значений Н (рис. 2.20). Увеличение Н приводит не только к уменьшению 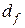, но и к уменьшению дисперсии процесса, то есть он становится менее «изрезанным», более гладким, с небольшими отклонениями от математического ожидания. Изменяя Н, можно менять вид случайного фрактала.

Применение фракталов

Применение фракталов

Компьютерная графика

Физика и другие естественные науки

Сжатие изображений

Анализ рынков

Другие применения

Компьютерная графика

Фракталы широко применяются в компьютерной графике для построения изображений природных объектов, таких, как деревья, кусты, горные ландшафты, поверхности морей и так далее.

С использованием фракталов могут строиться не только ирреальные изображения, но и вполне реалистичные (например, фракталы нередко используются при создании облаков, снега, береговых линий, деревьев и кустов и др.). Поэтому применять фрактальные изображения можно в самых разных сферах, начиная от создания обычных текстур и фоновых изображений и кончая фантастическими ландшафтами для компьютерных игр или книжных иллюстраций. А создаются подобные фрактальные шедевры (равно как и векторные) путем математических расчетов, но в отличие от векторной графики базовым элементом фрактальной графики является сама математическая формула - это означает, что никаких объектов в памяти компьютера не хранится, и изображение (как бы ни было оно замысловато) строится исключительно на основе уравнений.

Физика и другие естественные науки

В физике фракталы естественным образом возникают при моделировании нелинейных процессов, таких, как турбулентное течение жидкости, сложные процессы диффузии-адсорбции, пламя, облака и т. п. Фракталы используются при моделировании пористых материалов, например, в нефтехимии. В биологии они применяются для моделирования популяций и для описания систем внутренних органов (система кровеносных сосудов). уравнений.

Сжатие изображений

Фрактальное сжатие изображений — это алгоритм сжатия изображений c потерями, основанный на применении систем итерируемых функций (IFS, как правило являющимися аффинными преобразованиями) к изображениям. Данный алгоритм известен тем, что в некоторых случаях позволяет получить очень высокие коэффициенты сжатия (лучшие примеры — до 1000 раз при приемлемом визуальном качестве) для реальных фотографий природных объектов, что недоступно для других алгоритмов сжатия изображений в принципе. Из-за сложной ситуации с патентованием широкого распространения алгоритм не получил

Сжатие изображений

Фрактальное сжатие изображений — это алгоритм сжатия изображений c потерями, основанный на применении систем итерируемых функций (IFS, как правило являющимися аффинными преобразованиями) к изображениям. Данный алгоритм известен тем, что в некоторых случаях позволяет получить очень высокие коэффициенты сжатия (лучшие примеры — до 1000 раз при приемлемом визуальном качестве) для реальных фотографий природных объектов, что недоступно для других алгоритмов сжатия изображений в принципе. Из-за сложной ситуации с патентованием широкого распространения алгоритм не получил.

Суть фрактального сжатия

Основа метода фрактального кодирования — это обнаружение самоподобных участков в изображении. Впервые возможность применения теории систем итерируемых функций (IFS) к проблеме сжатия изображения была исследована Майклом Барнсли (Michael Barnsley) и Аланом Слоуном (Alan Sloan). Они запатентовали свою идею в 1990 и 1991 гг (U.S. Patent 5,065,447 (англ.)). Джеквин (Jacquin) представил метод фрактального кодирования, в котором используются системы доменных и ранговых блоков изображения (domain and range subimage blocks), блоков квадратной формы, покрывающих все изображение. Этот подход стал основой для большинства методов фрактального кодирования, применяемых сегодня. Он был усовершенствован Ювалом Фишером (Yuval Fisher) и рядом других исследователей. В соответствии с данным методом изображение разбивается на множество неперекрывающихся ранговых подизображений (range subimages) и определяется множество перекрывающихся доменных подизображений (domain subimages). Для каждого рангового блока алгоритм кодирования находит наиболее подходящий доменный блок и аффинное преобразование, которое переводит этот доменный блок в данный ранговый блок. Структура изображения отображается в систему ранговых блоков, доменных блоков и преобразований.

Идея заключается в следующем: предположим что исходное изображение является неподвижной точкой некоего сжимающего отображения. Тогда можно вместо самого изображения запомнить каким-либо образом это отображение, а для восстановления достаточно многократно применить это отображение к любому стартовому изображению.

По теореме Банаха, такие итерации всегда приводят к неподвижной точке, то есть к исходному изображению. На практике вся трудность заключается в отыскании по изображению наиболее подходящего сжимающего отображения и в компактном его хранении. Как правило, алгоритмы поиска отображения (то есть алгоритмы сжатия) в значительной степени переборные и требуют больших вычислительных затрат. В то же время, алгоритмы восстановления достаточно эффективны и быстры. Вкратце метод, предложенный Барнсли, можно описать следующим образом. Изображение кодируется несколькими простыми преобразованиями (в нашем случае аффинными), то есть определяется коэффициентами этих преобразований (в нашем случае A, B, C, D, E, F).

Например, изображение кривой Коха можно закодировать четырмя аффинными преобразованиями, мы однозначно определим его с помощью всего 24-х коэффициентов. Далее, поставив чёрную точку в любой точке картинки мы будем применять наши преобразования в случайном порядке некоторое (достаточно большое) число раз (этот метод ещё называют фрактальный пинг-понг).

В результате точка обязательно перейдёт куда-то внутрь чёрной области на исходном изображении. Проделав такую операцию много раз мы заполним все чёрное пространство, тем самым восстановив картинку.

Основная сложность метода

Основная сложность фрактального сжатия заключается в том, что для нахождения соответствующих доменных блоков вообще говоря требуется полный перебор. Поскольку при этом переборе каждый раз должны сравниваться два массива, данная операция получается достаточно длительной. Сравнительно простым преобразованием её можно свести к операции скалярного произведения двух массивов, однако даже скалярное произведение считает сравнительно длительное время. На данный момент известно достаточно большое количество алгоритмов оптимизации перебора, возникающего при фрактальном сжатии, поскольку большинство статей, исследовавших алгоритм были посвящены этой проблеме, и во время активных исследований (1992—1996 года) выходило до 300 статей в год. Наиболее эффективными оказались два направления исследований: метод выделения особенностей (feature extraction) и метод классификации доменов (classification of domains).

Патенты

Майклом Барнсли и другими было получено несколько патентов на фрактальное сжатие в США и других. Например, U.S. Patent 4,941,193 (англ.), 5,065,447 (англ.), 5,384,867 (англ.), 5,416,856 (англ.) и 5,430,812 (англ.). Эти патенты покрывают широкий спектр возможных изменений фрактального сжатия и серьёзно сдерживают его развитие.

Данные патенты не ограничивают исследований в этой области, то есть можно придумывать свои алгоритмы на основе запатентованных и публиковать их. Также можно продавать алгоритмы в страны, на которые не распространяются полученные патенты. Кроме того срок действия большинства патентов — 17 лет с момента принятия и он истекает для большинства патентов в ближайшее время, соответственно использование методов, покрывавшихся этими патентами станет гарантированно свободным

Анализ рынков

Последнее время фракталы стали популярным инструментом у трейдеров для анализа состояния биржевых рынков. Фракталы рынка являются одним из индикаторов в торговой системе Била Вильямса. Считается, что он же впервые и ввел это название в трейдинг. При торговле по фракталам, в сочетании со своим индикатором Аллигатор, автор обнаруживал локальные максимумы или минимумы рынка.

Теория фракталов на рынке в свое время вызвала бурные споры, прежде всего, потому что автор, как считают многие, вставил в свою теорию много научной терминологии (фрактал, аттрактор и т.д.), и сделал это не совсем корректно. Поскольку фракталы Вилямса появляются на рынке достаточно часто и практически на всех временных таймфреймах и являются, по сути, простыми локальными экстремумами на отрезке из 5 баров и практически не соответствуют математической теории фракталов. Точно таким же образованием на графике являются и ТД-точки второго порядка Томаса Демарка. Однако, несмотря все эти совпадения это теория весьма популярна и до сих пор.

Совсем не обязательно чтобы баров было пять (5 – минимальное количество баров для формирования фрактала на рынке) и чтобы, например, для фрактала вверх максимумы, начиная от центрального (самого высшего) бара последовательно снижались. Так же необязательным условием является то, что у центрального бара фрактала «вверх» минимум, как и максимум, был выше остальных.

Если в формации два бара имеют максимумы и оба эти максимума самые высокие, то второй максимальный бар не учитывается в расчетах при торговле по фракталам. То же самое касается и минимумов для фрактала вниз.

Прорывом покупателей у Била Вильямса считается выход цены за переделы фрактала вверх хотя бы на один пункт. Соответственно прорывом продавцов считается выход цены за пределы фрактала вниз хотя бы на один пункт. Классически, по Билу Вильямсу фрактал используют для прорывной стратегии, хотя в техническом анализе есть и обратные контртрендовые стратегии, использующие схожие шаблоны цен.Прорывы покупателей и продавцов является непосредственными торговыми сигналами, т.е. чуть выше фрактала вверх ставится ордер на покупку, ордер на продажу ставится чуть ниже фрактала вниз. При такой стратегии торговли по фракталам ордер стоп-лосс (Stop-Loss) ставится на самом удаленном фрактальном экстремуме из двух последних фракталов, направленных в противоположную сторону. Обычно (но не всегда) это предпоследний противоположный фрактал. Например, стоп-лосс (Stop-Loss) для позиции на покупку ставится на самом низком из двух последних фракталов, соответственно стоп-лосс для на позицию на продажу ставится на самом высоком из двух последних фракталов вверх.

В системе Вильямса фрактал на рынке используется не отдельно, а в сочетании с индикатором Аллигатор. При этом определенное направление и Аллигатора и фрактала являются обязательными принятии решения о сделке. Например, сделка при пробитии фрактала вверх осуществляется, только если фрактал находится выше Зубов Аллигатора. А сделка на продажу осуществляется, только если фрактал находится ниже Зубов Аллигатора. Таким образом, фрактал и Аллигатор являются двумя подтверждающими друг друга индикаторами.

Литература

Среди литературных произведений находят такие, которые обладают текстуальной, структурной или семантической фрактальной природой. В текстуальных фракталах потенциально бесконечно повторяются элементы текста:

неразветвляющееся бесконечное дерево, тождественное само себе с любой итерации («У попа была собака…», «Притча о философе, которому снится, что он бабочка, которой снится, что она философ, которому снится…», «Ложно утверждение, что истинно утверждение, что ложно утверждение…»)

неразветвляющиеся бесконечные тексты с вариациями («У Пегги был весёлый гусь…») и тексты с наращениями («Дом, который построил Джек»).

В структурных фракталах схема текста потенциально фрактальна:

венок сонетов (15 стихотворений), венок венков сонетов (211 стихотворений), венок венков венков сонетов (2455 стихотворений)

«рассказы в рассказе» («Книга тысячи и одной ночи», Я. Потоцкий «Рукопись, найденная в Сарагосе»)

предисловия, скрывающие авторство (У. Эко «Имя розы»)

Т. Стоппард «Розенкранц и Гильденстерн мертвы» (сцена с представлением перед королём).

В семантических и нарративных фракталах автор рассказывает о бесконечном подобии части целому:

Х. Л. Борхес «В кругу развалин»

Х. Кортасар «Жёлтый цветок»

Ж. Перек «Кунсткамера»

Радиотехника

Использование фрактальной геометрии при проектировании антенных устройств было впервые применено американским инженером Натаном Коэном, который тогда жил в центре Бостона, где была запрещена установка внешних антенн на здания. Натан вырезал из алюминиевой фольги фигуру в форме кривой Коха и наклеил её на лист бумаги, затем присоединил к приёмнику. Оказалось, что такая антенна работает не хуже обычной. И, хотя физические принципы работы такой антенны не изучены до сих пор, это не помешало Коэну основать собственную компанию и наладить их серийный выпуск.

Децентрализованные сети

Система назначения IP-адресов в сети Netsukuku использует принцип фрактального сжатия информации для компактного сохранения информации об узлах сети. Каждый узел сети Netsukuku хранит всего 4 Кб информации о состоянии соседних узлов, при этом любой новый узел подключается к общей сети без необходимости в центральном регулировании раздачи IP-адресов, что, например, характерно для сети Интернет. Таким образом, принцип фрактального сжатия информации гарантирует полностью децентрализованную, а следовательно, максимально устойчивую работу всей сети.

Роль фракталов сегодня достаточно велика в машинной графике. Фракталам посвящены тысячи публикаций и огромные ресурсы интернет, однако для многих специалистов далеких от информатики данный термин представляется абсолютно новым.

Фракталы приходят на помощь, например, когда требуется, с помощью нескольких коэффициентов, задать линии и поверхности очень сложной формы. С точки зрения машинной графики, фрактальная геометрия незаменима при генерации искусственных облаков, гор, поверхности моря. Фрактальная наука еще очень молода, и ей предстоит большое будущее. Красота фракталов далеко не исчерпана и еще подарит нам немало шедевров.

http://stu.sernam.ru/book_fah.php?id=77 броуновское движение и т.д.

Тема 6. Теория размерности

Размерность Хаусдорфа — естественный способ определить размерность подмножества в метрическом пространстве. Размерность Хаусдорфа согласуется с нашими обычными представлениями о размерности в тех случаях, когда эти обычные представления есть. Например, в трёхмерном евклидовом пространствехаусдорфова размерность конечного множества равна нулю, размерность гладкой кривой — единице, размерность гладкой поверхности — двум и размерность множества ненулевого объёма — трём. Для более сложных (фрактальных) множеств размерность Хаусдорфа может не быть целым числом.

Определение

Определение размерности Хаусдорфа состоит из нескольких шагов. Пусть — ограниченное множество в метрическом пространстве .

-покрытия

Пусть . Не более чем счётный набор подмножеств пространства будем называть -покрытием множества , если выполнены следующие два свойства:

·

· для любого : (здесь и далее означает диаметр множества ).

-мера Хаусдорфа

Пусть . Пусть — покрытие множества . Определим следующую функцию, в некотором смысле показывающую «размер» этого покрытия: .

Обозначим через «минимальный размер» -покрытия множества : , где инфимум берётся по всем -покрытиям множества .

Очевидно, что функция (нестрого) возрастает при уменьшении , поскольку при уменьшении мы только сжимаем множество возможных -покрытий. Следовательно, у неё есть конечный или бесконечный предел при :

.

Величина называется -мерой Хаусдорфа множества .

Свойства -меры Хаусдорфа

· -мера Хаусдорфа является борелевской мерой на .

· с точностью до умножения на коэффициент: 1-мера Хаусдорфа для гладких кривых совпадает с их длиной; 2-мера Хаусдорфа для гладких поверхностей совпадает с их площадью; -мера Хаусдорфа множеств в совпадает с их -мерным объёмом.

· убывает по . Более того, для любого множества существует критическое значение , такое, что:

o для всех

o для всех

Значение может быть нулевым, конечным положительным или бесконечным.

Определение размерности Хаусдорфа

Размерностью Хаусдорфа множества называется число из предыдущего пункта.

Примеры

Для самоподобных множеств размерность Хаусдорфа может быть вычислена явно. Неформально говоря, если множество разбивается на частей, подобных исходному множеству с коэффициентами , то его размерность является решением уравнения . Например,

· размерность множества Кантора равна (разбивается на две части, коэффициент подобия 1/3),

· размерность треугольника Серпинского — (разбивается на 3 части, коэффициент подобия 1/2),

· размерность кривой дракона — (разбивается на 2 части, коэффициент подобия ).

Свойства размерности Хаусдорфа

· Размерность Хаусдорфа любого множества не превосходит нижней и верхней размерностей Минковского.

· Размерность Хаусдорфа не более чем счётного объединения множеств равна макcимуму из их размерностей. В частности, добавление счётного множества к любому множеству не меняет его размерности.

См. также

· фрактал

· размерность Минковского

Аттракторы — это множества, к которым приближаются точки

при последовательных итерациях отображения. С отображениями рабо-

тать гораздо легче, чем с дифференциальными уравнениями. Если мы

хотим найти аттрактор, то нам не нужно вычислять эти итерации и ана-

лизировать наше отображение. Оно само найдёт свой аттрактор.

Размерность Хаусдорфа

Размерность Хаусдорфа обобщает понятие размерности действительного векторного пространства, и является естественным способом определения размерности подмножества в метрическом пространстве. Например размерность Хаусдорфа n-мерного (размерность в смысле векторного пространства) унитарного пространства (особый случай векторного пространства) будет тоже равна n. Хорошее математическое описание размерности Хаусдорфа дано в русской википедии, нам же важно понять смысл этой размерности интуитивно. Представим полное покрытие множества X шарами радиуса не более чем r, обозначим количество этих шаров за N( r ).

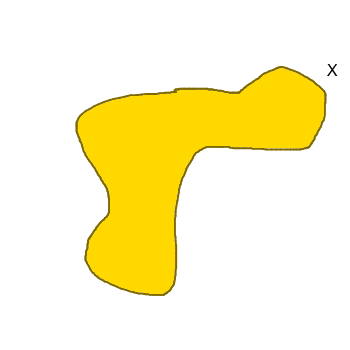
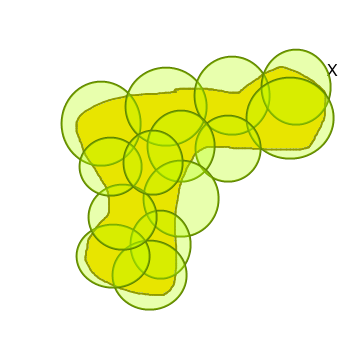
Значение N( r ) будет расти при уменьшении r (для полного покрытия будет требоваться все больше шаров). Размерностью Хаусдорфахорошего множества X будет являться такое уникальное число d, что N( r ) будет расти как 1/r^d при стремлении r к нулю. Под хорошим множеством понимаются гладкие множества без особенностей, какими например обладают фракталы. Примерами хороших множеств могут быть любые идеализированные геометрические объекты такие как куб, сфера и так далее.

Фрактальная размерность

Опишем один простой способ задания фрактальной размерности, хотя например размерность Минковского так же является одой из фрактальных размерностей, и она как раз тесно связана с размерностью Хаусдорфа, но об этом позже. Вот он простой способ задания фрактальной размерности:

· Возьмем некоторую D-мерную геометрическую структуру и будем делить итеративно ее стороны на M равных частей (на следующей итерации, будем делить каждую полученную на предыдущей итерации часть так же на M частей)

· Каждый уровень будет состоять из M^D частей предыдущего уровня

· Обозначим следующим образом количество полученных частей N = M^D

Выполним следующее преобразование для вычисления формулы для значения фрактальной размерности D:

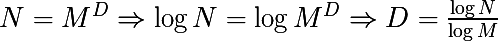
Рассмотрим простые примеры, которые я почерпнул из очень крутого курса по комплексным системам. Возьмем отрезок (одномерное ограниченное множество), разделим его на две равные части, таким же образом будем поступать с каждой полученной частью. Таким образом мы будем создавать полное покрытие множества.

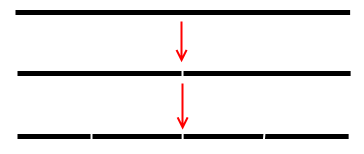
Т.е. M = 2 и N = 2, т.к. из каждой части производится два новых куска отрезка, вычислим D:

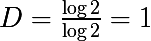
Если разделять отрезок не на 2 части, а на 3, то D все равно будет равна 1, т.к. M = 3 и N = 3. Эта размерность совпадает с размерностью Хаусдорфа для хорошего множества.

Давайте рассмотрим аналогичную процедуру для квадрата.

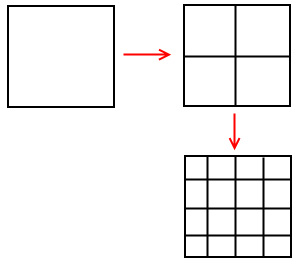
Получаем M = 2 и N = 4, т.к. разделяя стороны на 2 равные части, мы получаем 4 новых, вычислим фрактальную размерность

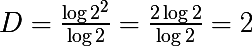
И опять полученная размерность совпала с размерностью Хаусдорфа. Такой же результат можно получить если делить стороны на 3 равные части и т.д.

Бенуа Мандельброт при исследовании реальных объектов сделал очевидное замечание:
В реальном мире мы редко имеем дело с идеализированными объектами, что же будет если мы рассмотрим не совсем хорошийгеометрический объект, например кривую Коха (не путать с палочкой), вспомним алгоритм генерации такого множества. На каждой новой итерации, каждый кусок кривой, который является прямым отрезком, делится на три равные части, затем средний кусок убирается, а на его место становится конструкция напоминающая перевернутую букву V, каждое ребро которой равно убранной части отрезка (а так же равно и оставшимся).
Другими словами M = 3, т.к. отрезок делится на три равные части, а N = 4, т.к. каждая часть превращается в 4 части равных 1/4 от оригинала. Тогда фрактальная размерность такого множества при бесконечном итерировании будет равна следующему значению:

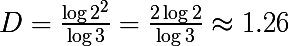
В качестве другого примера давайте глянем на треугольник Серпинского

На каждой итерации одна сторона делится на 2 части, т.е. M = 2, а в результате получается 3 части, т.е. N = 3, тогда

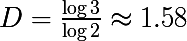
Возникает конечно вопрос, вот мы получили цифры некоторые, ну размерность стала дробной, и что? Есть ли в этом какой-то смысл, или это просто математические штучки. Строгой формулировки с описанием смысла дробности размерности нет, но можно ее интерпретировать следующим образом, на некотором интуитивном уровне. Фрактальная размерность чувствительна

ко всякого рода несовершенствам реальных объектов, позволяя различать и индивидуализировать то, что прежде было безлико и неразличимо (источник)

В курсе по анализу комплексных систем упоминается следующая трактовка: дробная размерность — это своего рода плотность самоподобия.

Но говоря о реальных объектах читатель сразу же скажет, но ведь и кривая Коха и треугольник Серпинского далеки от реальности, что же делать тогда? Как я упомянул выше, приведенное определение фрактальной размерности является простым, и одним из нескольких. Давайте перейдем к более сложному определению фрактальной размерности. А пока взгляните, например, на капусту брокколи Романеско, вот такая вот реальность.

Размерность Минковского

Размерность Минковского — это один из способов задания фрактальной размерности ограниченного множества в метрическом пространстве, определяется следующим образом:

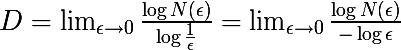
· где N(ε) минимальное число множеств диаметра ε, которыми можно покрыть исходное множество.

Если предел не существует, то рассматривают верхний и нижний пределы и говорят соответственно о верхней и нижней размерности Минковского. Верхняя и нижняя размерности Минковского тесно связанны с размерностью Хаусдорфа, интуитивно это легко уловить по способу задания размерности. Обычно упомянутые три размерности совпадают, и только в очень специфичных случаях имеет смысл их различать, но это не наши случаи.

Размерность Минковского имеет так же другое название — box-counting dimension, из-за альтернативного способа ее определения, который кстати дает подсказку к способу вычисления этой самой размерности. Рассмотрим двумерный случай, хотя аналогичное определение распространяется и на n-мерный случай. Возьмем некоторое ограниченное множество в метрическом пространстве, например черно-белую картинку, нарисуем на ней равномерную сетку с шагом ε, и закрасим те ячейки сетки, которые содержат хотя бы один элемент искомого множества.

Далее начнем уменьшать размер ячеек, т.е. ε, тогда размерность Минковского будет вычисляться по вышеприведенной формуле, исследуя скорость изменения отношения логарифмов. Эта фраза может быть не сразу понятна, но думаю все прояснит алгоритм, используемый для вычисления приближенного значения размерности Минковского.

Box-counting алгоритм

Алгоритм выводится следующим образом, обозначим за D_bc приближенное значение размерности Минковского. Запишем определение этой размерности, убрав предел, его мы будем имитировать в итерациях, в которых будет изменяться размер ячеек.

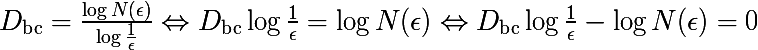
Если зафиксировать размеры ячеек ε и рассматривать D_bc как неизвестное, то легко заметить, что приведенное выражение является формулой линии. Мы можем запустить цикл по различным размерам ячеек ε и записывать результат. Давайте нанесем эти результаты на график и построим линию регрессии для полученного множества данных, это значение и будет являться аппроксимацией фрактальной размерности Минковского.

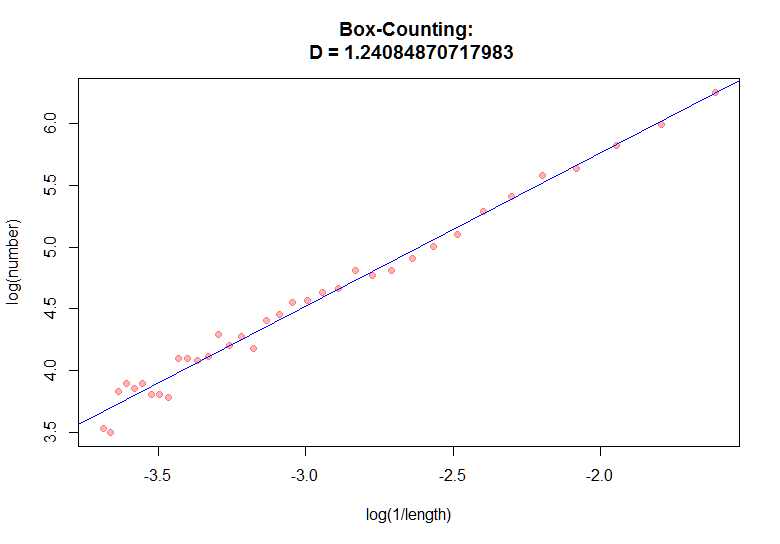
Вот кстати список объектов с их фрактальными размерностями.

Надеюсь у меня получилось передать связь между естественной размерностью, и тем каким образом и зачем люди пришли к другим определениям размерности. Давайте перейдем к коду, а затем к примерам.

Box-counting алгоритм, C# код

Для вычисления размерности Минковского нам необходимы будут две процедуры, начнем с линейной регрессии. Вообще решить задачу линейной регрессии можно различными способами, чаще всего для этого используется метод градиентного спуска и метод наименьших квадратов (Normal equations). Первый хорошо работает на больших и широких данных, второй слабоват на широких данных из-за необходимости вычислять обратную матрицу, ширина которой равна ширине массива данных. В нашем случае ширина всего 2, так что это наш случай. В векторизованном виде решение линейной регрессии записывается следующим образом:

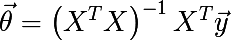
Обратную матрицу будем искать по следующей формуле:

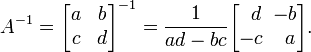
В нулевом элементе выходного вектора содержится угловой коэффициент (это и будет искомая размерность Минковского), а в следующем элементе — смещение. И собственно ключевая функция, которая возвращает датасет, по которому необходимо вычислить угловой коэффициен

Остается только связать две процедуры:

IDictionary<double, double> baList = BowCountingDimension(bwContour, 5, 100, 1, dir + "boxing\\");

double[] y = new double[baList.Count];

double[] x = new double[baList.Count];

int c = 0;

foreach (double key in baList.Keys)

{

y[c] = baList[key];

x[c] = key;

c++;

}

double[] theta = NormalEquations2d(y, x);

Примеры

Буква

Рассмотрим простое изображение без особенностей, т.е. с гладкими краями. В компьютерном зрении часто анализируется не изображение целиком, а его контур.

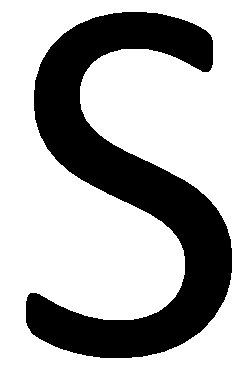
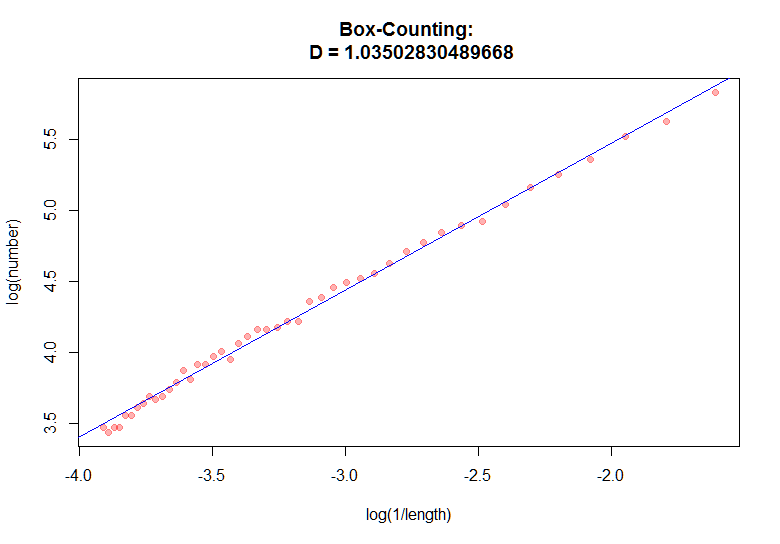
Фрактальная размерность в районе единицы сообщает нам о том, что фигура действительно без особенностей, и вполне гладкая.

http://habrahabr.ru/post/208368/

Приложение 1.

Классификация фракталов

Для чтобы представить все многообразие фракталов удобно прибегнуть к их общепринятой классификации.