Замкнутые системы массового обслуживания
До сих пор мы рассматривали системы, в которых входящий поток никак не связан с выходящим. Такие системы называются разомкнутыми. В некоторых же случаях обслуженные требования после задержки опять поступают на вход. Такие СМО называются замкнутыми.
Примеры:
· Поликлиника, обслуживающая данную территорию.
· Бригада рабочих, закрепленная за группой станков.
В замкнутых СМО циркулирует одно и то же конечное число потенциальных требований. Пока потенциальное требование не реализовалось в качестве требования на обслуживание, считается, что оно находится в блоке задержки.
В момент реализации оно поступает в саму систему. Например, рабочие обслуживают группу станков. Каждый станок является потенциальным требованием, превращаясь в реальное в момент своей поломки. Пока станок работает, он находится в блоке задержки, а с момента поломки до момента окончания ремонта – в самой системе. Каждый работник является каналом обслуживания.
Пусть n – число каналов обслуживания, s – число потенциальных заявок, 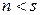 , λ –интенсивность потока заявок каждого потенциального требования, m – интенсивность обслуживания,
, λ –интенсивность потока заявок каждого потенциального требования, m – интенсивность обслуживания, 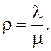 . Поток
. Поток
· Вероятность простоя (того, что все обслуживающие аппараты свободны, нет заявок):
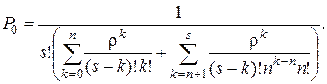 (4.27)
(4.27)
· Финальные вероятности состояний системы
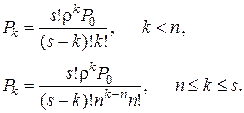 (4.28)
(4.28)
Через эти вероятности выражается среднее число замкнутых каналов:
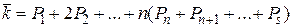 или
или
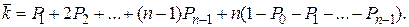 (4.29)
(4.29)
Через 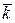 находим абсолютную пропускную способность системы
находим абсолютную пропускную способность системы
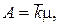 (4.30)
(4.30)
а также среднее число заявок в системе
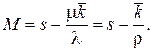 (4.31)
(4.31)
Дата добавления: 2020-10-14; просмотров: 585;











