Геометрические фракталы

Фракталы этого класса самые наглядные. В двухмерном случае их получают с помощью некоторой ломаной (или поверхности в трехмерном случае), называемой генератором. За один шаг алгоритма каждый из отрезков, составляющих ломаную, заменяется на ломаную-генератор, в соответствующем масштабе. В результате бесконечного повторения этой процедуры, получается геометрический фрактал.

ь
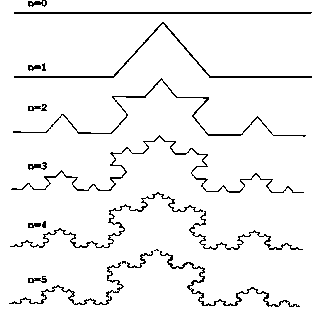
Рис 1. Построение триадной кривой Кох.

Рассмотрим один из таких фрактальных объектов - триадную кривую Кох [3]. Построение кривой начинается с отрезка единичной длины (рис.1) - это 0-е поколение кривой Кох. Далее каждое звено (в нулевом поколении один отрезок) заменяется на образующий элемент, обозначенный на рис.1 через n=1. В результате такой замены получается следующее поколение кривой Кох. В 1-ом поколении - это кривая из четырех прямолинейных звеньев, каждое длиной по 1/3. Для получения 3-го поколения проделываются те же действия - каждое звено заменяется на уменьшенный образующий элемент. Итак, для получения каждого последующего поколения, все звенья предыдущего поколения необходимо заменить уменьшенным образующим элементом. Кривая n-го поколения при любом конечном n называется предфракталом. На рис.1 представлены пять поколений кривой. При n стремящемся к бесконечности кривая Кох становится фрактальным обьектом [3].

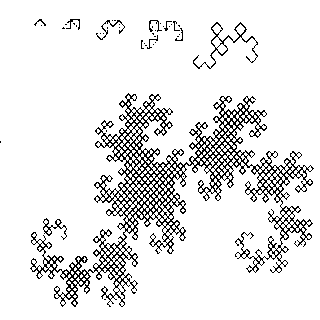
Рис 2. Построение "дракона" Хартера-Хейтуэя.

Для получения другого фрактального объекта нужно изменить правила построения. Пусть образующим элементом будут два равных отрезка, соединенных под прямым углом. В нулевом поколении заменим единичный отрезок на этот образующий элемент так, чтобы угол был сверху. Можно сказать, что при такой замене происходит смещение середины звена. При построении следующих поколений выполняется правило: самое первое слева звено заменяется на образующий элемент так, чтобы середина звена смещалась влево от направления движения, а при замене следующих звеньев, направления смещения середин отрезков должны чередоваться. На рис.2 представлены несколько первых поколений и 11-е поколение кривой, построенной по вышеописанному принципу. Предельная фрактальная кривая (при n стремящемся к бесконечности) называется драконом Хартера-Хейтуэя [3].

В машинной графике использование геометрических фракталов необходимо при получении изображений деревьев, кустов, береговой линии. Двухмерные геометрические фракталы используются для создания объемных текстур (рисунка на поверхности обьекта) [2,3].