Фракталы и системы счисления. Классические фракталы и методы их построения

Когда большинству людей казалось, что геометрия в природе ограничивается такими простыми фигурами, как линия, круг, коническое сечение, многоугольник, сфера, квадратичная поверхность, а также их комбинациями. К примеру, что может быть красивее утверждения о том, что планеты в нашей солнечной системе движутся вокруг солнца по эллиптическим орбитам?

Однако многие природные системы настолько сложны и нерегулярны, что использование только знакомых объектов классической геометрии для их моделирования представляется безнадежным. Как к примеру, построить модель горного хребта или кроны дерева в терминах геометрии? Как описать то многообразие биологических конфигураций, которое мы наблюдаем в мире растений и животных? Представьте себе всю сложность системы кровообращения, состоящей из множества капилляров и сосудов и доставляющей кровь к каждой клеточке человеческого тела. Представьте, как хитроумно устроены легкие и почки, напоминающие по структуре деревья с ветвистой кроной.

Столь же сложной и нерегулярной может быть и динамика реальных природных систем. Как подступиться к моделированию каскадных водопадов или турбулентных процессов, определяющих погоду?

Фракталы и математический хаос --- подходящие средства для исследования поставленных вопросов. Термин фрактал относится к некоторой статичной геометрической конфигурации, такой как мгновенный снимок водопада. Хаос --- термин динамики, используемый для описания явлений, подобных турбулентному поведению погоды. Нередко то, что мы наблюдаем в природе, интригует нас бесконечным повторением одного и того же узора, увеличенного или уменьшенного во сколько угодно раз. Например, у дерева есть ветви. На этих ветвях есть ветки поменьше и т.д. Теоретически, элемент «разветвление» повторяется бесконечно много раз, становясь все меньше и меньше. То же самое можно заметить, разглядывая фотографию горного рельефа. Попробуйте немного приблизить изображение горной гряды --- вы снова увидите горы. Так проявляется характерное для фракталов свойство самоподобия.

Во многих работах по фракталам самоподобие используется в качестве определяющего свойства. Следуя Бенуа Мадельброту, мы принимаем точку зрения, согласно которой фракталы должны определяться в терминах фрактальной (дробной) размерности. Отсюда и происхождение слова фрактал (от лат. fractus --- дробный).

Понятие дробной размерности представляет собой сложную концепцию, которая излагается в несколько этапов. Прямая --- это одномерный объект, а плоскость --- двумерный. Если хорошенько перекрутив прямую и плоскость, можно повысить размерность полученной конфигурации; при этом новая размерность обычно будет дробной в некотором смысле, который нам предстоит уточнить. Связь дробной размерности и самоподобия состоит в том, что с помощью самоподобия можно сконструировать множество дробной размерности наиболее простым образом. Даже в случае гораздо более сложных фракталов, таких как граница множества Мандельброта, когда чистое самоподобие отсутствует, имеется почти полное повторение базовой формы во все более и более уменьшенном виде.

Фрактал (лат. fractus — дробленый) — термин, означающий геометрическую фигуру, обладающую свойством

самоподобия, то есть составленную из нескольких частей, каждая из которых подобна всей фигуре целиком. В более широком смысле под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, строго большую топологической.

Следует отметить, что слово «фрактал» не является математическим термином и не имеет общепринятого строгого математического определения. Оно может употребляться, когда рассматриваемая фигура обладает какими-либо из перечисленных ниже свойств:

Обладает нетривиальной структурой на всех шкалах. В этом отличие от регулярных фигур (таких, как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень крупном масштабе, он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, на всех шкалах мы увидим одинаково сложную картину.

Является самоподобной или приближённо самоподобной.

Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.

Может быть построена при помощи рекурсивной процедуры.

Многие объекты в природе обладают фрактальными свойствами, например, побережья, облака, кроны деревьев, кровеносная система и система альвеол человека или животных.

Фракталы, особенно на плоскости, популярны благодаря сочетанию красоты с простотой построения при помощи компьютера.

Одним из первых описал динамические фракталы в 1918 году французский математик Гастон Жюлиа в своем объемном труде в несколько сотен страниц. Но в нем отсутствовали какие-либо изображения. Компьютеры сделали видимым то, что не могло быть изображено во времена Жюлиа. Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке (например, множество Кантора). Термин «фрактал» был введён Бенуа Мандельбротом в 1975 году и получил широкую популярность с выходом в 1977 году его книги «Фрактальная геометрия природы».

Квазифрактал отличается от идеальных абстрактных фракталов неполнотой и неточностью повторений структуры. Большинство встречающихся в природе фракталоподобных структур (границы облаков, линия берега, деревья, листья растений, кораллы, …) являются квазифракталами, поскольку на некотором малом масштабе фрактальная структура исчезает. Природные структуры не могут быть идеальными фракталами из-за ограничений, накладываемых размерами живой клетки и, в конечном итоге, размерами молекул.

Мультифрактал — комплексный фрактал, который может детерминироваться не одним единственным алгоритмом построения, а несколькими последовательно сменяющими друг друга алгоритмами. Каждый из них генерирует паттерн со своей фрактальной размерностью. Для описания мультифрактала вычисляют мультифрактальный спектр, включающий в себя ряд фрактальных размерностей присущих элементам данного мультифрактала.

Предфрактал — это самоподобная геометрическая фигура, каждый фрагмент которой повторяется в упрощённом виде при уменьшении масштаба в конечное число раз. Количество уровней масштаба, на которых наблюдается подобие, называется порядком предфрактала. При порядке, стремящемся к бесконечности, предфрактал переходит во фрактал.

Фракта́л (лат. fractus — дроблёный, сломанный, разбитый) — математическое множество, обладающее свойством самоподобия, то есть однородности в различных шкалах измерения. В математике под фракталами понимают множества точек в евклидовом пространстве, имеющие дробную метрическую размерность (в смысле Минковского или Хаусдорфа), либо метрическую размерность, отличную оттопологической, поэтому их следует отличать от прочих геометрических фигур, ограниченных конечным числом звеньев.

Первые примеры самоподобных множеств с необычными свойствами появились в XIX веке в результате изучения непрерывных недифференциируемых функций (например, функция Больцано, функция Вейерштрасса, множество Кантора). Термин «фрактал» введён Бенуа Мандельбротом в 1975 году и получил широкую известность с выходом в 1977 году его книги «Фрактальная геометрия природы». Особую популярность фракталы обрели с развитием компьютерных технологий, позволивших эффектно визуализировать эти структуры.

Слово «фрактал» употребляется не только в качестве математического термина. Фракталом может называться предмет, обладающий, по крайней мере, одним из указанных ниже свойств:

· Обладает нетривиальной структурой на всех масштабах. В этом отличие от регулярных фигур (таких как окружность, эллипс, график гладкой функции): если мы рассмотрим небольшой фрагмент регулярной фигуры в очень при очень крупном масштабе, то он будет похож на фрагмент прямой. Для фрактала увеличение масштаба не ведёт к упрощению структуры, то есть на всех шкалах мы увидим одинаково сложную картину.

· Является самоподобным или приближённо самоподобным.

· Обладает дробной метрической размерностью или метрической размерностью, превосходящей топологическую.

Многие объекты в природе обладают свойствами фрактала, например: побережья, облака, кроны деревьев, снежинки, кровеносная система, система альвеол человека или животных.

Фракталы быстро стали популярны, не в последнюю очередь благодаря красочным компьютерным иллюстрациям, рис.1 (Мандельброт был сотрудником корпорации IBM).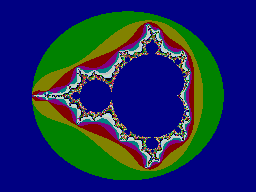

Рис.1 Фрактал Мандельброта

Внимательное изучение фракталов привело к пониманию, что они существовали и были известны ученым (Пуанкаре, Фату, Жюлиа, Кантор, Хаусдорф) и до Мандельброта, и заслуга последнего состояла скорее в привлечении внимания к этим структурам и указании на чрезвычайно широкое распространение фрактальных объектов в нашем мире.

Из рукотворных, математических фракталов известны кривая или снежинка Гельги фон Кох (рис.2, 3), треугольник Серпинского (рис.4), и другие (рис.5), строящиеся с помощью некоторого алгоритма, примененного к кривой или поверхности.

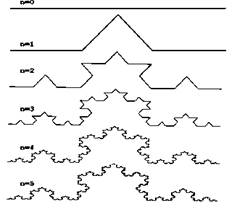
Рис.2. Снежинка Кох. Рис.3. Построение кривой Кох.

Для таких кривых (рис.2-5) часть рисунка n-ной итерации будет в точности тождественна части (n-1)-ой итерации большего размера.

Рисунки, подобные рис.1, изображают области притяжения к различным точкам, аттракторам, в пространстве системы нелинейных уравнений. Различные области отражаются на картинке разными цветами. Система нелинейных уравнений могут характеризоваться чрезвычайной чувствительностью к малейшим изменениям параметров системы, в результате чего сколь угодно близкие на фазовом пространстве точки могут в конечном итоге стремиться к различным аттракторам. Что означает, что увеличение масштаба изображения не приведет к упрощенной его версии, а только к появлению картинки, подобной исходной. В этих случаях речь идет именно о подобии, а не о точном тождественном воспроизведении.

Именно фракталы этого типа являются визитной карточкой Мандельброта. Причем свойство фрактальности, то есть схожести структур целого фазового пространства и его части, повторяется бесконечное количество увеличений масштаба – маленький кусочек исходной картинки при увеличении выглядит аналогично всей картинке, вырезанный кусочек из этой маленькой картинки при увеличении выглядит аналогично его предшественнику, и так далее.

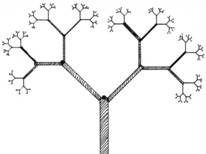
Рис.4. Треугольник Серпинского. Рис.5. Ветвящееся дерево.

И эти сложные математические объекты, создание которых невозможно без помощи компьютера, привлекают неизменный интерес как математиков, так и людей, чрезвычайно от нее далеких, привлекают своей завораживающей и повторяющейся красотой, подобной очарованию сменяющих друг друга картинок в детском калейдоскопе. Сходные последовательные изображения погружают зрителя в волшебный ирреальный мир, кружит голову идеей бесконечного повторения, тождества и подобия, повторения в масшабе ,пространстве и времени.

Быстро было обнаружено множество природных объектов, строение которых сходно с фракталами – это и ветки деревьев, повторяющие более крупные ветви, повторяющие ствол, и снежинки, и кровеносные пути и нервы, разветвляющиеся на более мелкие пути, которые ветвятся на еще более мелкие, и карта мозговых полушарий, да и любая карта, при увеличении масштаба превращающаяся в иную карту, фрагмент которой при следующем увеличении есть еще одна схожая карта, и т.д.

Похоже, что весь окружающий мир, за редкими бессмысленными исключениями, представляет собой фракталы.

Рис. 6. Фрактальный лес (из книги Michael Barnsley. Fractals everywhere. Boston: Academic Press, 1988)