Контура управления самонаводящимся снарядом

Система наведения снаряда является замкнутой системой автоматического управления. Она решает две основные задачи: на основе информации о координатах и параметрах движения цели определяет траекторию движения центра масс ракеты и обеспечивает ее полет по этой траектории путем изменения величины нормальных управляющих сил. В контур этой системы (в контур управления) в качестве одного из звеньев входит система стабилизации, предназначенная для сохранения требуемого углового положения или установившегося углового движения ракеты. Объектом управления системы стабилизации и системы наведения в целом является ракета. Контур управления замыкается через так называемое кинематическое звено, устанавливающее связь между движением ракеты и движением цели.

Структурная схема кинематического звена определяется выбранным методом наведения и параметром рассогласования.
Структурная схема и параметры контура управления должны обеспечивать заданную точность наведения ракеты на цель при условии, когда входные сигналы кроме регулярных воздействий, обусловленных движением цели, а также продольным движением ракеты, имеют в своем составе относительно высокий уровень случайных возмущений.
Чтобы иметь представление о том, насколько контур управления полетом ракеты удовлетворяет требованиям по устойчивости, качеству переходного процесса и точности наведения ракеты (при известных сигналах управления и помехи), необходимо знать передаточные функции контура управления и его амплитудно-частотные характеристики.
Для получения аналитического выражения передаточной функции контура управления необходимо располагать математическим описанием физических звеньев, входящих в контур управления, и связями между ними.
Для построения структурных схем необходимо иметь также математическое описание процесса управления ракетой, выражаемое системой уравнений. Работа контура управления полетом ракеты в общем случае описывается системой нелинейных дифференциальных уравнений; уравнения ракеты, характеризующие связи между ее выходными параметрами (углом наклона вектора линейной скорости ракеты , углом наклона продольной оси ракеты , нормальным ускорением и углами отклонения рулей ракеты.
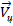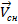Скорость сближения снаряда и цели определяется с помощью проекции векторов и на линию визирования 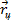соотношением

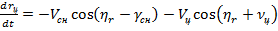. (7.14)

Геометрические соотношения приняты те же, что и на рисунке 7.3, но для лучшего понимания повторим их. Кроме того, введем угловое положение вектора скорости цели .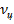

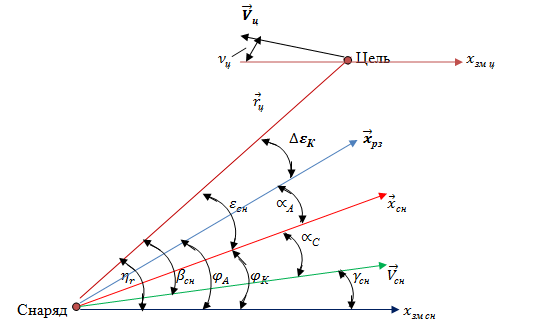
Рисунок 7.11 – Геометрические соотношения при

самонаведении на движущуюся цель

Линейная скорость вращения линии визирования 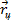определяется через проекци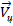и и 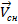на нормаль к 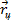, так что

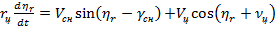. (7.15)

Соотношения (7.14) и (7.15) являются кинематическими уравнениями, отображающими математическую связь между выходной величиной звена Автопилот-Снаряд (углом 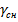), внешним динамическим воздействием на систему управления (углом 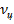) и угловой скоростью вращения линии визирования 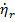, которая измеряется головкой СН.

Проведем рассмотрение для случая наведения на встречных курсах, в условиях, когда углы 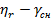и 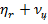– можно считать малыми, что позволяет линеаризировать уравнения (7.14) и (7.15). В этом случае уравнения упрощаются и принимают вид

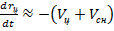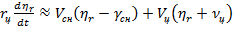, . (7.16)

Преобразовав последние соотношения, получаем

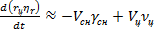. (7.17)

Это равенство в операторной форме записывается следующим образом

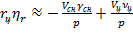. (7.18)

Оно определяет структурную схему кинематического звена для рассматриваемого случая самонаведения (рисунок 7.12).

Если совместить ось координат 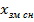(рисунок 7.11) с линией визирования цели 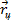в момент 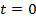, то величины

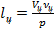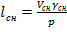; (7.19) будут представлять собой отклонения цели и снаряда от первоначального положения линии визирования цели (рисунок 7.12), а 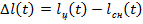разность линейных отклонений.

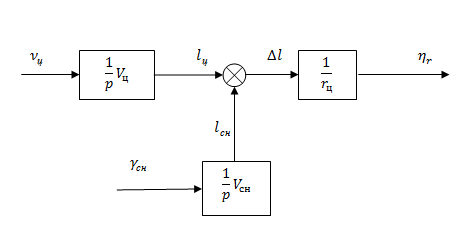
Рисунок 7.12 – Структурная схема кинематического звена

При этом в момент пролета снаряда на кратчайшем расстоянии от цели 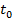разность линейных отклонений от первоначальной линии визирования 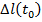определит промах снаряда .

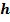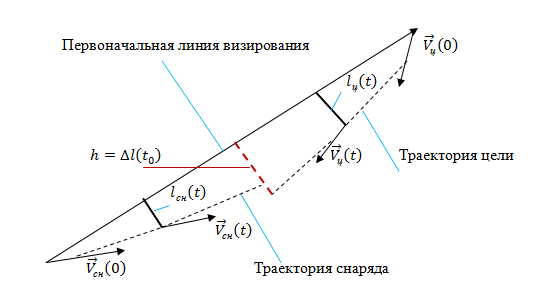
Рисунок 7.13 – Траектория движения снаряда и цели

Структурная схема кинематического звена на рисунке 7.12 может быть непосредственно использована в случае головки СН со следящим гироприводом, когда входной величиной является угол 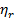(рисунок 7.8).

В случае, когда на структурной схеме головки СН имеется угол между осью снаряда и направлением на цель 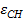(рисунки 7.6 и 7.7), схему на рисунке 7.12 следует дополнить разностным звеном для получения угла .

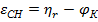Структурные схемы контуров СН получаются путем комбинации структурных схем кинематического звена, головки СН и звена Автопилот-Снаряд.

Рассмотрим структурную схему контура прямого СН на неподвижную цель (рисунок 7.14). Так как скорость цели равна нулю, то вместо (7.18) имеем

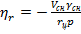, поэтому структурная схема кинематического звена на рисунке 7.14 упрощается по сравнению со структурной схемой этого звена, приведенной на рисунке 7.12. Инерционностью головки СН, неподвижно укрепленной на корпусе снаряда, можно пренебречь. Тогда головка изображается безынерционным звеном с коэффициентом передачи 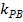. Сигнал рассогласования с головки СН поступает на устройство формирования команды с передаточной функцией .

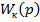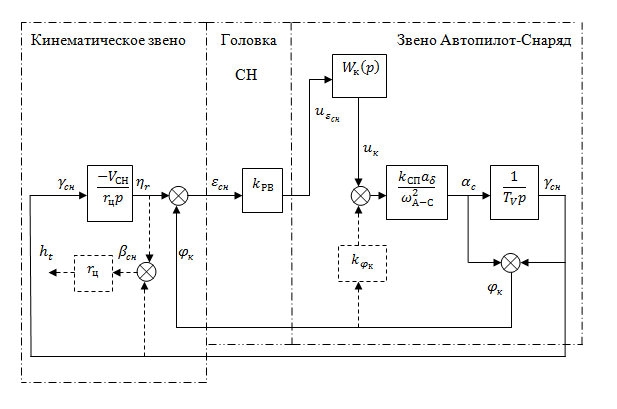
Рисунок 7.14 – Структурная схема контура прямого самонаведения

Устройство формирования команды предназначено для функционального преобразования командного сигнала. Так, например, для повышения порядка астатизма системы управления в устройстве формирования команды в командный сигнал может добавляться интеграл, а для обеспечения устойчивости – производные этого сигнала и т.д. Обратная связь с помощью позиционного гироскопического датчика с коэффициентом передачи 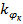показана в схеме звена Автопилот-Снаряд пунктиром, так как она применяется не всегда.

Для характеристики точности работы системы СН введем понятие текущего промаха 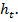В случае неподвижной цели при малой угловой ошибке наведения снаряда на цель 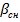текущий промах определяется следующим приближенным равенством

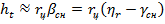. (7.20)

В соответствии с этим равенством кинематическое звено в структурной схеме на рисунке 7.14 дополнено связями (пунктиром) для получения текущего промаха.

Рассмотрим структурную схему контура самонаведения методом пропорционального сближения при головке СН со следящим гироприводом.

Кинематическое звено здесь соответствует схеме на рисунке 7.12. Инерционностью внутреннего контура головки СН пренебрегаем, поэтому используем приближенную передаточную функцию (7.12) вместо точной (7.11). Звено Автопилот-Снаряд на схеме то же, что и на рисунке 7.14.

В случае подвижной цели текущий промах выражается формулой

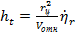. (7.21)

Здесь 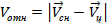– модуль относительной скорости сближения снаряда и цели. Кинематическое звено в соответствии с (7.21) дополнено (пунктиром) цепочкой для получения текущего промаха .

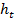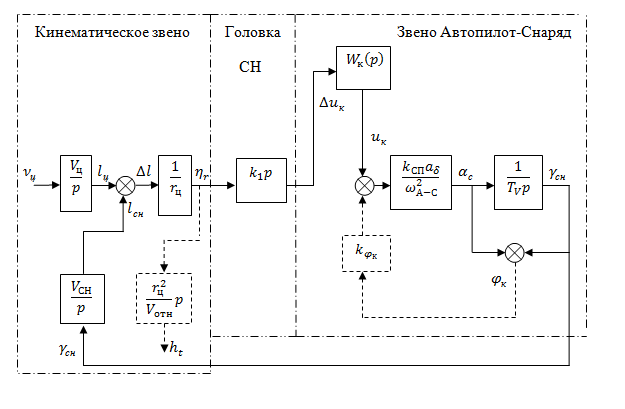
Рисунок 7.15 – Структурная схема контура самонаведения методом пропорционального сближения (головка СН со следящим гироприводом)

Точность наведения ракеты на цель зависит от параметров движения цели, характеристик и инструментальной точности работы звеньев, входящих в состав контура управления, и возникающих внутри контура паразитных возмущений. Она может быть определена путем решения полной системы дифференциальных уравнений с переменными коэффициентами, описывающих поведение системы управления при входном воздействии, имеющем регулярную и случайную составляющие.

В инженерной практике находят применение приближенные методы анализа системы управления при следующих допущениях: неустановившееся возмущенное движение ракеты отличается от исходного установившегося лишь малым отклонением параметров движения, что позволяет свести нелинейные дифференциальные уравнения к линейным; «замораживаются» переменные коэффициенты дифференциальных уравнений системы управления.
Введение допущений позволяет для оценки качества функционирования контура управления полетом ракеты применять использованный нами метод передаточных функций или частотный метод.