Амплитудно-модулированный сигнал
Рассмотрим простейший случай амплитудно-модулированного (AM) сигнала A(t):

(3.45)
Здесь ω0 – частота несущей, Ω – частота модуляции, m – коэффициент модуляции. Обычно m < 1. АМ сигнал представляет собой просто сумму трёх спектральных составляющих. На рис. 3.26 представлен спектр такого АМ сигнала, состоящий из трёх частот. Там же представлена векторная диаграмма (справа).
 Рис. 3.26.
Рис. 3.26.
Спектральные составляющие АМ сигнала (слева). Векторная диаграмма АМ сигнала (справа).
Относительно вектора основного колебания гармоники вращаются с частотами ± Ω.
Вектор А(t) на рис. 3.26 не стоит на месте, а вращается с круговой частотой ω0 радиан в секунду. А маленькие векторчики mA/2тоже вращаются. Один немного медленнее, другой – немного быстрее с частотами ω0 +Ω и ω0 – Ω. Их сумма всегда совпадает по направлению с вектором А. Поэтому длина вектора А, то есть амплитуда сигнала, меняется с частотой Ω (см. рис. 3.26). Если перейти к комплексной зависимости от времени eiωt , то при t = 0 A(t) будет вещественным (см. (3.45)) и все три вектора будут вращаться против часовой стрелки, но с разными частотами.
Если заметить, что максимальная амплитуда будет AMAX = A(1 + m), а минимальная будет
AMIN = A(1 – m), то можно вычислить, что 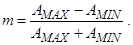
Модулирующее напряжение, как правило, несинусоидальное. Можно показать, как спектр АМ сигнала UAM (ω) связан со спектром амплитудной огибающей модулирующего напряжения ASLOW (ω) (см. теорему о переносе спектра, (3.30)).

Здесь ω0 – несущая частота. (3.46)
Это и проиллюстрировано графиками на рис. 3.27.

Рис. 3.27.
Связь спектра огибающей и спектра АМ сигнала (теорема о переносе спектра).
Если взять меандр, то есть прямоугольные импульсы, как на рис. 3.9 и промодулировать ими синусоидальный сигнал несущей частоты, то получится спектр, похожий на спектр рис. 3.27, но с другой огибающей.

Рис. 3.28.
Несущая промодулирована прямоугольными импульсами.
Дата добавления: 2017-10-04; просмотров: 1405;











