Основы теории гидродинамических передач

Кинематика потока

Рабочие колеса представляют собой вращающиеся решетки лопаток. Принимая условно, что в колесе находится бесконечно большое число бесконечно тонких лопаток, можно считать, что поток в колесе разбит на отдельные элементарные струйки, форма которых определяется конфигурацией межлопастных каналов. Это дает возможность применить к теории гидродинамических передач струйную модель потока.

Допустим, что в рабочих колесах отсутствуют потери напора и утечки, т. е. преобразование энергии происходит без потерь. Такую гидропередачу называют теоретической. Проходя через рабочее колесо (рис. 4.5), частицы жидкости совершают сложное движение: переносное (вместе с лопатками колеса) с окружной скоростью u = ωR, которая направлена по нормали к радиусу R, и u = ωR относительное (относительно лопаток колеса) со скоростью ω, которая направлена по касательной к профилю лопатки.

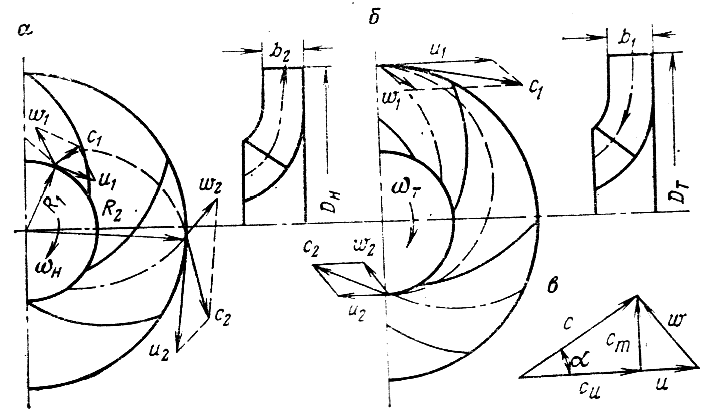
Рисунок 4.5 – Схемы рабочих колес и параллелограммы скоростей

Абсолютная скорость движения любой частицы жидкости с равна геометрической сумме составляющих, т. е. 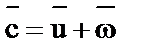. Спроектировав скорость с на радиальное и тангенциальное направления, получим ее составляющие: меридиональную скорость с_т и скорость закручивания с_и (рис. 4.5, в).

В качестве примера рассмотрим кинематику потока в наиболее распространенных для гидродинамических передач типах колес: центробежном колесе насоса (см. рис. 4.5, а) и центростремительном (радиально-осевом) колесе турбины (см. рис. 4.5, б). На указанных рисунках приведены схемы этих колес и параллелограммы скоростей, а также показана (пунктиром) траектория движения одной из частиц жидкости, движущейся с абсолютной скоростью с.

Уравнения моментов

При выводе уравнений моментов используется теорема об изменении момента количества движения, согласно которой момент внешних сил, приложенных к колесу равен изменению момента количества движения, протекающей через него жидкости.

Для насосного колеса гидродинамической передачи это будет:

М_н = К_н2 – К_н1 = ρQ_тС_и2R₂ – ρQ_тС_и2R₁, (4.1)

где М_н – момент на валу насосного колеса; К_н2; К_н1 – моменты количества движения жидкости на выходе (К_н2) и входе (К_н1) насосного колеса; Q_т – теоретический расход жидкости через колесо; R₂, R₁ – выходной и входной радиусы (рис. 4.5); ρ – плотность жидкости; С_и2, С_и1 – скорости закручивания на выходе и входе колеса.

Таким образом, действующий на вал насосного колеса момент увеличивает момент количества движения массовой подачи жидкости. Как видно из уравнения (4.1), вращающий момент обуславливается плотностью жидкости, теоретической подачей и значениями величин радиусов и скоростей закручивания в выходном и входном сечениях колеса.

Действительный момент на ведущем валу будет больше теоретического из-за гидравлических и механических потерь с насосе.

В турбинном колесе момент количества движения массового расхода жидкости, протекающей через колесо, уменьшается, так как поток приводит колесо во вращение и создает теоретический крутящий момент на ведомом валу

М_т = М_т1 – М_т2 = ρQ_т(R₁c_и1 – R₂c_и2). (4.2)

Действительный момент на ведомом валу будет меньше М_т из-за гидравлических и механических потерь.

В реакторе момент количества движения (М_р.т) массового расхода жидкости может уменьшаться или увеличиваться в зависимости от соотношения между моментами М_н и М_т.

Поэтому

М_р.т = ρQ_р.т(R₁c_u1 ± R₂c_u2) (4.3)

В уравнениях (4.1) – (4.3) Q_н.т = Q_т.т = Q_р.т = Q_т.

Уравнения расхода (подачи) и напоров

Исходя из уравнения расхода и в соответствии с кинематикой скоростей в рабочем колесе (см. рис. 4.5, б), теоретический расход турбины

Q_{т. т} = πD₁b₁c_m1k_c1, (4.4)

где k_c1 – коэффициент стеснения потока лопастями колеса.

Соответственно теоретическая подача насоса

Q_{н. т} = πD₂b₂c_m2k_c2. (4.5)

Реальная величина Q_н будет меньше, а Q_т больше определяемых уравнениями (4.4) и (4.5) из-за утечек в проточной части гидропередачи.

При отсутствии потерь энергии в насосном колесе его теоретический напор можно определить, приравняв значение мощности на ведущем валу N_{н. т} к значению мощности потока жидкости, протекающей в колесе N_{н. вн}, т. е. N_{н. т} = N_{н. вн}.:

N_{н. т} = ω_нМ_{н. т} = ω_нρQ_{н. т} (R₂c_u2 – R₁c_u1). (4.6)

Так как ωR = u, то N_{н. т} = ρQ_{н. т} (u₂c_u2 – u₁c_u1). Мощность потока

N_{н. вн} = ρgH _{н. т} Q_{н. т}. (4.7)

Решая совместно уравнения N_{н. т} и N_{н. вн} относительно H _{н. т}, получим

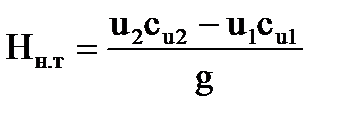(4.8)

Для турбинного колеса соответственно

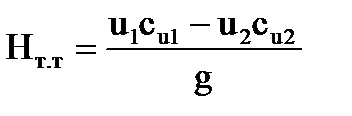(4.9)

Это уравнение впервые было получено в 1754 г. академиком Л. Эйлером и называется его именем (турбинное уравнение Эйлера).

Действительное значение Н_н будет меньше, а Н_т больше определяемых уравнениями из-за потерь напора и наличия вихрей в межлопостных каналах колес [19].

Напор в реакторе в отличии от момента не меняется (если пренебречь потерями), т. е. реактор может изменять только момент количества движения жидкости, не изменяя мощности потока.

Как видно из уравнений, напор в разных точках меридиального сечения будет различным. Изменение статического напора в рабочих колесах, а следовательно, и давление прямопропорционально изменению полного напора. Вследствие этого давление будет наименьшим при входе в насосное колесо и максимальным на выходе из него. Поэтому подвод рабочей жидкости к рабочей полости (питании) осуществляется как можно ближе к оси вращения колес, а отвод ее – на максимальном радиусе. По этой же причине кавитация в гидропередаче появляется прежде всего на минимальном радиусе колеса.

Из-за неравенства площадей проекций дисков рабочих колес на плоскость, перпендикулярную к оси вращения, неравномерности распределения давлений по меридиальному сечению и неравенства динамических сил от натекания жидкости на диски рабочих колес в гидродинамических передачах возникают осевые усилия. Величина их зависит от величины неуравновешенной площади, рабочего режима гидропередачи, давления подпитки и плотности жидкости [3]. Для восприятия осевых сил в гидродинамических передачах предусматриваются соответствующие подшипники.

Основы подобия

Исходя из общих условий подобия движения жидкости, лопастные машины можно считать полностью подобными, если будет соблюдаться геометрическое, кинематическое и динамическое подобие.

Геометрическое подобие характеризуется равенством отношений всех сходственных геометрических размеров рассматриваемых машин, включая величины шероховатости поверхностей и зазоров.

Кинематическое подобие заключается в постоянстве отношений скоростей в сходственных точках геометрически подобных машин (в частности, треугольников скоростей).

Динамическое подобие выражается постоянством отношений сил одинаковой природы, действующих в сходственных точках в кинематически подобных машинах. В гидродинамических передачах основными являются силы инерции, давления и трения. Как известно, критериями подобия в этом случае будут числа Эйлера и Рейнольдса [3]. Если течение жидкости в проточной части машин находится в области автомодельности, то для соблюдения подобия достаточно сохранения постоянным числа Эйлера.

Для подобных гидродинамических машин основными являются уравнения подобия, связывающие между собой диаметры (D₁, D₂); частоты вращений колес (n₁, n₂); расхода жидкости (Q₁, Q₂); напоры (Н₁, Н₂); мощности (N₁, N₂); плотности (ρ₁, ρ₂) и моменты (М₁, М₂). Эти уравнения имеют вид:

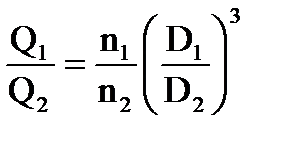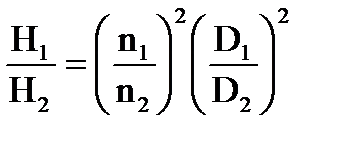; ; (4.10;4.11)

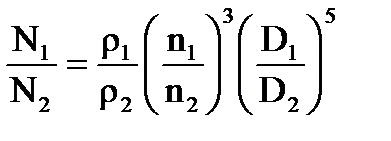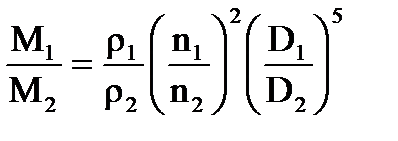; (4.12;4.13)

Для одной и той же лопастной машины или гидродинамической передачи (D₁ = D₂), работающей на одной и той же жидкости (ρ₁ = ρ₂) в автомодельном режиме, уравнения пересчета будут

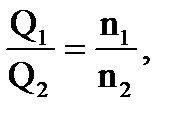
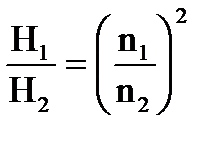; (4.14;4.15)

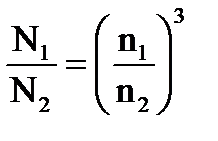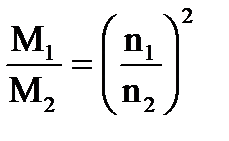, . (4.16;4.17)

Если мощности N₁ и N₂ выразить как N₁ = ρ₁gH₁Q₁η₁, N₂ = ρ₂gH₂Q₂η₂, то при η₁ = η₂ получим:

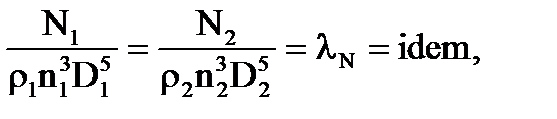(4.18)

откуда

N = λ_Nρn³D⁵, (4.19)

где λ_N – коэффициент мощности.

Аналогично получим формулу для момента:

N = λ_Мρn³D⁵, (4.20)

где λ_М – коэффициент момента.

Уравнения пересчета основных технических показателей подобных машин имеют очень большое значение. Зная их, можно решить задачу, как изменятся показатели гидропередачи с изменением частоты вращения колес, и наоборот, какую нужно дать частоту вращения колесам, чтобы получить необходимые технические показатели.